Контрольная работа по теории вероятностей. Контрольнаяработ а по предмету Теория вероятностей
 Скачать 163.5 Kb. Скачать 163.5 Kb.
|
К О Н Т Р О Л Ь Н А Я Р А Б О Т АПо предмету: Теория вероятностей.Вариант № 2.Выполнил: Студент 1 курса, 2 семестра Задание №1. Условие: В ящике 2 белых и 4 чёрных шара. Один за другим вынимаются все имеющиеся в нём шары. Найти вероятность того, что последний шар будет чёрным. Решение: Искомая вероятность равна вероятности того, что выбранный на удачу шар окажется черным эта вероятность равна Р(А) = 4/6 = 2/3 Ответ: 2/3 Задание №2. Условие: В партии товара, состоящей из 30 мужских пальто, находится 20 изделий местного производства. Товаровед наудачу выбирает 3 изделия. Какова вероятность того, что все 3 изделия окажутся: а) местного производства; б) не местного производства. Решение: Воспользуемся классическим определением вероятности. Классическая схема является математической формализацией опытов, в которых элементарные исходы обладают определенной симметрией по отношению к условию опыта, так что нет оснований считать какой-либо исходов более вероятным, чем другой. Если существует n – равно вероятных исходов, при этом m – из них благоприятствуют событию А, то вероятность события А найдется по формуле Р(А) = m/n. Найдем число всех исходов, оно равно числу сочетаний из 30 по 3. 14 10 30 30! С   = = = 4060. = = = 4060.3 Найдем число событий благоприятствующих событию а). Оно равно числу сочетаний из 20 по 3. 6 10 20 20! С   = = = 1140. = = = 1140.3 3! 17! 1 Тогда Р(А) = 1140 : 4060 = 0,28 – вероятность того, что изделия окажутся местного производства. Найдем число событий благоприятствующих событию б). Оно равно числу сочетаний из 10 по 3. 3 5 10 10! 8 С   = = = 120. = = = 120.3 3! 7! 1 Тогда Р(В) = 120 : 4060 = 0,03 – вероятность того, что все изделия окажутся не местного производства. Ответ: а). 0,28. б). 0,03. Задание №3. Условие: Статистика запросов кредитов в банке такова: 10% - государственные органы, 30% - другие банки, остальные - физические лица. Вероятности невозврата взятого кредита соответственно таковы: 0,01, 0,05 и 0,2. Найти вероятность невозврата очередного запроса на кредит. Начальнику кредитного отдела доложили, что получено сообщение о невозврате кредита, но в факсимильном сообщении имя клиента было неразборчиво. Какова вероятность, что данный кредит не возвращает какой-то банк? Решение: Найдем вероятности следующих событий: Р(А1) = 0,1 – вероятность того, что запрос на кредит от гос.органа. Р(А2) = 0,3 – вероятность того, что запрос на кредит от банка. Р(А3) = 0,6 – вероятность того, что запрос на кредит от физического лица. Р(В/А1) = 0,01 – вероятность невозврата кредита при условии, что он выдан государственному учреждению. Р(В/А2) = 0,05 – вероятность невозврата кредита при условии, что он выдан банку. Р(В/А3) = 0,2 – вероятность невозврата кредита при условии, что он выдан физическому лицу. Тогда вероятность невозврата кредита найдем по формуле полной вероятности. Р(В) = ∑ Р (В/Аi) Р (Аi) Р(В) = 0,1 . 0,01 + 0,3 . 0,05 + 0,6 . 0,2 = 0,001 + 0,015 + 0,12 = 0,136 Вероятность того, что невозвращенный кредит выдан банку найдем по формуле Байеса. Р(В/Аi) . Р(Аi) Р  (Аi/В) = = 0,015 / 0,136 = 0,11. (Аi/В) = = 0,015 / 0,136 = 0,11.∑ Р(В/Аi) . Р(Аi) Ответ: 0,136; 0,11. Задание №4. Условие: Какова вероятность выпадения хотя бы двух шестёрок при трёх бросаниях игральной кости? Решение: Воспользуемся схемой Бернулли. В теории вероятностей имеет большое значение простая схема случайных экспериментов, называемая схемой Бернулли. Испытаниями Бернулли называются независимые испытания с двумя исходами и с вероятностью успеха не меняющейся от испытания к испытанию. Вероятность Рn(m) – получить в m испытаниях равно n успехов находится по формуле: Рn(m) = Cnm Pm qn-m , (m = 0,1,2,...,n) таким образом: Р(А1) = С13 (1/6)1 . (5/6)2 = 3!/2! . 25/216 = 0,347 - это вероятность того, что из трех бросаний один раз выпадет шесть очков. Р(А2) = С23 (1/6)2 . (5/6)1 = 3!/2! . 5/216 = 0,069 Тогда искомая вероятность будет найдена как сумма выше вычисленных вероятностей. Р(А) = Р(А1) + Р(А2) = 0,347 + 0,069 = 0,416 Ответ: 0,416. Задание №5. Условие: Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженых семян: а) прорастёт ровно 700; б) число проросших заключено между 790 и 830. Решение: Если в схеме Бернулли, наряду с числом испытаний n «велики» также значения np и nq, то следует применять формулы Муавра-Лапласа – локальную или интегральную. При этом локальную формулу Муавра-Лапласа, как следует из самого названия, следует применять в том случае, когда нас интересует вероятность получить ровно m успехов в n испытаниях, а интегральную – если определяется вероятность получить число успехов заключенное в пределах от m1 до m2. а). Воспользуемся локальной теоремой Муавра-Лапласа. Если в схеме Бернулли число n «велико», то для всех m справедливо привлеченная формула (локальная формула Муавра-Лапласа). Где По условию задачи: n = 900, m = 700, p = 0,9, q = 0,1. Таким образом: φ(х) = φ(-х) φ(-12,22) = φ(12,22) = 0,0001 б). Воспользуемся интегральной теоремой Муавра-Лапласа. Если в схеме Бернулли число испытаний n «велико», то для вероятности 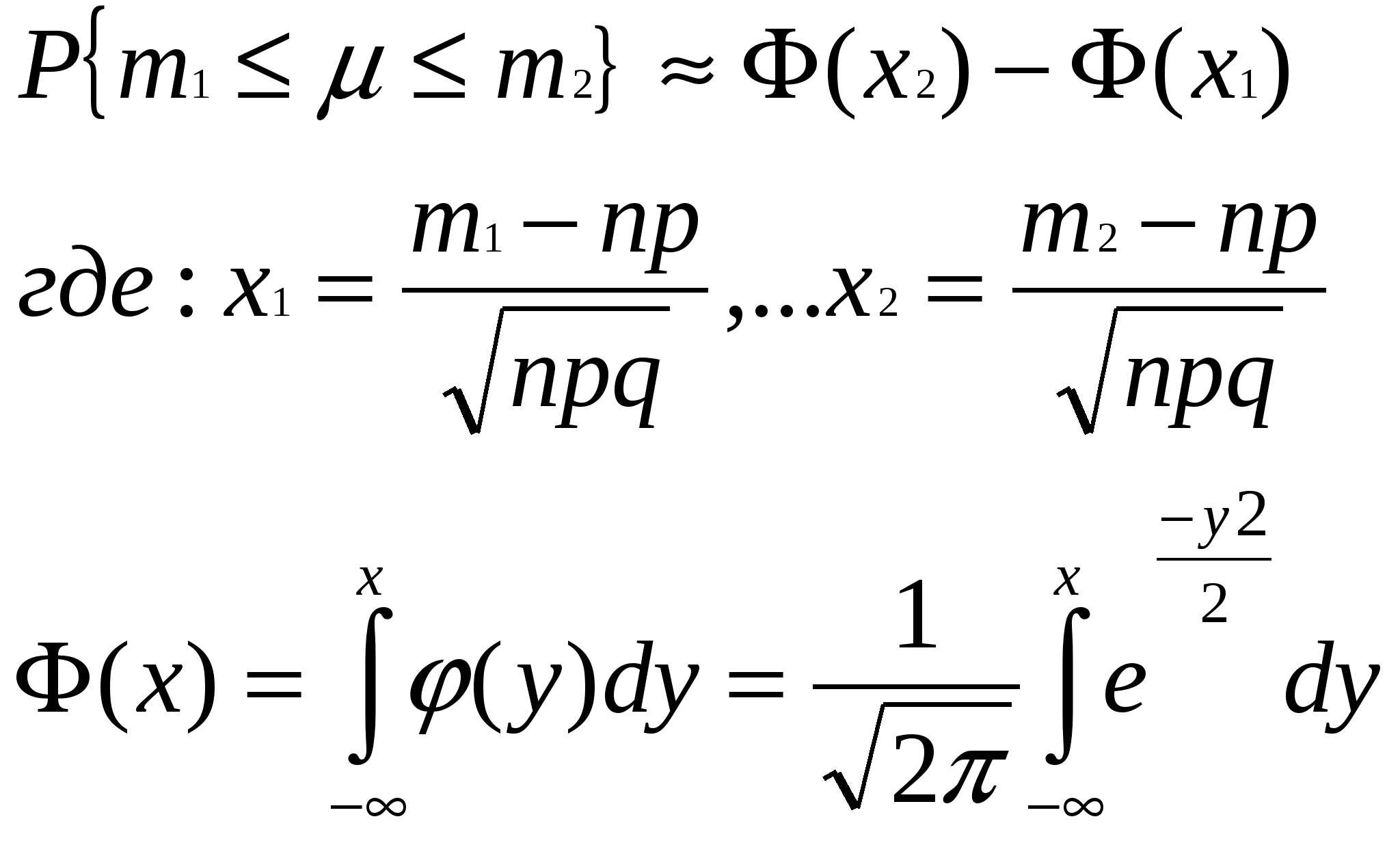 Функция Ф(х), фигурирующая в интегральной формуле Муавра-Лапласа, носит название функции стандартного нормального распределения. Она обладает свойством Ф(-х) = 1 – Ф(х). Иногда табулируют не Ф(х), а интеграл Лапласа В терминах интеграла Лапласа интегральная формула Муавра-Лапласа имеет вид: m1 = 790; m2 = 830; n = 900; p = 0,9; q = 0,1. 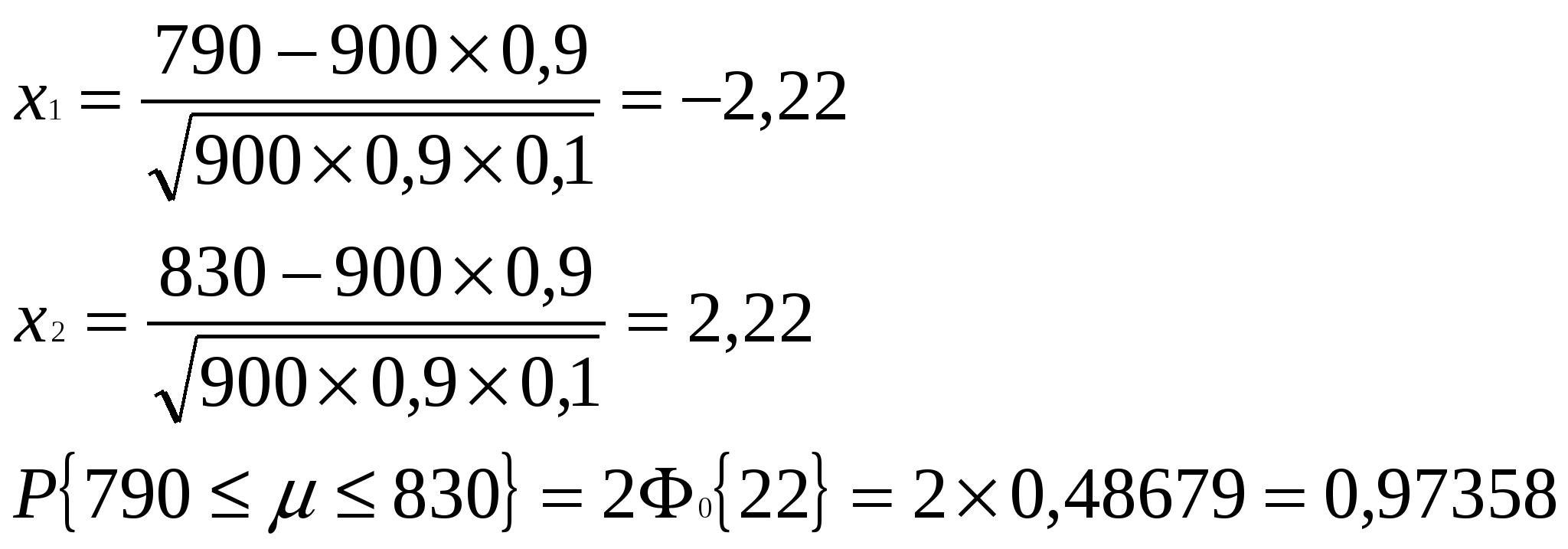 Ответ: а). 10-5 б). 0,97358. Задача №6. Условия: Инвестор покупает ценные бумаги за счет займа, взятого с процентной ставкой r под залог недвижимости. Процентная ставка на ценные бумаги X - случайная величина с МХ=а, a>r, DX=<72. Какова вероятность того, что инвестор не сможет вернуть долг и лишится своей недвижимости? Указание. Оценить с помощью неравенства Чебышева вероятность события (Х<г). Решения: Воспользуемся неравенством Бьенэме - Чербышева. Это неравенство является родоначальником многих других неравенств, широко применяемых в современной теории вероятностей. Это неравенство имеет смысл применять только тогда, когда ε>σ; в противном случае оно дает тривиальную оценку. Вероятность того, что отклонение случайной величины х от ее математического отклонения по абсолютной величине меньше положительного числа ε, не меньше чем 1- D(x) / ε2 В нашем случае ε = r; М(Х) = а; D(Х) = 0,72 Ответ: Задание №8. Условие: На крупном промышленном предприятии при проведении курса технической подготовки, предназначенного для всех принятых работников рабочих специальностей, было установлено, что имеется зависимость между возрастом работника и временем, необходимым для освоения определенных навыков и умений. В таблице приведен возраст 8 работников, выбранных произвольно, а также время, необходимого для выработки у них навыков в определенной области.
а) С помощью метода регрессии определите продолжительность подготовки, необходимую для нового работника в возрасте 30 лет. б) Определите коэффициент корреляции и прокомментируйте точность вашей оценки в том, что касается части (а). Какие другие факторы могут повлиять на продолжительность подготовки, необходимой для каждого работника? Решение: а). Из данных таблицы можно предположить наличие линейной зависимости между данными признаками. Построим расчетную таблицу, в которой факторным признаком будет число лет, а зависимым признаком – количество часов подготовки.
Запишем систему уравнений: 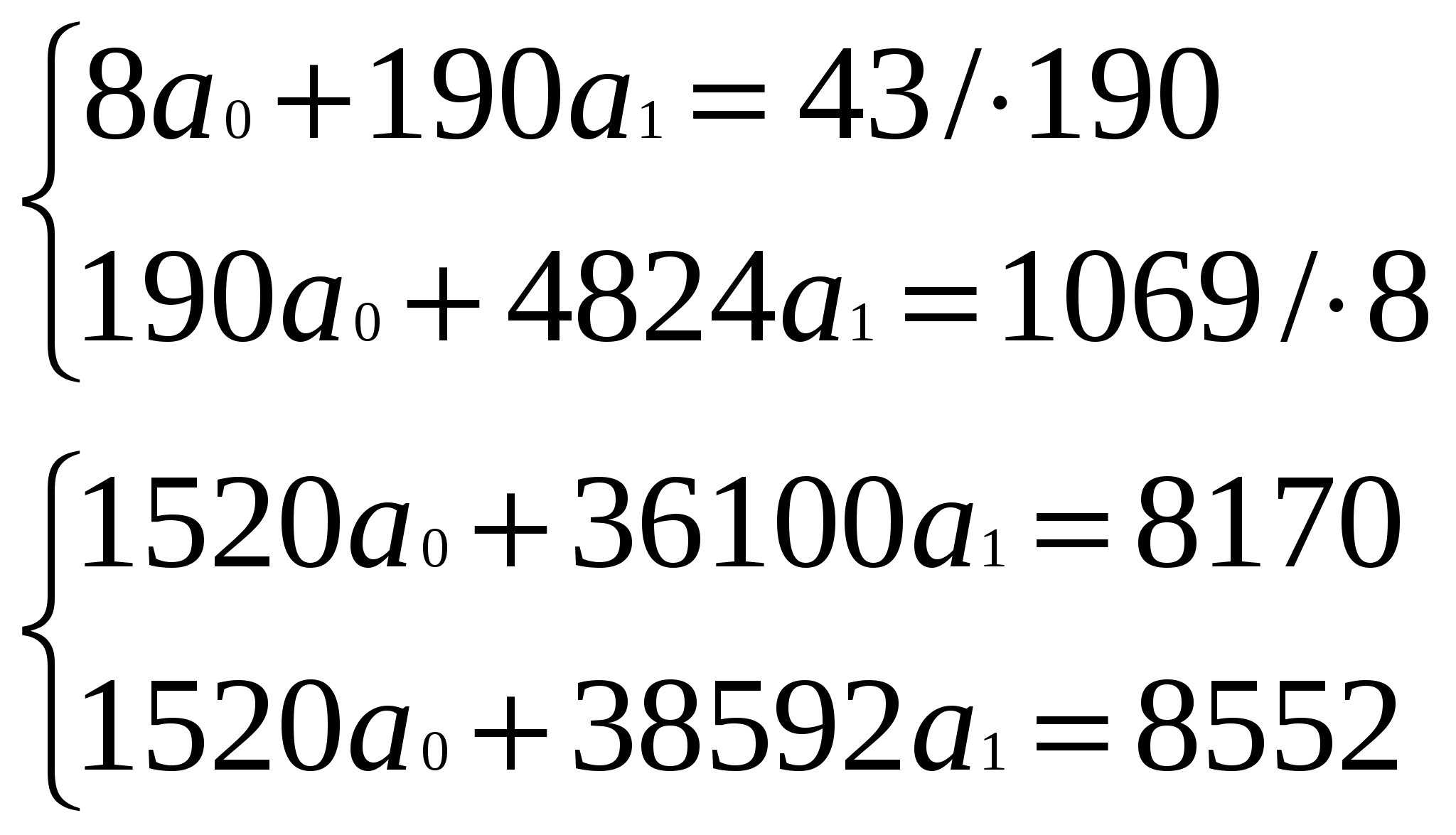 2492а1=382 а1 = 0,153 а0=(43 – 190 . 0,153) : 8 = 1,74 Следовательно: х=1,74 + 0,153 х При х = 30 = 1,74 + 0,153 . 30 = 6,33 С помощью метода регрессии получается, что для нового работника в возрасте 30 лет продолжительность подготовки будет равна 6,33 ч. б). δу2 = 2 – ()2 = 31,375 – 28,89 = 2,485 δх2 = 2 – ()2 603 – 564,063 = 39 Коэффициент корреляции равен 0,6. Можно сделать вывод о наличии существенной корреляционной связи. Ответ: а). при х = 30 у = 6,33. б). r = 0,6. Задание №9. Условие: Поступление страховых взносов в 130 филиалов страховых организаций в регионе А составило 26∙104 у.е., в регионе В на 100 филиалов пришлось 18∙104 у.е. Дисперсия величины страховых взносов в регионе А равна 39∙108 (у.е.)2 , в регионе В – 25∙108 (у.е.)2 . На уровне значимости а = 0,05 определите, существенно ли различается средняя величина поступления страховых взносов в регионах А и В из расчета на 1 филиал. Решение: Воспользуемся следующим правилом. Для того чтобы при заданном уровне значимости а проверить нулевую гипотезу Н0 : М(х) = М(у) о равенстве математических ожиданий (генеральных средних) двух нормальных генеральных совокупностей с известными дисперсиями (в случае больших выборок) при конкурирующей гипотезе Н1 : М(х) ≠ М(у), надо вычислить наблюдаемое значение критерия 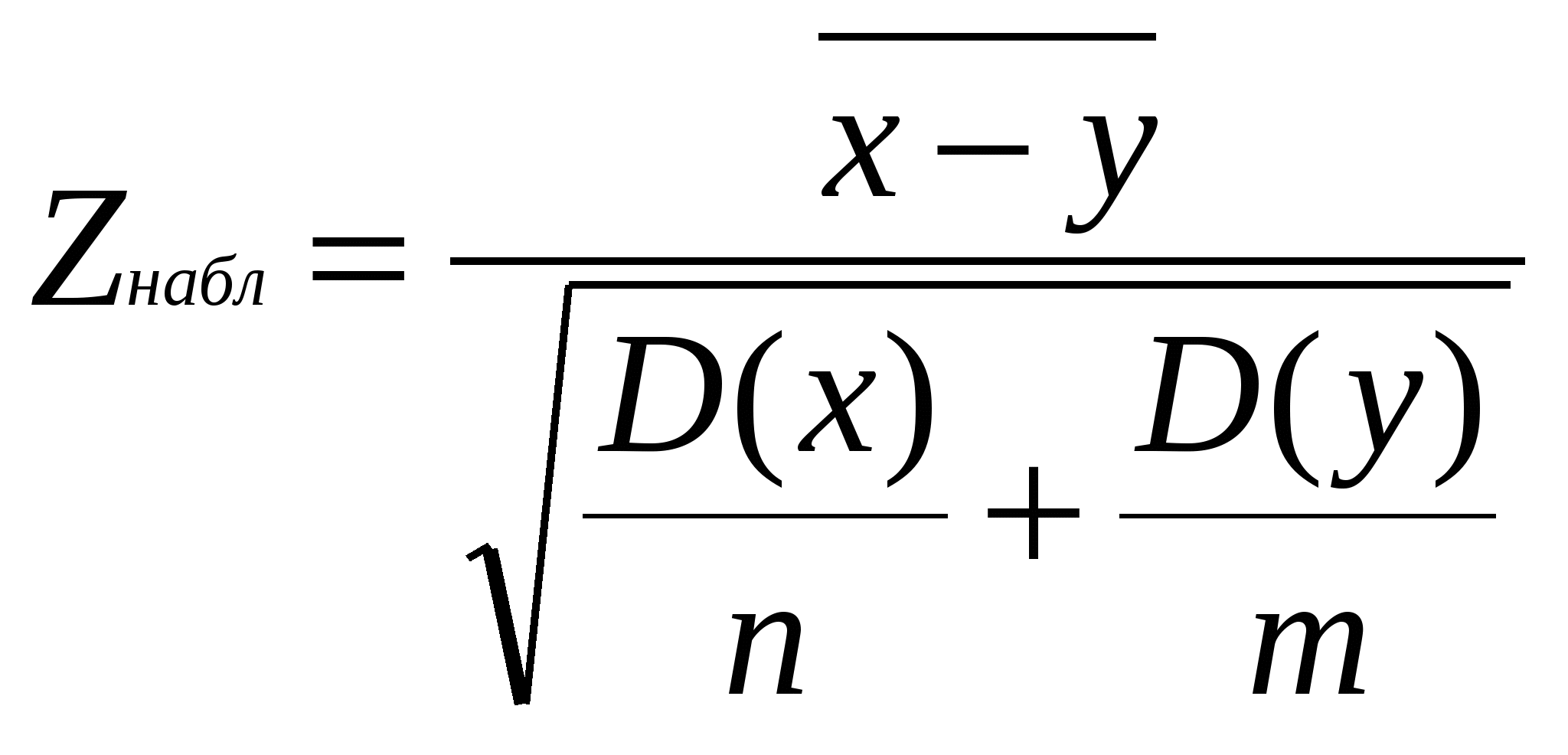 И по таблице функции Лапласа найти критическую точку Zкр из равенства Ф(Zкр) = (1 – 2 ) / 2 Если |Zнабл| < Zкр – нет оснований отвергать нулевую гипотезу. Если Zнабл > Zкр – нулевую гипотезу отвергают. Таким образом: 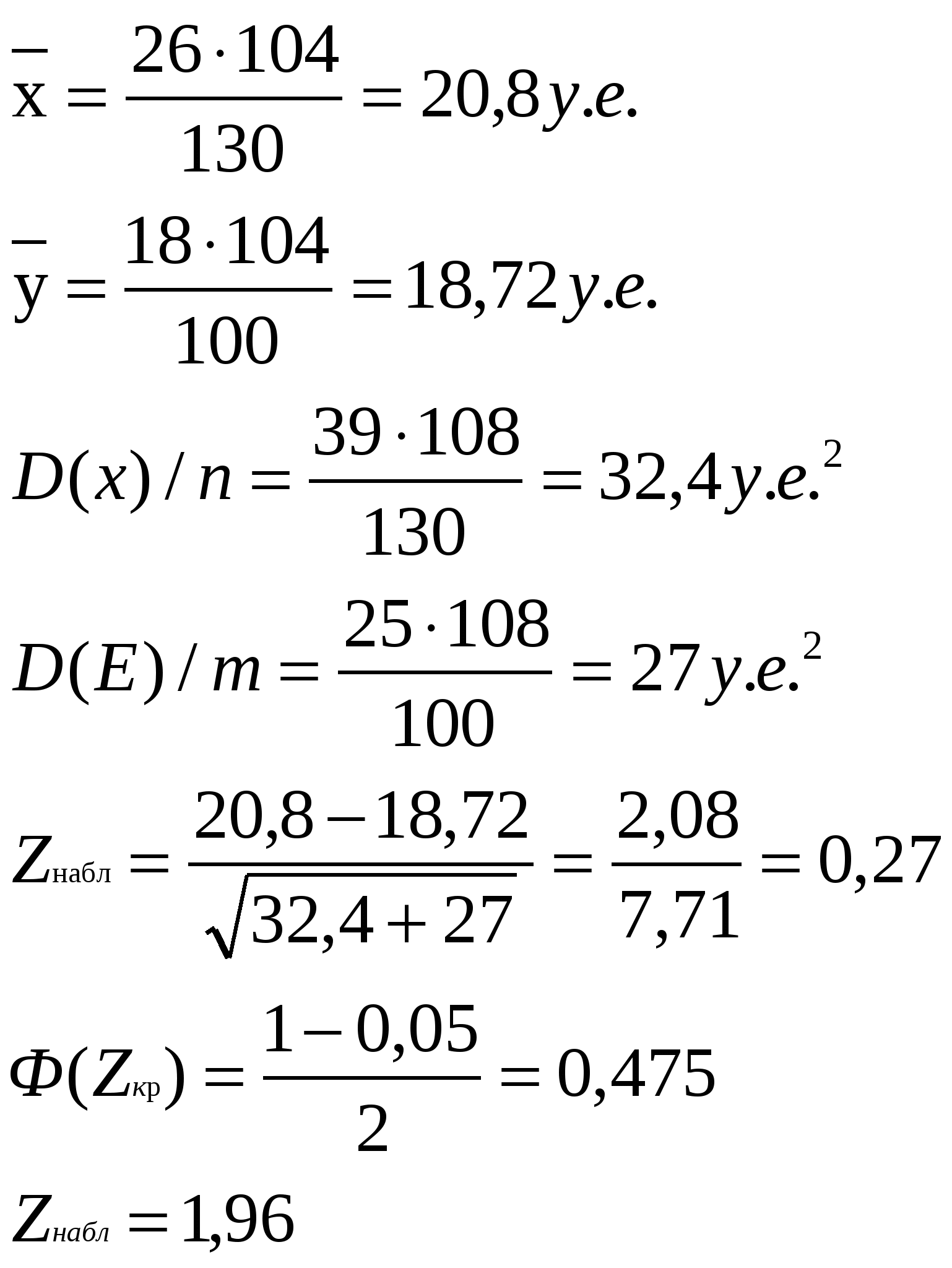 Ответ: Можно сделать вывод о равенстве средних величин на уровне значимости, а = 0,05. Задание №10. Условие: Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей (Х) и стоимостью ежемесячного технического обслуживания (Y). Для выяснения характера этой связи было отобрано 15 автомобилей. а). Постройте график исходных данных и определите по нему характер зависимости. б). Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при а = 0,05. в). Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
Решение: а). Построим график исходных данных: У 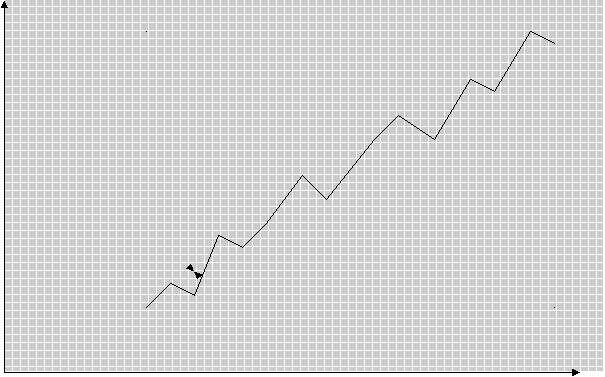 40 30 20 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20  По графику можем наблюдать наличие линейной корреляционной связи между данными критериями. б). Рассчитаем выборочный коэффициент линейной корреляции Пирсона, проверим его значимость при а = 0,05. Построим таблицу: = 377,4; = 26,27; = 13.
Тогда: 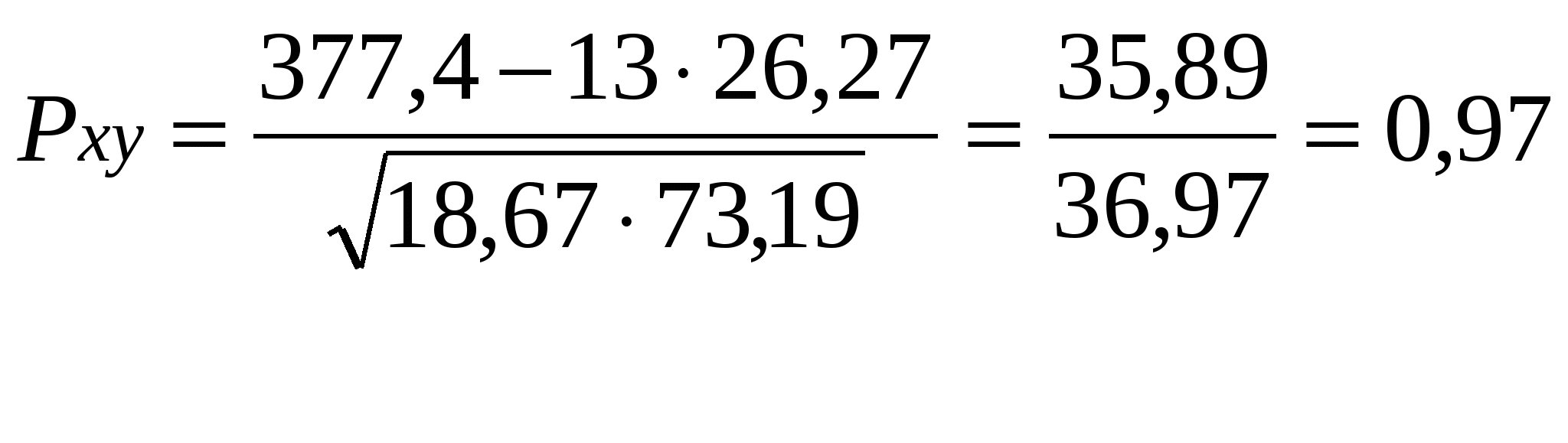 R = 15-2 = 13 – это число степеней свободы. а = 0,05 – уровень значимости по таблице найдем значение критической точки tкр (13; 0,05) = 2,16 Тнабл > tкр значит величина значимо коррелированна. в). Построим уравнение регрессии, решив следующую систему: 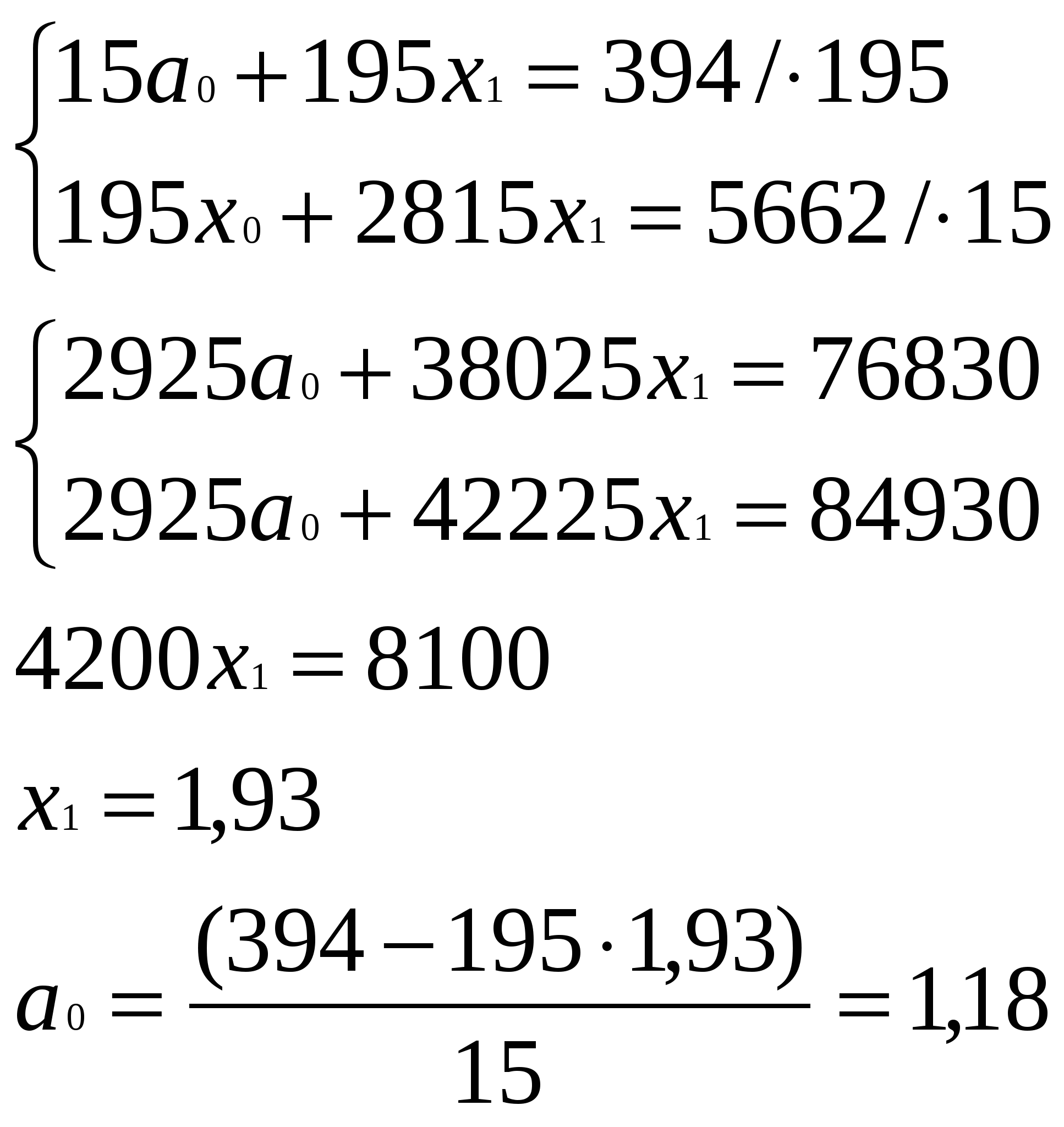 Таким образом у = 1,18 + 1,93х - искомое уравнение. Можно сделать вывод о наличии существенной прямой связи между пробегом автомобиля и стоимостью технического обслуживания. Ответ: а). По графику видно наличие линейной корреляционной связи между данными критериями. б). Тнабл = 3,61. Тнабл > tкр - это значит величина значимо коррелированна. в). Существует прямая связь между пробегом автомобиля и стоимостью технического обслуживания. Список использованной литературы:
|
