Контрольные работы. Контрольные работы по алгебре и началам математического анализа. Контрольные работы по алгебре и началам математического анализа 10 класс

• Название: Контрольные работы по алгебре и началам математического анализа 10 класс
• Анкор: Контрольные работы
• Дата: 12.04.2022
• Размер: 85.75 Kb.
• Имя файла: Контрольные работы по алгебре и началам математического анализа .docx
• Тип: Документы; #467371

Контрольные работы по алгебре и началам математического анализа 10 класс.

КР-1. Повторение и расширение сведений о функции.

1. 
   Найдите наибольшее и наименьшее значения функции:
   1) у = 7х – 2 на промежутке [–2; 3];
   2) у = х² – 2х – 3 на промежутке [–1; 2].
   
2. 
   Исследуйте на чётность функцию:
   1) у = x⁴ – 2х² + 3; 2) у = х⁵ – 3х³ + 2; 3) у = 2x/(5 – x⁶);   4) у = (x + 2)/(x² + 2x).
   
3. 
   Найдите функцию, обратную к функции у = 9 – 3х.
   
4. 
   Постройте график функции у = √[4 + 2х].
   
5. 
   Являются ли равносильными уравнения:
   1) х² = 49 и х² + 1/(x + 8) = 1/(x + 8) + 49;
   2) х² = 49 и х² + 1/(x+7) = 1/(x+7) + 49 ?
   
6. 
   На рисунке 31 изображена часть графика чётной функции у = f(x), определённой на промежутке [–6; 6]. Достройте график этой функции и найдите её наибольшее и наименьшее значения на промежутке [–6; 6].
   
7. 
   Решите неравенство: 1) (х + 1)(х – 11)(х + 9) > 0; 2) (5 – х)(х – 8)(х – 6)² ≤ 0;  
   

3) x/(x+3) + 5/x – 9/(x²+3x) ≥ 0.
КР-2. Степенная функция. Корень n-й степени и его свойства.

1. 
   При каких значениях а график функции у = ах^–3 + 2 проходит через точку А (–2; ¹/₈) ?
   
2. 
   Найдите значение выражения: 1) ³√[2 ¹⁰/₂₇] • ⁴√[5 ¹/₁₆] + 4 • ⁷√–128; 2) 3√[(3⁹ • 7³)/2¹²];   3) ⁴√[6 – 2√5] • 8;   4) ⁴√[6 – 2√5] • ⁴√[6 + 2√5].
   
3. 
   Решите уравнение: 1) 64х³ + 27 = 0; 4) ³√[х – 1] = –5;
   2) (х – З)⁵ = 32;   5) ⁴√[х + 1] = –3;
   3) (2х + 7)⁴ = 81;   6) ⁵√[x⁴ + 16] = 2.
   
4. 
   Найдите наибольшее и наименьшее значения функции у = х^–3 – 3 на промежутке [–3; –2].
   
5. 
   Упростите выражение: 1) ²⁰√a⁵; 2) 4√[a³ • 5√a];   3) ¹⁶√a¹⁶, если а ≥ 0;   4) ⁸√[(a + 9)⁸], если а ≤ –9.
   
6. 
   Определите графически количество решений системы уравнений
   { y = x^–2,
   [ y = x/3.
   
7. 
   Решите неравенство: 1) 3√[2x – 1] < –4; 2) 6√[13x – 1] < 2.
   
8. 
   Упростите выражение (⁸√a/(⁴√a – 16) + ⁸√a/(⁴√a – 8 • ⁸√a + 16)) • (4 – ⁸√a)²/(2 • ⁸√a) – ⁸√a/(⁸√a + 4).
   

КР-3. Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства.

• 
  1. Найдите значение выражения: 1) 0,25 • 64^1/3; 2) 36^1,5; 3) (1 ²⁴/₂₅)^–0,5.
  
• 
  2. Упростите выражение:  1) а^0,9 – а^2,4;   2) a^17/18 : а^1/12;   3) (а³)^–0,4 • (а^–5)^–0,2 : (а^–0,7)⁶;   4) (a^11/7b^3/14)^28/11.
  
• 
  3. Решите уравнение √[6х + 16] = х.
  
• 
  4. Сократите дробь:  1) (a – 9a^5/6)/(a^1/6 – 9);   2) (a^1/3 – 9b^1/6)/(a^1/6 + 3b^1/12); 3) …
  
• 
  5. Постройте график функции у = ((х + 5)^1/5)⁵.
  
• 
  6. Решите уравнение:  1) ³√[х + 7] – ⁶√[x + 7] =2;   2) √[x + 6] – √[x – 2] = 2.
  
• 
  7. Решите неравенство √[5x – 6] > x.
  

КР-4. Тригонометрические функции и их свойства.

1. Найдите значение выражения 4 sin (π/3) cos (–π/6) – ctg (–π/4) + √3 tg (π/3).

2. Определите знак выражения:  1) sin 181 cos (–302°) tg260°;   2) cos (–5π/9) tg (7π/5).

3. Исследуйте на чётность функцию:  1) f(x) = х⁴ + 4 sin² x cos 2x;   2) f(x) = (tg x – ctg x)/cos x.

4. Найдите значение выражения:  1) cos (25π/3);   2) ctg (–780°).

5. Сравните значения выражений:  1) sin (16π/15) и sin (17π/16);   2) ctg (–4π/7) и ctg (–5π/9).

6. Постройте график функции f(x) = cos (x – π/6), укажите промежутки её возрастания и убывания.

7. Постройте график функции у = √[sin2x – 1] – 1.

КР-5. Соотношение между тригонометрическими функциями одного и того же аргумента. Формулы сложения и их следствия.

1. Упростите выражение:  1) (cos²6a – 1)/(1 – sin²6a) – tg 12a ctg 12a;
2) sin 8a cos 3a – cos 8a sin 3a;
3) (4 cos²7а)/(sin 14а);
4) (sin 14а – sin 10а)/(cos 3a – cos 7a);
5) cos²(π/2 – За) – cos²(π + 3a);
6) 2 cos 8a cos 9a – cos 17a.

2. Дано: tg a = 5, tg b = 1,5, 0 < a < π/2, 0 < b < π/2. Найдите a + b.

3. Докажите тождество:  1) ctg 2b – ctg 4b = 1/(sin 4b);   2) …

4. Найдите наибольшее и наименьшее значения выражения 4 sin 2a ctg a – 1.

 КР-6. Тригонометрические уравнения и неравенства.

1. Решите уравнение:  1) sin (8x – π/3) = 0;   2) cos (x/6 + π/4) = √2/2;   3) tg² 4x + tg 4x = 0.

2. Решите неравенство:  1) cos (x/7) ≤ 1/2;   2) ctg (7x + 2π/3) > –√3/3

3. Решите уравнение:  1) 4cos² x + 4sin x – 1 = 0;   2) 3sin² 3x – 2,5sin 6x + 1 = 0;   3) sin 9х + sin 8x + sin 7x = 0.

4. Вычислите:  1) sin (arcsin ⁵/₈);   2) cos (arcsin ⁵/₁₃).

5. Решите уравнение sin 6x + √3 cos 6x = –2 cos 8x.

КР-7. Производная. Уравнение касательной.

1. Найдите производную функции:  1) f(х) = 2х⁵ – x³/3 + 3х² – 4;   2) f(x) = (3х – 5) √x;   3) f(x) = (x² + 9x)/(х – 4);   4) f(x) = 2/x³ – 3/x⁶.

2. Найдите уравнение касательной к графику функции f(x) = х⁴ – 2х в точке с абсциссой х₀ = –1.

3. Найдите производную данной функции и вычислите её значение в данной точке х₀:  1) f(x) = √[3х + 1], х₀ = 5;   2) f(х) = sin⁵ х, х₀ = π/3.

4. Материальная точка движется по координатной прямой по закону s(t) = –t³/3 + 2,5t² + 24t + 7 (время t измеряется в секундах, перемещение s – в метрах). Найдите скорость движения точки в момент времени t₀ = 3.

5. Найдите уравнение касательной к графику функции f(x) = х² + 3х – 8, если эта касательная параллельна прямой у = 9х – 1.

КР-8. Применение производной.

1. Докажите, что функция f(х) = –х³/3 + х²/2 – 2х + 12 убывает на множестве действительных чисел.

2. Найдите промежутки возрастания и убывания и точки экстремума функции:  1) f(x) = х³ – х² – 5х – 3;   2) f(х) = х√[9 – х];   3) f(x) = √3х – 2 cos x.

3. Найдите наибольшее и наименьшее значения функции f(x) = (x² + 7x)/(х – 9) на промежутке [–4; 1].

4. Исследуйте функцию f(x) = х³ – 3х² и постройте её график.

КР-9. Обобщение и систематизация знаний учащихся.

1. Сравните ³√2[√3] и ⁶√5[√6].

2. Найдите область определения функции f(x) = √[(9 – x²)/(x² – 6x + 8)].

3. Решите уравнение:  1) √[2x – 1] = х – 2;   2) 8 sin (x/3) + cos (x/3) = 0;   3) cos 6x – 5 cos 3x + 4 = 0.

4. Докажите тождество (sin 8а / sin 5a – cos 8a / cos 5a) • ((sin 6а + sin 14а) / sin За) = 4 cos 4а.

5. Решите неравенство √[1 – 5х] < х + 1.

6. Исследуйте функцию f(x) = х³ – 6х² и постройте её график.

Контрольные работы по геометрии 10 класс.

КР-1. Аксиомы стереометрии и следствия из них. Начальные представления о многогранниках.

1. 
   На рисунке 97 изображён куб ABCDA₁B₁C₁D₁. Укажите прямую пересечения плоскостей АВ₁С₁ и ABB₁.
   
2. 
   Даны точки А, В и С такие, что АВ = 2 см, ВС = 5 см, АС = 3 см. Сколько существует плоскостей, содержащих точки А, В и С? Ответ обоснуйте.
   
3. 
   Точки А, В и С не лежат на одной прямой. На прямой АВ отметили точку D, на прямой ВС — точку В, а на прямой DE — точку М. Докажите, что точки А, С и М лежат в одной плоскости.
   
4. 
   Точки М и N принадлежат соответственно граням SBC и SCD пирамиды SABCD (рис. 98). Постройте точку пересечения прямой MN с плоскостью SBD.
   
5. 
   Точки М и К принадлежат соответственно рёбрам SB и SC тетраэдра SABC, а точка N — грани АВС (рис. 99), причём прямые МК и ВС не параллельны. Постройте сечение тетраэдра плоскостью MNK.
   

КР-2. Параллельность в пространстве.

1. Даны параллельные плоскости α и β. Через точки А и В плоскости проведены параллельные прямые, пересекающие плоскость β в точках А₁ и В₁. Найдите А₁В₁, если АВ=5см.
2. Верно, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости.
3. Две плоскости параллельны между собой. Из точки М, не лежащей ни в одной из плоскостей, ни между плоскостями, проведены две прямые, пересекающие эти плоскости соответственно в точках А₁ и А₂, В₁ и В₂. Известно, что МА₁=4см, В₁В₂=9см, А₁А₂=МВ₁. Найдите МА₂ и МВ₂.
4. Построить сечение,

проходящее через линии и точки,

выделенные на чертеже (рис. 1).
5. Ребро куба АВСДА₁В₁С₁Д₁ равно 2см. Найдите расстояние между прямыми АВ и В₁Д.

КР-3. Перпендикулярность прямой и плоскости.

1. 
   На рисунке 103 изображён ромб ABCD. Через точку О пересечения его диагоналей проведена прямая МО, перпендикулярная прямой АС. Докажите, что прямая АС перпендикулярна плоскости BMD.
   
2. 
   Через вершину А прямоугольного равнобедренного треугольника АВС с гипотенузой АВ, равной 8 см, проведена прямая AD, перпендикулярная плоскости треугольника. Расстояние от точки D до плоскости АВС равно 2 см. Найдите расстояние от точки D до прямой ВС.
   
3. 
   Точка F равноудалена от всех вершин прямоугольника со сторонами 12 см и 16 см и находится на расстоянии 2√11 см от плоскости прямоугольника. Найдите расстояние от точки F до вершин прямоугольника.
   
4. 
   Через вершину В квадрата ABCD к его плоскости проведён перпендикуляр МВ. Точка М удалена от стороны AD на 9√2 см. Найдите расстояние от точки М до плоскости квадрата, если его диагональ равна 14 см.
   
5. 
   Точка S равноудалена от сторон трапеции ABCD (ВС || AD) и находится на расстоянии √7 см от её плоскости. Найдите расстояние от точки D до сторон трапеции, если CD = 12 см, ∠ADC = 45°.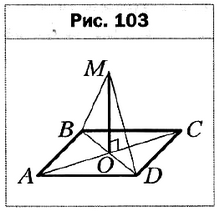
   

КР-4. Угол между прямой и плоскостью. Угол между плоскостями. Перпендикулярные плоскости.

1. 
   Из точки А проведены к плоскости α наклонные АЕ и AF, образующие с ней углы 30° и 60° соответственно. Найдите проекцию наклонной AF на плоскость α, если проекция наклонной АЕ на эту плоскость равна 6 см.
   
2. 
   Точка В принадлежит одной из граней двугранного угла и удалена от другой грани на 4√3 см. Найдите расстояние от точки В до ребра двугранного угла, если величина этого угла равна 60°.
   
3. 
   Угол между плоскостями треугольников АВМ и АВК равен 30°, AM = ВМ = 20 см, АК = ВК = 2√67 см, АВ = 32 см. Найдите отрезок МК.
   
4. 
   Плоскости α и β перпендикулярны. Прямая а — линия их пересечения. В плоскости α выбрали точку А, а в плоскости β — точку В такие, что расстояния от них до прямой а равны 4 см и 5 см соответственно. Найдите расстояние между точками А и В, если расстояние между их проекциями на прямую а равно 2√2 см.
   
5. 
   Через вершину В квадрата ABCD провели перпендикуляр МВ к плоскости квадрата. Угол между прямой MD и плоскостью квадрата равен 60°. Найдите угол между плоскостями АВС и MCD.
   

КР-5. Многогранники.

1. 
   Основанием прямой призмы является прямоугольный треугольник, катеты которого равны 6 см и 8 см. Найдите площадь полной поверхности призмы, если её боковое ребро равно 5 см.
   
2. 
   Сторона основания правильной треугольной пирамиды равна 4√3 см, а высота пирамиды — 2√6 см. Найдите: 1) боковое ребро пирамиды; 2) площадь боковой поверхности пирамиды.
   
3. 
   Найдите площадь боковой поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 6 см и 22 см, а боковое ребро — 4√5 см.
   
4. 
   Основанием пирамиды является равнобедренный треугольник с боковой стороной а и углом α при вершине. Двугранные углы пирамиды при рёбрах основания равны β. Найдите: 1) площадь боковой поверхности пирамиды; 2) высоту пирамиды.
   
5. 
   В наклонной треугольной призме, боковое ребро которой равно 18 см, проведено сечение, перпендикулярное боковому ребру. Это сечение является треугольником со сторонами 3 см и 8 см и углом 60° между ними. Найдите площадь боковой поверхности призмы.
   

КР-6. Обобщение и систематизация знаний учащихся.

1. 
   Сторона правильного треугольника равна 6√3 см. Точка М равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость треугольника является точка, принадлежащая этому треугольнику. Найдите расстояние от точки М до сторон треугольника, если расстояние от точки М до плоскости треугольника равно 6√2 см.
   
2. 
   Точка А находится на расстоянии 3 см от плоскости α. Наклонные АЕ и AF образуют с плоскостью α углы 60° и 30° соответственно. Найдите расстояние между точками Е и F, если угол между проекциями наклонных на плоскость α равен 120°.
   
3. 
   Через вершину В треугольника АВС, в котором АВ = ВС = 6 см, АС = 8 см, проведён перпендикуляр МВ к плоскости треугольника. Найдите угол между плоскостями АВС и АМС, если МВ = 2√15 см.
   
4. 
   Основанием прямого параллелепипеда является ромб с острым углом α. Большая диагональ параллелепипеда равна d и образует с плоскостью основания угол β. Найдите площадь боковой поверхности параллелепипеда.
   
5. 
   Боковые грани DAB и DAC пирамиды DABC перпендикулярны плоскости основания. Найдите площадь боковой поверхности пирамиды, если ∠ACB = 90°, АС = 8 см, ВС = 6 см, а расстояние от точки D до прямой ВС равно 17 см.