Оалазвз. К.Р.МАТЕМАТ.1 курс ТПОП, ТЭТ. Контрольные работы по математике для студентов 1 курса заочного отделения специальностей тпоп и тэт полной и сокращенной форм обучения Правила выполнения и оформления контрольных работ

• Название: Контрольные работы по математике для студентов 1 курса заочного отделения специальностей тпоп и тэт полной и сокращенной форм обучения Правила выполнения и оформления контрольных работ
• Анкор: Оалазвз
• Дата: 01.12.2022
• Размер: 0.92 Mb.
• Имя файла: К.Р.МАТЕМАТ.1 курс ТПОП, ТЭТ.doc
• Тип: Контрольная работа; #823921
• страница: 4 из 5

5. Найти неопределенные интегралы
1.	а) ;	б) ;	в) .
2.	а) ;	б) ;	в) .
3.	а) ;	б) ;	в) .
4.	а) ;	б) ;	в) .
5.	а) ;	б) ;	в) .
6.	а) ;	б) ;	в) .
7.	а) ;	б) ;	в) .
8.	а) ;	б) ;	в) .
9.	а) ;	б) ;	в) .
10.	а) ;	б) ;	в) .
11.	а) ;	б) ;	в) .
12.	а) ;	б) ;	в) .
13.	а) ;	б) ;	в) .
14.	а) ;	б) ;	в) .
15.	а) ;	б) ;	в) .
16.	а) ;	б) ;	в) .
17.	а) ;	б) ;	в) .
18.	а) ;	б) ;	в) .
19.	а) ;	б) ;	в) .
20.	а) ;	б) ;	в) .

6.	Воспользовавшись соответствующим приложением предельного интеграла к задачам геометрии, найти следующее:
а) площадь фигуры, ограниченную линиями:
1. y = x2 , y = ;			2. y2 = 2x + 1, x – y – 1= 0;
3. y = x2 , y = ;			4. y2 = 9x , y = x + 2;
5. , y = 1, y = 4;			6. y = e , x = 0 , x = 2 ;
7. y = x , x = e-1, x = e;			8. y = x2, y = x3 ;
9. y = 2x , x = 0 , x = 2;			10. y = 9 - x2, y = 0.
б) Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями.
11. ,			12. , , , ;
13. , ,			14. , ;
15. ,			16. , , ;
17. , , ;			18. , , ;
19. , , ,			20. , .

Ранг матрицы

В этом разделе рассмотрим еще одну важную числовую характиристику матрицы, связанную с тем, насколько ее строки (столбцы) зависят друг от друга.

Определение 14.10 Пусть дана матрица размеров и число , не превосходящее наименьшего из чисел и : . Выберем произвольно строк матрицы и столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных строк и столбцов, называется минором порядка матрицы .

Пример 14.9 Пусть .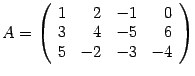

Минором первого порядка является любой элемент матрицы. Так 2, , -- миноры первого порядка.

Миноры второго порядка:

1. 
   возьмем строки 1, 2, столбцы 1, 2, получим минор ;
   
2. 
   возьмем строки 1, 3, столбцы 2, 4, получим минор ;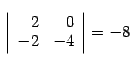
   
3. 
   возьмем строки 2, 3, столбцы 1, 4, получим минор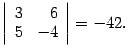
   

Миноры третьего порядка:

строки здесь можно выбрать только одним способом,

1. 
   возьмем столбцы 1, 3, 4, получим минор ;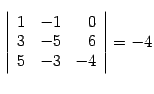
   
2. 
   возьмем столбцы 1, 2, 3, получим минор .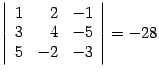
   

Предложение 14.23 Если все миноры матрицы порядка равны нулю, то все миноры порядка , если такие существуют, тоже равны нулю.

Доказательство. Возьмем произвольный минор порядка . Это определитель матрицы порядка . Разложим его по первой строке. Тогда в каждом слагаемом разложения один из множителей будет являться минором порядка исходной матрицы. По условию миноры порядка равны нулю. Поэтому и минор порядка будет равен нулю.