определения линал
1, 2


|
3
Тригонометрическая форма комплексного числа
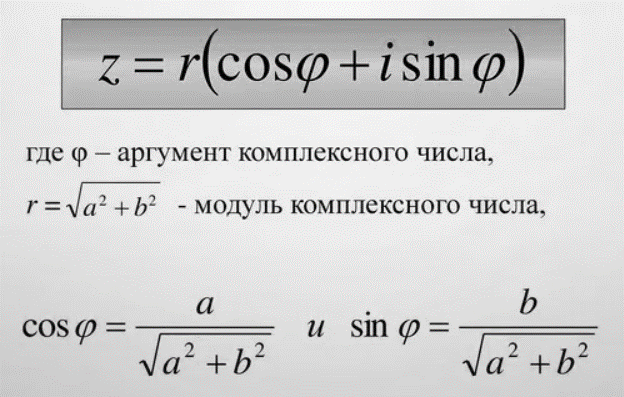
|
4
Показательная форма записи комплексного числа
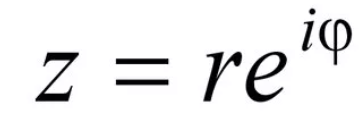
где r – модуль комплексного числа
|
5

|
6

|
7

|
8

*из лекции: Пусть дан определитель ∆ порядка n. Выберем целое число k, удовлетворяющее условию 1 ≤ k ≤ n−1, и в определителе ∆ выберем произвольные k строк и k столбцов. Элементы, стоящие на пересечении выбранных строк и столбцов, очевидно составляют квадратную матрицу порядка k. Определитель этой матрицы называется минором k-го порядка определителя ∆
|
9

|
10

|
11
Любой числовой набор α1, α2, . . . , αn называется решением системы линейных уравнений, если после подстановки этих чисел в систему вместо соответствующих неизвестных все уравнения системы обращаются в верные числовые равенства (тождества): b1 = b1, b2 = b2, . . . , bm = bm
|
12
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение
|
13
Система линейных уравнений называется несовместной, если она не имеет решений
|
14
Система называется неопределенной, если ее решений больше чем одно
|
15
Система называется определенной, если она обладает только одним решением
|
16
Однородные системы - системы, в которых все свободные члены равны нулю. Отличие однородных систем линейных уравнений от остальных состоит, по-крайней мере, в том, что любая однородная система всегда совместна, так как имеет нулевое решение.
|
17

|
18

|
19
Опр1. Система векторов a1, a2, . . . , ak пространства An называется линейно зависимой, если хотя бы один из этих векторов является линейной комбинацией остальных (линейно выражается через остальные).
Опр2. Система векторов a1, a2, . . . , ak пространства An называется линейно зависимой, если существует такой набор чисел γ1, γ2, . . . , γk, среди которых не все равны нулю, и при этом выполняется равенство γ1a1 + γ2a2 + · · · + γkak = o.
|
20
Опр1. Система векторов a1, a2, . . . , ak пространства An называется линейно независимой, если ни один из этих векторов не является линейной комбинацией остальных (не выражается линейно через остальные)
Опр2. Система векторов a1, a2, . . . , ak пространства An называется линейно независимой, если равенство γ1a1 + γ2a2 + · · · + γkak = o может выполняться только тогда, когда все коэффициенты в правой части одновременно равны нулю γ1 = 0, γ2 = 0,. . . ,γk = 0.
|
21
Базисом на плоскости называются два неколлинеарных вектора, параллельных этой плоскости, взятые в определенном порядке
|
22
Базисом в пространстве называются три некомпланарных вектора, взятые в определенном порядке
|
23
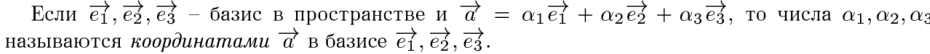
|
24

|
25
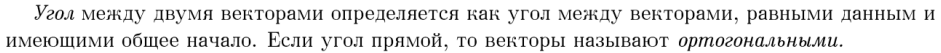
|
26
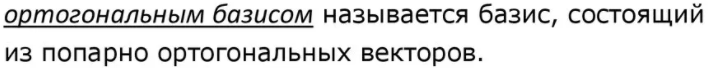
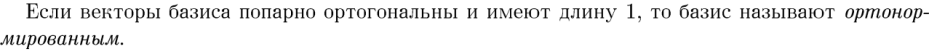
|
27

|
28

|
29
Два вектора называются коллинеарными, если существует прямая, которой они параллельны

|
30
Три вектора называются компланарными, если существует плоскость, которой они параллельны

|
31

|
32

|
33
Всякую максимальную линейно независимую систему векторов пространства An будем называть базисом этого пространства.
|
34
Рангом системы векторов пространства An называется число векторов, входящих в любую ее максимальную линейно независимую подсистему, т. е. в любой базис данной системы
|
35
Рангом матрицы A называется наивысший порядок отличных от нуля ее миноров
|
36
Горизонтальный ранг матрицы – это максимальное число ее линейно независимых строк или число ее базисных строк. Вертикальный ранг матрицы – это максимальное число ее линейно независимых столбцов или число ее базисных столбцов.
|
37

|
38
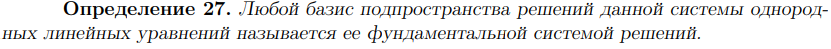
|
39

|
40

|
41

|
42
Вид квадратичной формы называется каноническим, если все ее ненулевые слагаемые содержат только квадраты неизвестных
|
43
критерий: Только невырожденные матрицы могут иметь обратные, а также обратная матрица для данной также является невырожденной.
|
44
Теорема Крамера: Если основная матрица квадратной системы линейных уравнений невырожденная, то такая система имеет единственное решение
|
45
Следствие из теоремы Крамера: Если квадратная однородная система линейных уравнений имеет ненулевые решения, то определитель ее основной матрицы необходимо равен нулю
|
46

|
47
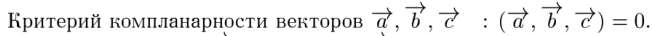
|
48

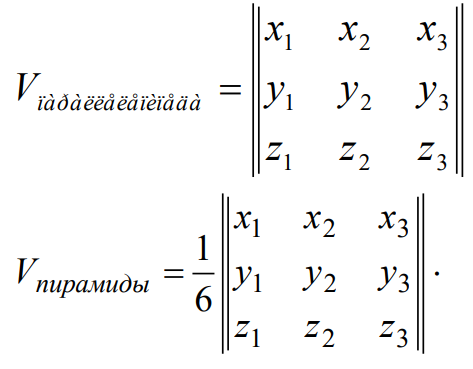
|
49

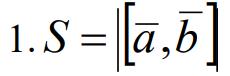 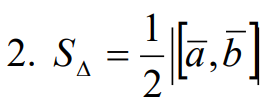
|
50
Теорема Кронекера – Капелли: Система линейных уравнений тогда и только тогда совместна, когда ранг расширенной матрицы A¯ равен рангу ее основной матрицы A
|
51
Теорема: Если в однородной системе линейных уравнений число уравнений меньше числа ее неизвестных, то такая система кроме нулевого будет иметь бесчисленное множество ненулевых решений.
Утверждение: Применяя метод Гаусса к любой однородной системе линейных уравнений, можно получить лишь следующие окончательные возможности:
1. Система преобразовалась к «треугольному» виду. Тогда исходная система имеет только нулевое решение;
2. Система преобразовалась к «трапецеидальному» виду. В этом случае исходная система имеет кроме нулевого еще бесчисленное множество ненулевых решений.
|
52
свойства векторного произведения двух векторов

|
53
Формула вычисления векторного произведения через координаты векторов в правом ортонормированном базисе.
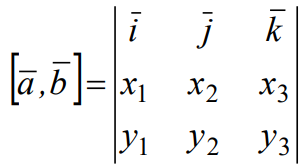
|
55
свойства смешанного произведения трех векторов

|
56
Формула вычисления смешанного произведения через координаты векторов в правом ортонормированном базисе.

|
58
Формула Муавра

|
|
 Скачать 2.76 Mb.
Скачать 2.76 Mb.