|
|
Физика. Контрольная 27. Контрольные вопросы к лабораторной работе 27
Контрольные вопросы к лабораторной работе №27
1. Линии индукции магнитного поля — воображаемые линии в пространстве, касательные к которым в каждой точке совпадают с направлением индукции магнитного поля.
Линии индукции магнитного поля непрерывны (не имеют ни начала, ни конца), замыкаются сами на себя. Это характерно для любых магнитных полей. Поля, обладающие таким свойство, называют вихревыми.

2. Теорема гласит: Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.
Если соленоид бесконечно длинный, то индукция магнитного поля на оси соленоида определяется по формуле:
B = μ0⋅μ⋅I⋅n,
где μ0=4π∙10-7 Гн/м – магнитная постоянная;
μ - магнитная проницаемость среды, внутри соленоида;
I - сила тока в соленоиде;
n – плотность намотки соленоида (число витков на единицу длины).
Так как в условии задачи не сказано, какая среда внутри соленоида, то будем считать, что он находится в вакууме (μ=1).
n = 2N/l
где N – число витков, 2N, т.к. катушка двухслойная; l – длина соленоида.
Так как витки плотно прилегают друг к другу, то Связь между N и l имеет вид:
l = N * d
где d – диаметр провода.

3. Закон Био-Савара Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке.
Получаем закон Био-Савара-Лапласа: Элемент тока 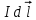 создает на расстоянии r магнитное поле с индукцией создает на расстоянии r магнитное поле с индукцией  * * 
Этот закон позволяет, зная токи, рассчитать магнитное поле в любой точке пространства. Чтобы найти поле, созданное всем проводником с током, надо проинтегрировать полученное для  выражение по всей длине проводника: выражение по всей длине проводника:

Вычислим индукцию на оси кругового витка радиуса R с током I. на оси кругового витка радиуса R с током I.
Каждый элемент тока 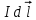 создает в точке А на оси витка на расстоянии „х“ от его центра О поле создает в точке А на оси витка на расстоянии „х“ от его центра О поле  . Для определения результирующей индукции . Для определения результирующей индукции  направленной в силу симметрии вдоль оси витка, надо суммировать проекции всех векторов направленной в силу симметрии вдоль оси витка, надо суммировать проекции всех векторов  на ось: на ось:

Так как r2 = R2 + x2 и cosβ = cos( - a) = sin a = - a) = sin a = 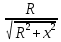 то индукция то индукция  направленная вдоль оси х, уменьшается с расстоянием х от центра витка О и имеет величину направленная вдоль оси х, уменьшается с расстоянием х от центра витка О и имеет величину 
В центре же кругового витка с током 
4. Значение магнитной индукции на оси катушки рассчитывается по формуле
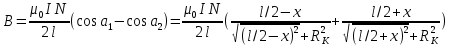
где I – ток, протекающий по катушке, N – число витков катушки, l – длина катушки, м., а1 и а2 — углы между направлением оси х и радиус — векторами, проведенными из точки на оси к краям катушки, рад; х — координата точки на оси катушки, в которой определяется величина магнитной индукции, м.; RK – радиус катушки.
5. Для расчета величины магнитной индукции на оси соленоида в центре ВЦ и торце ВТ получим:
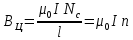

где NC – число витков соленоида, n = NC/l – число витков на единицу соленоида.
6. Гальванометр — прибор, в котором используется явление взаимодействия катушки с током и магнита. Гальванометр показывает наличие тока и его направление.
Заряд, протекающий по контуру при кратковременном импульсе тока, можно измерить с помощью баллистического гальванометра, который представляет собой гальванометр с большим периодом собственных колебаний.
Практически каждый гальванометр имеет один и тот же принцип работы:
- При прохождении электрического тока по катушке, вокруг нее создается магнитное поле. Оно взаимодействует с магнитным полем, которое создает постоянный магнит.
- В результате, образуется сила, вызывающая поворот или вращение катушки.
- Преодолев сопротивление пружины, она стремится занять свое место между полюсами постоянного магнита.
- Одновременно с перемещением катушки, происходит и перемещение указателя.
- Расстояние, на которое они переместили, составляет пропорцию с количеством тока, протекающим через катушку.
7. В 1831 г. Фарадей открыл, что во всяком замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление называют электромагнитной индукцией, а возникающий ток индукционным.
Сам по себе электрический ток возникнуть не может, следовательно, в описанной ситуации в контуре возникает электродвижущая сила (Э.Д.С.) индукции. В результате многочисленных опытов М. Фарадей установил, что Э.Д.С. индукции пропорциональна скорости изменения магнитного потока, пронизывающего поверхность, натянутую на контур. Выбором подходящей системы единиц можно обеспечить не только пропорциональность, но и строгое равенство упомянутых величин:
 , , 
где S – поверхность, натянутая на контур. Примечательно, что изменение величины Ф за счет изменения во времени индукции магнитного поля  или за счет изменения взаимной ориентации векторов или за счет изменения взаимной ориентации векторов  и нормали и нормали  или за счет изменения площади поверхности S приводит к одинаковым результатам. или за счет изменения площади поверхности S приводит к одинаковым результатам.
Размер измерительной катушки должен быть малым по следующим причинам:
- Магнитное поле убывает пропорционально кубу расстояния от источника, поэтому для катушек больших размеров оно может иметь существенную неоднородность в пределах зоны потокосцепления.
- Для калибровки большой катушки потребуются кольца Гельмгольца или калибровочный соленоид с зоной однородности соответствующих размеров.
- Катушки малых размеров дешевле и проще в изготовлении.
8. При пропускании тока через обмотку соленоида возникает магнитное поле, укорачивающее ферромагнитный стержень — отрицательная стрикция. В результате укорачивания стержня каток, на который стержень опирается, перемещается, прикрепленное к катку зеркальце поворачивается, что фиксируется на экране как перемещение „светового зайчика“.
При выключении тока световой зайчик возвращается в исходное положение.
Значение вращающего момента пропорционально измеряемой электрической величине. Для того чтобы обеспечить однозначную связь между углом поворота подвижной части и значением измеряемой величины, необходимо в каждом аналоговом приборе создавать противодействующий момент, пропорциональный углу поворота подвижной части механизма.
Вращающий момент прямо пропорционален величине тока I, площади контура S и синусу угла между направлением магнитного поля и нормали
M IS sin(n, B)
где М — вращающий момент или момент силы
IS = Pm – магнитный момент контура
9. При включении и выключении тока I1 световой зайчик гальванометра отклоняется в противоположные стороны на шкале. Это связано с тем, что при включении тока I1 индукционный ток Ii в измерительной цепи имеет одно направление, в при выключении тока — другое направление. Согласно правилу Ленца индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока через контур, в котором течет этот ток. При выключении тока I1 индукционный ток будет противодействовать нарастанию потокосцепления ψ2 в контуре 2, вследствие чего поток нарастает постепенно. При выключении тока I1 индукционный ток будет препятствовать уменьшению этого потока.
10. Величина смещения светового указателя (зайчика) по шкале гальванометра является мерой величины заряда, протекающего через гальванометр.
Так как цепь гальванометра замкнута, то в ней возникает ток

Следовательно, величина заряда протекающего во вторичной обмотке при переключении пропорциональна индукции магнитного поля в сердечнике.
С другой стороны, заряд ∆ q пропорционален отклонению зайчика по шкале гальванометра

CБ — баллистическая постоянная гальванометра, равная величине заряда вызывающего отклонения зайчика на одно деление, n – число делений на которое произошло отклонение. Из вышеприведенных формул получаем расчетную формулу для индукции
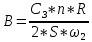 или или
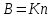 , ,

11. Считается что баллистический гальванометр вносит меньше искажений в измерение по сравнению с амперметром потому что отличается более высокой чувствительностью к току и сравнительно большим периодом колебаний подвижной системы. |
|
|
 Скачать 5.77 Mb.
Скачать 5.77 Mb.