Рол. Контрольные вопросы. Контрольные вопросы Переменный ток электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным

• Название: Контрольные вопросы Переменный ток электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным
• Дата: 08.12.2022
• Размер: 267.15 Kb.
• Имя файла: Контрольные вопросы.docx
• Тип: Контрольные вопросы; #834661

Контрольные вопросы

1. 
   Переменный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
   
2. 
   В электрических цепях переменного тока ток, падение напряжения и ЭДС являются синусоидальными функциями времени –
   

Среднее значение синусоидального тока: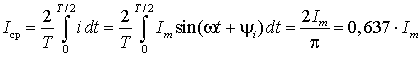



Для напряжений и ЭДС средние значения:



Временная диаграмма:

3. 
   На комплексной плоскости:
   

Соотношение отображений синусоидальных функций во временной и векторной формах.

4. 
   Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в:
   

• 
  Показателной
  
• 
  Тригонометрической
  
• 
  Алгебраической -формах
  

ЭДС: ( )



Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:



Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами.



Мгновенное значение напряжени

5. 
   Действующего значения синусоидального тока запишем: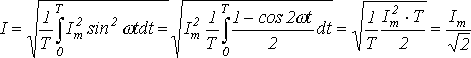
   

Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз

6. 
   Амплитудные значения синусоидального тока напряжения и мощности совпадают со значениями постоянного тока.
   
7. 
   Преимущества синусоидального тока по сравнению с любым другим видом переменного тока обусловлены относительно простым способом его получения, а также более высоким коэффициентом полезного действия генераторов, двигателей, трансформаторов и линий электропередач.
   
8. 
   Закон Ома в векторной форме.
   
   
9. 
   Законы (правила) Кирхгофа в векторной форме.
   1-закон Кирхгофа
   
   Геометрическая сумма векторов всех токов, подходящих к любому узлу цепи, равна нулю.
   2-ой закон Кирхгофа
   
   Геометрическая сумма векторов всех ЭДС любого контура цепи равна сумме векторов напряжений на всех участках этого контура.
   
10. 
    Математическая модель, описывающая свойства резистивного сопротивления, определяется законом Ома:
    

,
Коэффициенты пропорциональности и называются соответственно сопротивлением и проводимостью элемента и являются его количественной характеристикой. Зависимость (3.1) называется вольт-амперной характеристикой (ВАХ) резисторного сопротивления. Если , то ВАХ – линейна б), если , то ВАХ – нелинейна
Зависимость тока от приложенного напряжения в индуктивном элементе определяется зависимостью: ,
где – константа интегрирования, численно равная начальному току,
Разница между синусоидальный ток и постоянного тока в том , что имеются разные зависимости тока . тем самым в синусоидальном токе могут меняться значения

11. 
    Фазовый сдвиг можно измерить непосредственно по осциллограммам исследуемых напряжений, наблюдая их одновременно на экране осциллографа.
    Очевидно, что , где a – расстояние в делениях между пересечениями осциллограммами нулевой линии; b – длительность периода, выраженная в делениях шкалы. Для этих измерений используют осциллограф с двухлучевой электронной трубкой или со встроенным электронным коммутатором. Погрешность измерения угла j этим способом определяется погрешностями измерения длин отрезков а и b:
    

,
где – погрешность измерения j; – абсолютные погрешности измерения отрезков а и b.
Можно считать максимально возможной погрешностью одно малое деление шкалы осциллографа ; .

12. 
    Амплитудное - это верхняя точка синусоиды напряжения
    

Действующее - это 0.7 от амплитудного

Мгновенное - в какой то момент времени напряжения

13. 
    Расчет и векторная диаграмма ЭЦ с активным сопротивлением.
    

Мгновенное значение тока в цепи определяется по закону Ома

,
где

Мгновенная мощность такой цепи равна произведению мгновенных значений тока и напряжения.

Построим волновую и векторную диаграммы цепи переменного тока с активным сопротивлением.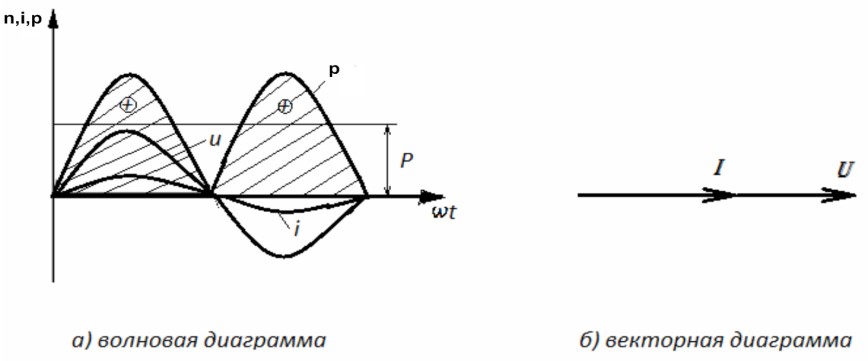

Волновая и векторная диаграммы цепи переменного тока с активным сопротивлением.
Как видно из волновой диаграммы, потребление мощности в сети с активной нагрузкой периодически изменяется от нуля до максимального значения и опять до нуля. При этом знак мощности всё время остаётся положительным. Это означает, что в активной нагрузке происходит процесс необратимого преобразования электрической энергии в тепловую энергию.
Мощность цепи переменного тока принято оценивать по среднему значению мгновенной мощности за период: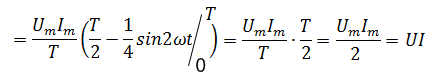
=
Следовательно, в цепи переменного тока с активным сопротивлением активная мощность определяется как произведение действующих значений тока и напряжения:

14. 
    Многие элементы электрических установок состоят из индуктивных катушек, обладающих индуктивностью L. При включении такой катушки в цепь переменного тока, в ней мгновенно проявляется действие ЭДС самоиндукции - 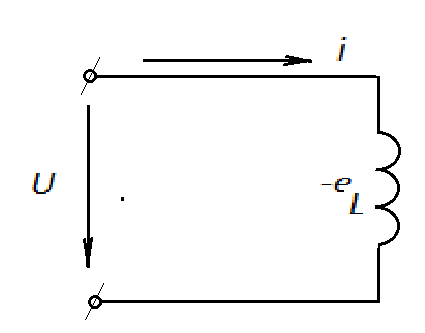, препятствующее изменению тока. Величина этой ЭДС настолько значительна, что на ее уравновешивание затрачивается основная часть напряжения, приложенного к катушке, и лишь его небольшая часть приходится на падение напряжения в активном сопротивлении катушки. Поэтому часто активное сопротивление катушки приравнивается к нулю, и такую катушку называют идеальной катушкой индуктивности. Цепь переменного тока с такой катушкой называется цепью с индуктивной нагрузкой.
    
    Цепь переменного тока с индуктивной нагрузкой.
    К зажимам цепи подведено синусоидальное напряжение u. Под действием этого напряжения в цепи возникает ток, мгновенное значение которого равно
    (2.8.)
    Ток возбуждает в катушке ЭДС самоиндукции, пропорциональную скорости изменения тока в цепи
    (2.9)
    В любой момент времени ЭДС самоиндукции - уравновешивается напряжением на зажимах цепи u
    (2.10)
    Подставляя (2.8) и (2.10) в (2.9), имеем:
    (2.11)
    где амплитудное значение напряжения:
    (2.12)
    Разделив обе части уравнения (2.12) на , получим выражение закона Ома для цепи с идеальной катушкой индуктивности.
    (2.13)
    Рассмотрим размерность знаменателя выражения (2.13)
    Обозначим и назовем индуктивным сопротивлением идеальной катушки. Его величина зависит от индуктивности катушки и частоты питающего тока.
    Сравнивая между собой уравнения (2.8) и (2.11) делаем вывод: в цепи переменного тока с индуктивной нагрузкой напряжение опережает ток на угол в 90°.
    Мгновенная мощность цепи определяется как произведение мгновенных значений тока и напряжения, т.е.
    
    Построим векторную и волновую диаграммы цепи с индуктивным сопротивлением
    Рис. 2.7 Векторная и волновая диаграммы цепи переменного тока с индуктивным сопротивлением.
    Анализ волновой диаграммы позволяет сделать следующие выводы:
    В течение первой и третьей четвертей периода переменного тока при его изменении от нуля до амплитудного значения, мощность положительна. Это означает, что энергия, посылаемая источником во внешнюю цепь, запасается в катушке индуктивности в форме энергии магнитного поля
    ..
    Мощность цепи с идеальной катушкой оценивают по величине индуктивной мощности Q_L, измеряемой в ВАр (вольт-ампер реактивный) и характеризующей интенсивность обмена энергией между генератором и магнитным полем катушки .
    Индуктивная мощность в отличие от активной мощности не может быть использована в практических целях.
    
15. 
    Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение (см. рис. 4), то ток iчерез него будет равен:
    

.

(3)

Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы uи i, то на его экране будет иметь место картинка, соответствующая рис. 5.

Из (3) вытекает:

;

 

.

 
Введенный параметр называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при конденсатор представляет разрыв для тока, а при .

Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

;

,

- разделим первый из них на второй:



или

.

(4)

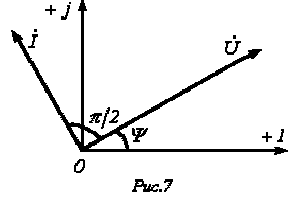В последнем соотношении - комплексное сопротивление конденсатора. Умножение на соответствует повороту вектора на угол по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.

16. 
    Рассмотрим цепь, состоящую из реальной катушки, имеющей активное сопротивление R и индуктивное сопротивление X_L, и конденсатора с емкостным сопротивлением Х_с, включенных последовательно (рис. 2.11).
    

Для удобства анализа работы цепи воспользуемся векторной диаграммой цепи. При построении векторной диаграммы (рис. 2.12) произведем векторное сложение напряжений на всех элементах цепи:



Это выражение представляет собой запись второго закона Кирхгофа в векторной форме.

Построение векторной диаграммы начинаем с вектора величины, общей для всех элементов цепи. При последовательном соединении таким базисным вектором является вектор тока I.

Вектор напряжения на активном сопротивлении U_a = R1 совпадает по направлению с вектором тока, его называют активной составляющей напряжения.

Вектор напряжения на индуктивном сопротивлении U_L = X_LI опережает вектор тока / на угол я/2 (направлен вверх). Вектор напряжения на емкостном сопротивлении U_c = Х_С1 отстает от вектора тока / на угол я/2 (направлен вниз). Замыкающий вектор изображает приложенное к цепи напряжение U, сдвинутое по фазе относительно тока на угол (р.



Рис. 2.11. Последовательное включение активного, индуктивного и емкостного сопротивлений



Рис. 2.12. Векторная диаграмма напряжений



Рис. 2.13. Треугольник напряжений



Рис. 2.14. Треугольник сопротивлений

При построении диаграммы условно принято, что U_L > U_c.

Выделим из векторной диаграммы треугольник ОАВ (рис. 2.13). Этот треугольник называется треугольником напряжений.

Вектор АВ называется реактивной составляющей напряжения:



Из треугольника напряжений получается простое соотношение



Если все стороны треугольника напряжений ОАВ разделить на величину тока, получим треугольник сопротивлений (рис. 2.14).

Гипотенуза этого треугольника соответствует полному сопротивлению Z.

Разность индуктивного и емкостного сопротивлений называется реактивным сопротивлением: X = X_L - Х_с

Из треугольника сопротивлений получаются важные расчетные соотношения: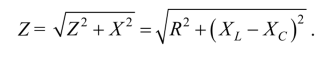

Закон Ома для цепи имеет вид / = U/Z

17. 
    Основной составляющей считается активная мощность. Она представляет собой величину, характеризующую процесс преобразования электрической энергии в другие виды энергии. То есть по-другому является скоростью, с какой потребляется электроэнергия. Именно это значение отображается на электросчетчике и оплачивается потребителями. Вычисление активной мощности выполняется по формуле: P = U x I x cosф.
    
    
    

В отличие от активной, которая относится к той энергии, которая непосредственно потребляется электроприборами и преобразуется в другие виды энергии – тепловую, световую, механическую и т.д., реактивная мощность является своеобразным невидимым помощником. С ее участием создаются электромагнитные поля, потребляемые электродвигателями. Прежде всего она определяет характер нагрузки, и может не только генерироваться, но и потребляться. Расчеты реактивной мощности производятся по формуле: Q = U x I x sinф .Полной мощностью является величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителям необходимое количество электроэнергии и поддерживает их в рабочем состоянии. S= sqrt(Q^2 + P^2)

18. 
    Активная мощность, потребляемая двухполюсником, не может быть отрицательной (иначе двухполюсник не потреблял бы энергию, а генерировал бы еѐ), поэтому cos ф ≥ 0
    
19. 
    При величине sin φ для значений φ от 0 до плюс 90° является положительной величиной. При sin φ для значений φ от 0 до −90° является отрицательной величиной.