корни. Корень натуральной степени из числа. Корень натуральной степени из числа
 Скачать 32.68 Kb. Скачать 32.68 Kb.
|
|
Корень натуральной степени из числа. 1. Вычислите: 22=4 (2*2=4) 33=27 (3*3*3=27) 62=36 (6*6=36) 72=49 (7*7=49) 2. Изучение новой темы ОПРЕДЕЛЕНИЕ. Корнем n-ной степени из числа a называется такое число, n-ная степень которого равна a. ОПРЕДЕЛЕНИЕ. Арифметическим корнем n-ной степени из числа а называют неотрицательное число, n-ная степень которого равна a. 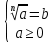 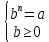 (n-я степень b равна подкоренному выражению a) (n-я степень b равна подкоренному выражению a)Основное тождество 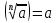 Число n называется показателем корня, а само число а - подкоренным выражением. Корень n-й степени из числа 0 =0 ; корней четной степени из отрицательных чисел не cyществует. Для корней нечетной степени справедливо равенство 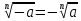 Пример 1:  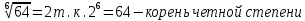 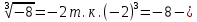 не арифметический корень, а не арифметический корень, а 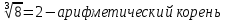 Основные свойства арифметических корней n-ной степени: Для любого натурального n, целого k и любых Неотрицательных чисел a и b выполнены равенства: 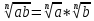 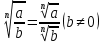 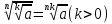 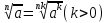 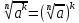 Пример 2: Найдите значение: а) 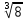 ; б) ; б) 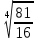 а) 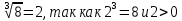 б) 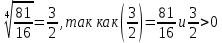 Пример 3. Решить уравнение: 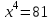 Уравнение 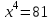 имеет два действительных корня: это числа 3 и – 3 т.к. имеет два действительных корня: это числа 3 и – 3 т.к. 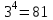 и и 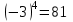 . Таким образом: . Таким образом: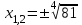 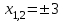 Пример 4. Решить уравнение: х5= 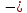 11 11По определению корня n – й степени число х – корень пятой степени из – 11. Показатель корня – нечетной степени число 5, поэтому такой корень существует, и притом только один: это 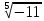 . Итак, . Итак, 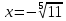 Пример 5. Вычислить: а) 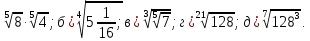 а) 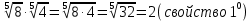 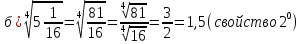 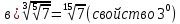 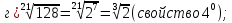 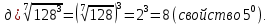 Пример 6. Сравнить числа 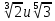 Представим 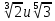 в виде корней с одним и тем же показателем: в виде корней с одним и тем же показателем: 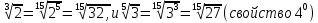 . Из неравенства . Из неравенства 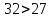 по по 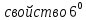 следует, что следует, что 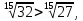 и, значит, и, значит, 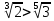 . .3. Вычислить и проверить себя по эталону: а) 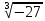 б) 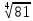 в) 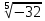 г) 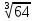 Эталон: а) 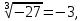 б) 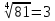 в) 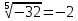 г) 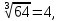 Решить уравнение и проверить себя по эталону а) 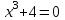 ; б) ; б) 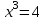 Эталон: а) х3+4=0 б) х3=4 х3=-4 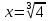 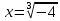 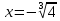 |
