Статистика Практическая работа. Ковалев Виктор Николаевич
 Скачать 109.35 Kb. Скачать 109.35 Kb.
|
Практическое задание
дисциплине
Пермь 2022 Содержание Задача 1 2 3адача 2 5 Задача 3 6 Задача 4 7 Задача 5 9 Задача 6 11 Список использованных источников 12 Задача 1Условие: Имеются следующие данные за год по заводам одной промышленной компании, таблица 1. Таблица 1 – Исходные данные
На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три. Решение: Определим выработку на одного рабочего по формуле: В=В/( Ч) где В – выпуск продукции, Ч – число рабочих. Представим расчет в виде таблицы 2. Таблица 2 - Выработка для каждого завода
Продолжение таблицы 2
Величина интервала: i=(Xmax-Xmin)/(n) , где Xmax и Xmin – максимальное и минимальное значения признака т.е. число рабочих, а n – число групп. i=(1900-700)/( 3)=400 - получили 3 группы: 1гр. - от 700 до 1100 рабочих 2 гр. – от 1100 до 1500 рабочих 3 гр. – от1500 до 1900 рабочих Составим таблицу 3. Таблица 3 - Рабочая таблица
Продолжение таблицы 3
По данным рабочей таблицы составляем аналитическую группировку, таблица 4. Таблица 4 – Аналитическая группировка
На основании таблицы 4, можно сделать следующий вывод, что с увеличением количества рабочих увеличиваются основные фонды и выработка на одного рабочего. 3адача 2Условие: Выпуск продукции на заводе в 2018 г. составил 160 млн руб. По плану на 2019 г. предусматривалось выпустить продукции на 168 млн руб., фактически же выпуск составил 171,36 млн руб. Вычислите относительные величины планового задания и выполнения плана. Решение: На основе имеющихся данных рассчитаем относительные показатели: - относительная величина планового задания:  - относительная величина выполнения плана:  Вывод: в 2019 году планировалось увеличить объем производства продукции на 5% по сравнению с 2018 г., по итогам года план производства продукции был перевыполнен на 2%. Задача 3Условие: На основании данных, представленных в таблице 1, определите установленную среднюю продолжительность трудового дня производственного рабочего по заводу в целом. Таблица 1 – Исходные данные
Решение. Найдем количество рабочих в каждом цеху: Цех 1 – 600*3=1800 Цех 2 – 800*3=2400 Цех 3 – 400*2=800 Цех 4 – 200*1=200 Найдем общее количество рабочих на заводе: Робщ= Цех 1+ Цех 2 + Цех 3 + Цех 4 Робщ= 1800 + 2400 + 800 + 200 = 5200 Определим количество рабочих работающих по 8 часов: 1800 + 2400 + 800 = 5000 Или 5000/5200*100%=96,15% Определим количество рабочих работающих по 6 часов: 200 Или 200/5200*100%=3,85% Тогда можно определить среднюю продолжительность смены: 8*96,15%+6*3,85% =8*0,9615+6*0,0385= 7,692+0,231=7,923 часа. Задача 4Условие: Имеются следующие данные о распределении рабочих цеха по размеру месячной заработной платы, таблица 1. Таблица 1 – Исходные данные
Определите среднюю месячную зарплату рабочих цеха, моду и медиану, среднеквадратическое отклонение и коэффициент вариации. Решение: Среднюю месячную зарплату определим по формуле:  , , где 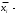 середина i-го интервала, середина i-го интервала,  число рабочих в i-м интервале число рабочих в i-м интервалеСоставим вспомогательную таблицу 2, для расчета показателей. Таблица 2 – Вспомогательная таблица
 Следовательно, средняя месячная зарплата рабочих цеха составляет 10,083 тыс. руб. Так как ряд имеет равные интервалы, то мода находится в интервале с наибольшей частотой, то есть в интервале 10,0 - 12,5 тыс. руб. Следовательно, её можно вычислить по формуле:  где 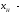 нижняя граница модального интервала нижняя граница модального интервала величина модального интервала величина модального интервала частота модального периода частота модального периода предмодального периода предмодального периода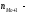 постмодального периода постмодального периода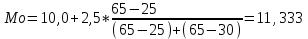 Следовательно, наиболее часто встречающаяся заработная плата 11, 333 тыс. руб. Определим медиану по формуле: 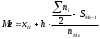 где 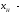 нижняя граница медианного периода нижняя граница медианного периода величина медианного периода величина медианного периода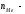 частость медианного периода частость медианного периода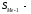 накопленная частость предмедианного периода накопленная частость предмедианного периода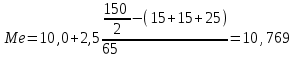 Дисперсию можно определить по формуле:  Среднеквадратическое отклонение: 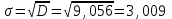 Коэффициент вариации  Поскольку V ≤ 33%, то совокупность однородна, а вариация слабая. Таким образом, можно сделать следующий вывод: каждое значение ряда отличается от среднего значения 10,083 в среднем на 3,009. Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки. Поскольку коэффициент вариации меньше 33%, то совокупность однородна. Полученным результатам можно доверять. Задача 5Условие: Объем продукции на промышленном предприятии повысился в 2013 году по сравнению с 2008 годом на 100 млн рублей в сопоставимых ценах, или на 25 %. В 2018 году объем продукции увеличился по сравнению с 2013 годом на 20 %. Определите: 1) объем выпуска продукции предприятия в 2008, 2013, 2018 годах; 2) среднегодовые темпы прироста выпуска продукции за: а) 2008-2013гг.; б) 2013-2018 гг.; в) 2008-2018 гг. Решение: Найдем объем выпуска продукции предприятия по годам: - 2008 год: ВП2008 = 100 / 0,25 = 400 млн.руб. - 2013 год: ВП2013 = 400 + 100 = 500 млн.руб. - 2018 год: ВП2018 = 500 * (1 + 0,2) = 600 млн.руб. Найдем среднегодовые темпы прироста выпуска продукции по формуле:  , ,где 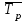 - среднегодовой темп роста. - среднегодовой темп роста.Среднегодовой темп роста найдем по формуле: 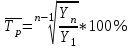 2008-2013: 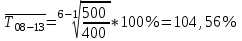 Тогда темп прироста 2008-2013 составит: 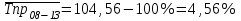 2013-2018 гг: 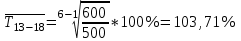 Тогда темп прироста 2013-2018 гг составит: 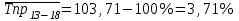 2008-2018гг  Тогда темп прироста 2008-2018 гг составит: 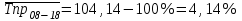 Вывод: В 2008 году выпуск продукции составил 400 млн. руб., в 2013 году – 500 млн. руб, а в 2013 году – 600 млн. руб. В 2008 - 2013 гг. объем выпуска продукции на промышленном предприятии ежегодно увеличивался в среднем на 4,56 %, в период с 2013 г. по 2018 г. ежегодный темп прироста выпуска продукции составлял 3,71%, а в целом за период с 2008 г. по 2018 г. объем выпуска продукции на промышленном предприятии ежегодно увеличивался в среднем на 4,14%. Задача 6Условие: По одному из предприятий промышленности стройматериалов имеются следующие данные, таблица 1. Таблица 1 – Исходные данные
Определите общий индекс цен и сумму роста или снижения объема реализации продукции за счет изменения цен. Решение: Найдем индивидуальные индексы цен. Строительные блоки: iр= (100% – 2%)/100% = 0,98 Панели: iр = (100%+5%)/100% = 1,05 Строительные детали: ip=1 Тогда общий индекс цен найдем по формуле: 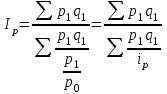 , ,где p – цены, q – физический объем, pq – объем реализации продукции, индексом 0 обозначены данные базисного периода, индексом 1 – данные отчетного периода. 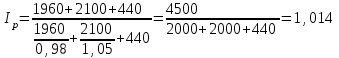 Определим сумму роста (снижения) объема реализации продукции за счет снижения цен: 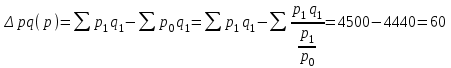 тыс. руб. тыс. руб.Таким образом, общий индекс цен составил 1,014, а объем реализации продукции за счет снижения цен увеличился на 60 тыс. руб. Список использованных источниковБалдин, К. В. Общая теория статистики : учеб. пособие / К. В. Балдин, А. В. Рукосуев. – 2-е изд. – М. : Дашков и К, 2017. – 312 с. Глинский, В. В. Статистика : учеб. / В. В. Глинский. – ИНФРА-М, 2017 – 355 с. Дудин, М. Н. Теория статистики : учеб. и практикум для академического бакалавриата / М. Н. Дудин, Н. В. Лясников, М. Л. Лезина. М. : Юрайт, 2018. 148 с. Ефимова, М. Р. Общая теория статистики. Практикум : учеб. пособие для академического бакалавриата / М. Р. Ефимова [и др.]; под ред. М. Р. Ефимовой. 4-е изд., перераб. и доп. М. : Юрайт, 2018. 355 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
