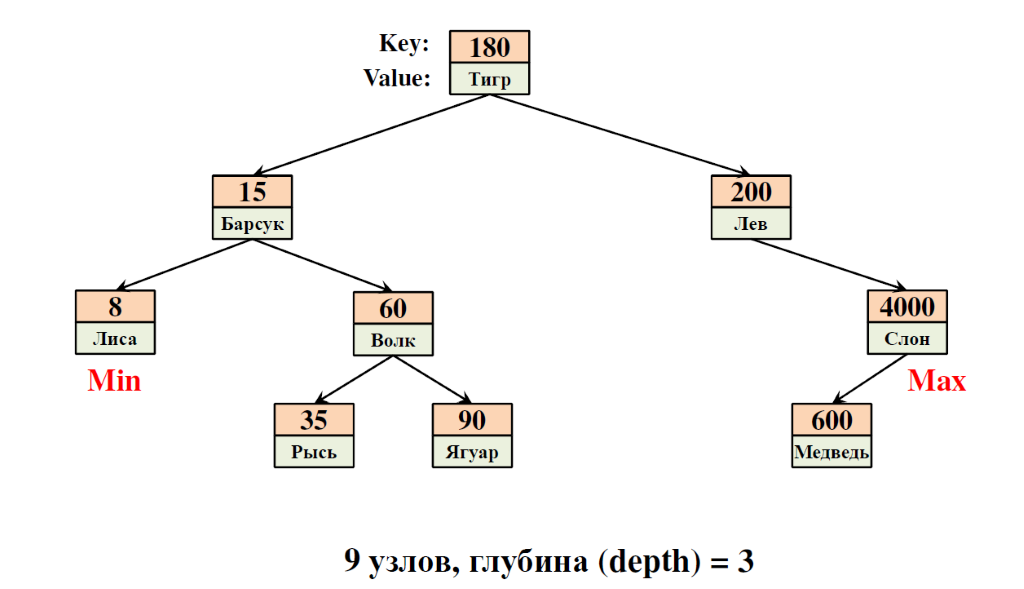
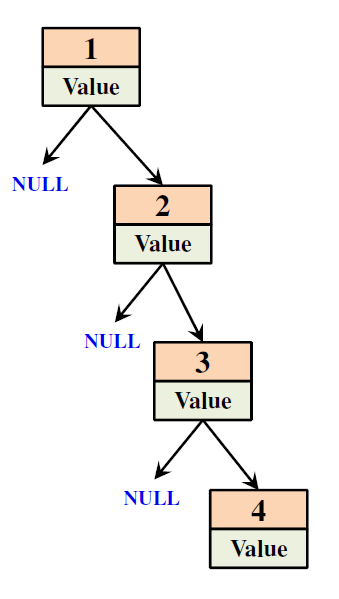
Красно-чёрные деревья. Красночёрные деревья Двоичные деревья поиска (Binary search Tree, bst)
 Скачать 0.62 Mb.
|
Красно-чёрные деревья |
| Операция | Средний случай (average case) | Худший случай (worst case) |
| Add(key, value) | O(log n) | O(log n) |
| Lookup(key) | O(log n) | O(log n) |
| Remove(key) | O(log n) | O(log n) |
| Min | O(log n) | O(log n) |
| Max | O(log n) | O(log n) |
Сложность по памяти: O(n)
Применение красно-черных деревьев
GNU libstdc++ (/usr/include/c++/bits)
std::map, std::multimap, std::set, std::multiset
LLVM libc++
std::map, std::set
Java
java.util.TreeMap, java.util.TreeSet
Microsoft .NET 4.5 Framework Class Library
SortedDictionary, SortedSet
Красно-черное дерево (Red-blacktree, RB-tree) – это бинарное дерево поиска, для которого выполняются красно-черные свойства (red-black properties):
Каждый узел является красным или черным
Корень дерева является черным
Каждый лист дерева (NULL) является черным
У красного узла оба дочерних узла – черные
У любого узла все пути от него до листьев, являющихся его потомками, содержат одинаковое кол-во черных улов
Пример красно-черного дерева
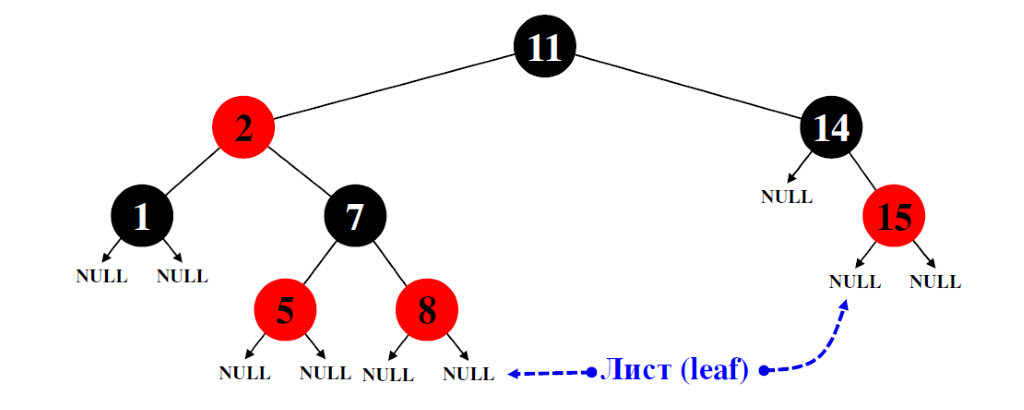
Добавление элемента
Находим лист для вставки нового элемента
Создаем элемент и окрашиваем его в красный цвет
Перекрашиваем узлы и выполняем повороты
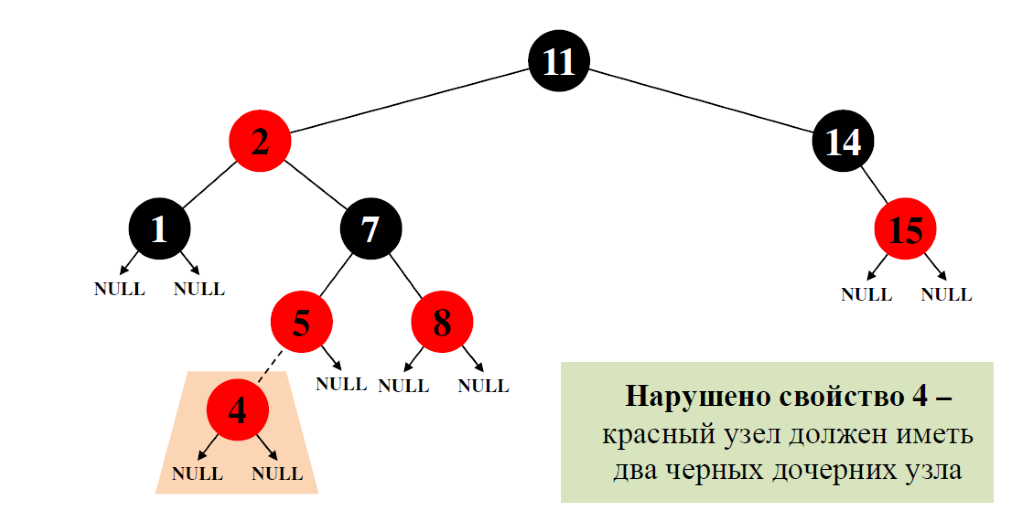
Нарушение свойств красно-черного дерева
Какие свойства красно-черного дерева могут быть нарушены после вставки нового узла (красного цвета)?
Каждый узел является красным или черным – выполняется
Корень дерева является черным – не выполняется (например, при добавление первого элемента)
Каждый лист дерева (NULL) является черным – выполняется
У красного узла оба дочерних являются черными – не выполняется
У любого узла все пути от него до листьев (его потомков), содержат одинаковое число черных узлов – выполняется (новый узел замещает черный NULL, но сам имеет два черных дочерних NULL)
После добавления нового элемента свойства 2 и 4 могут быть нарушены
Каждый узел является красным или черным – выполняется
Корень дерева является черным – не выполняется (например, при добавление первого элемента)
Каждый лист дерева (NULL) является черным – выполняется
У красного узла оба дочерних узла являются черными – не выполняется
У любого узла все пути от него до листьев, являющихся его потомками, содержат одинаковое число черных узлов – выполняется (новый узел замещает черный NULL, но сам имеет два черных дочерних NULL)
Восстановление красно-черного дерева
Возможно 6 случаев, нарушающих свойства красно-черного дерева (3 случая симметричны другим трем)
Восстановление свойств начинаем с нового элемента и продвигаемся вверх к корню дерева
Случай 1
Узел P – это корень левого поддерева своего родителя G
Узел z красный
Родительский узел P узла z красный
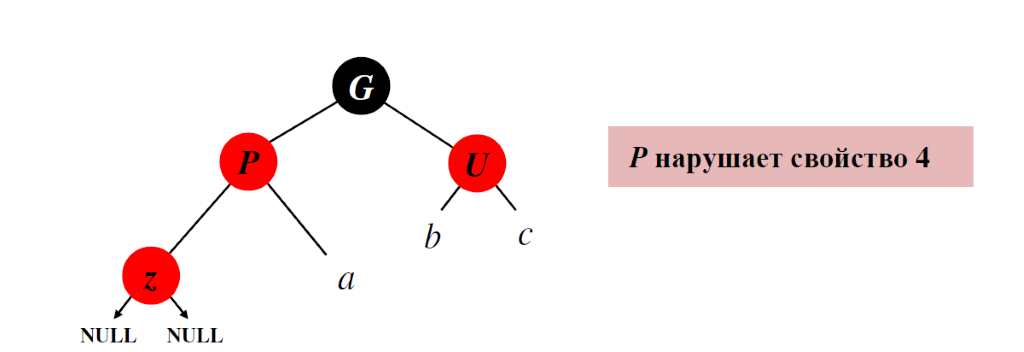Узел U (дядя узла z) красный Перекрашиваем узлы:
P – черный
U – черный
G – красный
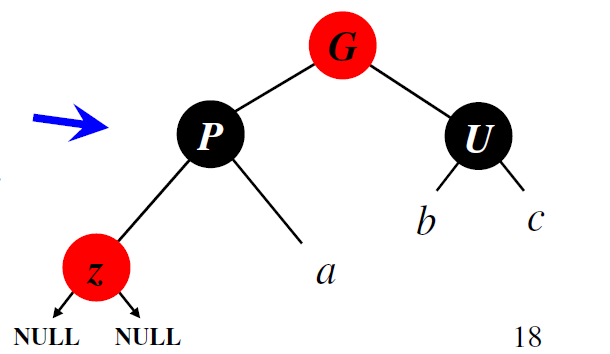
Случай 2
Узел P – это корень левого поддерева своего родителя G
Узел z красный
Родительский узел P узла z красный
Узел U черный
Узел z– правый дочерний элемент P
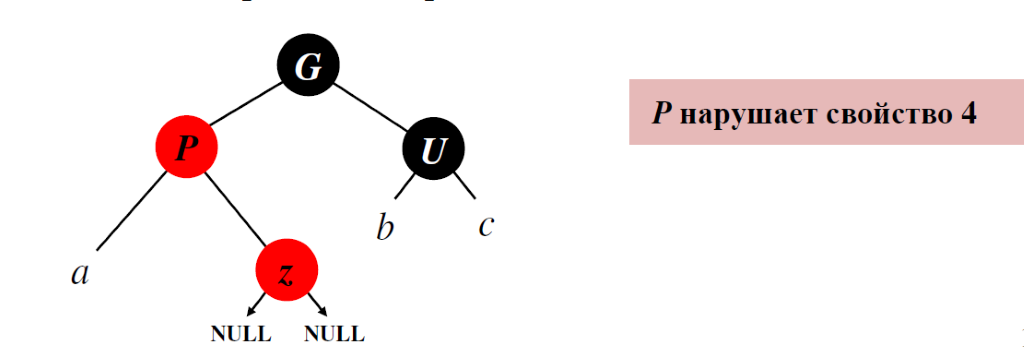
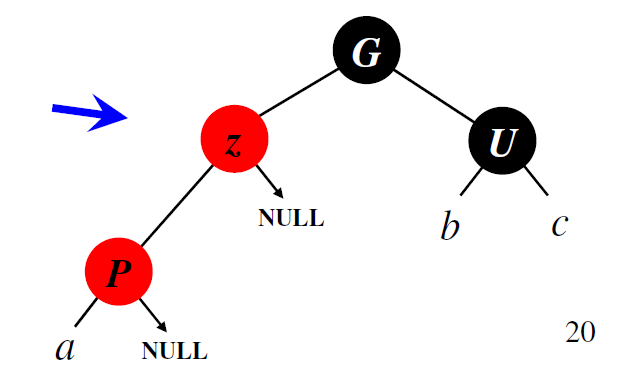Переходим к случаю 3 путем поворота дерева P влево Левый поворот дерева (leftrotation)
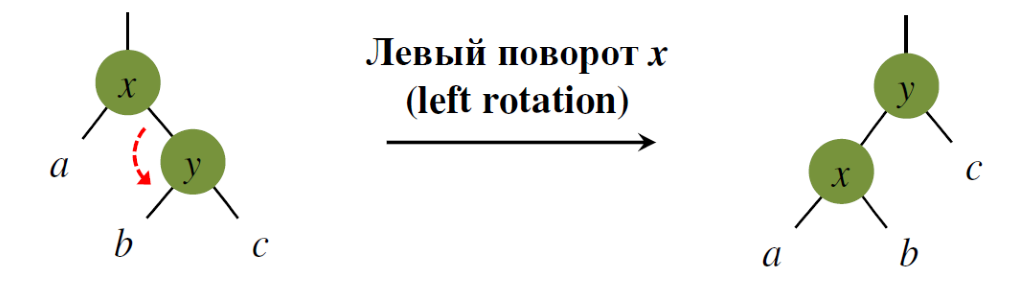
function LeftRotate(x)
y = x.right
x.right = y.left /* Subtree b */
if y.left != NULL then
y.left.parent = x /* Setup parent of b */
y.parent = x.parent
if x = x.parent.left then /* x is left subtree */
x.parent.left = y
else
x.parent.right = y
y.left = x
x.parent = y
end function
Случай 3
Узел P – это корень левого поддерева своего родителя G
Узел z красный
Родительский узел P узла z красный
Узел U черный
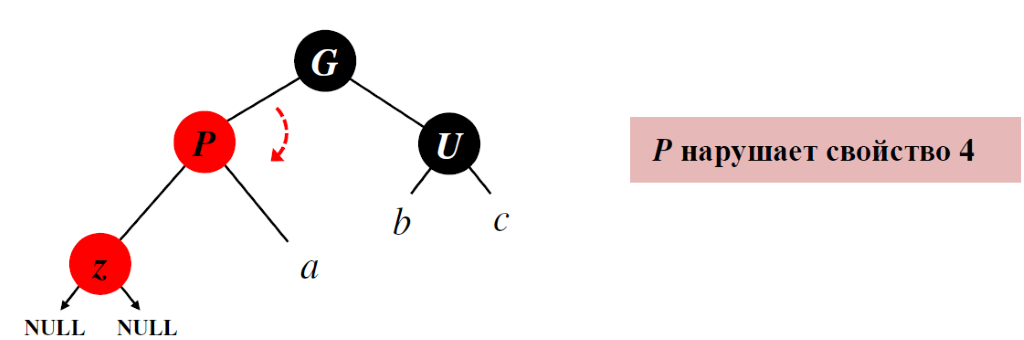Узел z– правый дочерний элемент P Перекрашиваем вершины:
P – черный
G – красный
Поворачиваем дерево G вправо
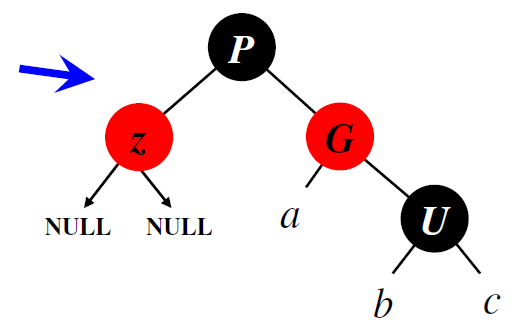
Правый поворот дерева (rightrotation)
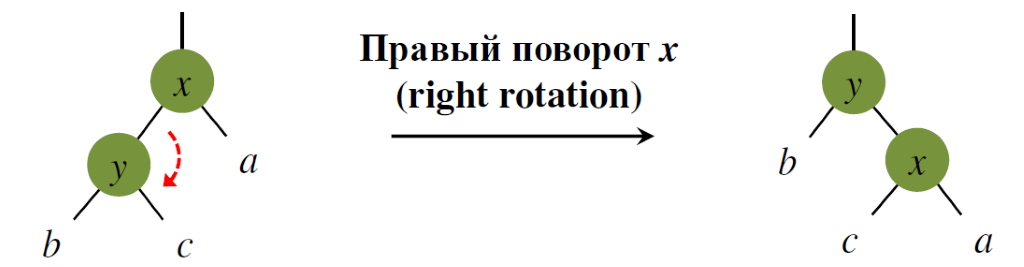
function RightRotate(x)
y = x.left
x.left = y.right /* Subtree c */
if y.right != NULL then
y.right.parent = x /* Setup parent of c */
y.parent = x.parent
if x = x.parent.left then /* x is left subtree */
x.parent.left = y
else
x.parent.right = y
y.right = x
x.parent = y
end function
Восстановление красно-черного дерева
Случаи 4, 5 и 6 симметричны случаям 1, 2 и 3
Узел P – это корень правого поддерева своего родителя G
Узел z красный
Родительский узел P узла z красный
Узел U черный или красный
Узел z– левый или правый дочерний элемент P
function RBTree_Fixup(z)
while z.parent.color = RED do
if z.parent = z.parent.parent.left then
/* z in left subtree of G */
y = z.parent.parent.right; /* Uncle */
if y.color = RED then
/* Case 1 */
z.parent.color = BLACK
y.color = BLACK
z.parent.parent.color = RED
z = z.parent.parent
else
if z = z.parent.right then
/* Case 2 --> case 3 */
z = z.parent
RBTree_RotateLeft(z)
end if
/* Case 3 */
z.parent.color = BLACK
z.parent.parent.color = RED
RBTree_RotateRight(z.parent.parent)
end if
else
/* z in right subtree of G */
/* ... */
end if
end while
root.color = BLACK
end function
Удаление элемента
По заданному ключу находим элемент для удаления
Удаляем элемент (как в случае обычного дерева поиска)
Перекрашиваем узлы и выполняя повороты восстанавливаем структуру красно-черного дерева
Высота красно-черных деревьев
Обозначим:
h(x) –высота красно-черного дерева с корнем в узле x
bh(x) – кол-во черных элементов на пути от узла x к листу («черная» высота дерева, black height)
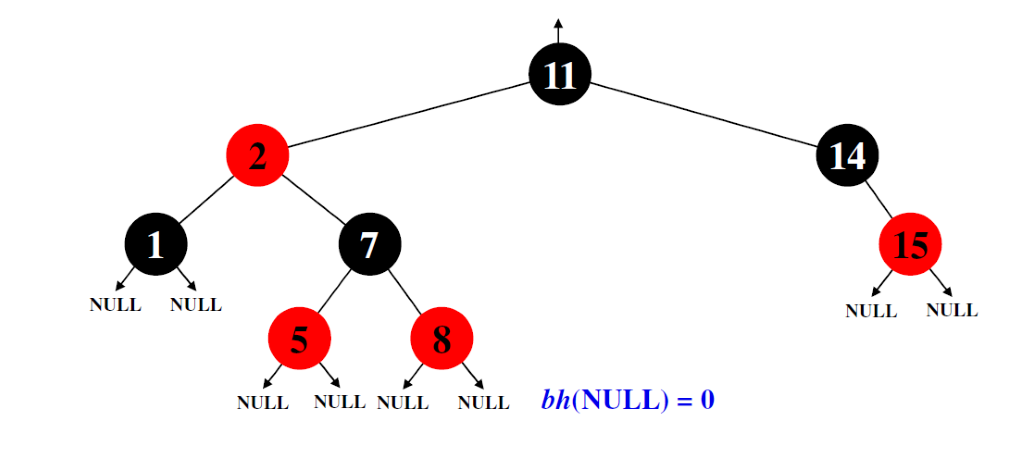
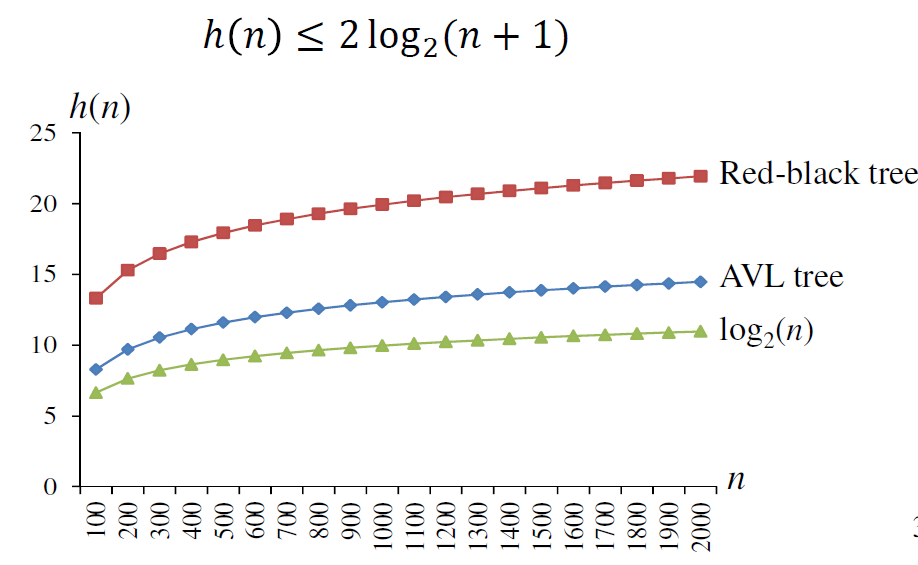
Лемма. Красно-черное дерево с nвнутренними узлами имеет высоту не более чем 2log(n+1)
Доказательство
Покажем по индукции, что любое поддерево с вершиной в узле xсодержит не менее 2bh(x) – 1 внутренних узлов
Базис индукции: bh(x) = 0, следовательно это лист (NULL, не содержит внутренних узлов): 20 – 1 = 0
Индуктивное предположение: считаем, в любом поддереве xс черной высотой < 2bh(x) – 1
Если xчерный, оба узла имеют черную высоту bh(x) – 1, если xкрасный, узлы имею высоту bh(x)
Следовательно в поддереве xчисло nвнутренних узлов
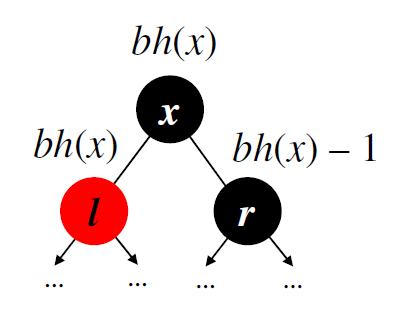
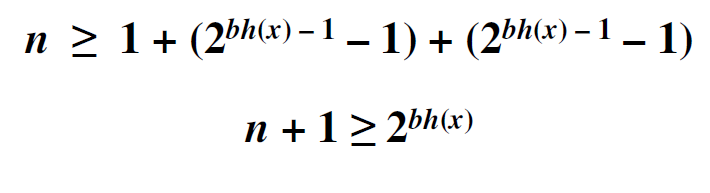
По свойства как минимум половина узлов на пути от корня к листу черный, тогда
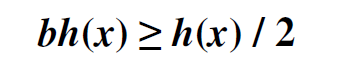
Следовательно
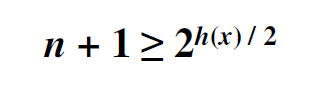
Логарифмируем
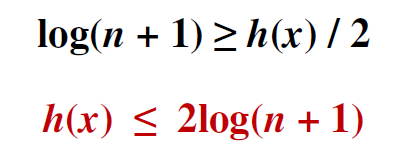
Red-black tree vs. AVL tree
Высота AVL-дерева
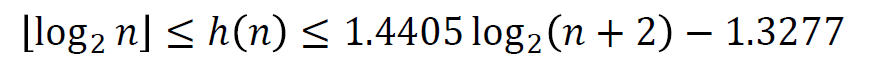
Высота красно-черного дерева
