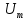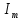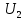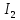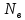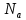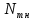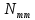контрольная работа по метрологии. метрология. Красноярский институт железнодорожного транспорта филиал федерального государственного бюджетного образовательного учреждения высшего образования Иркутский государственный университет путей сообщения
 Скачать 271.63 Kb. Скачать 271.63 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА федеральное государственное бюджетное образовательное учреждение высшего образования «Иркутский государственный университет путей сообщения» Красноярский институт железнодорожного транспорта - филиал федерального государственного бюджетного образовательного учреждения высшего образования «Иркутский государственный университет путей сообщения» Факультет «Заочное обучение и дополнительное профессиональное образование» Кафедра «Системы обеспечения движения поездов» Расчетно-графическая работа по дисциплине «Метрология, стандартизация и сертификация» РГР. 532120.23.05.05. – 2020
Содержание
Введение Характерная черта развития электроизмерительной техники на современном этапе – улучшение технико-экономических характеристик средств измерений. Существенно возросла точность измерительных приборов, повысилось их быстродействие, расширился диапазон измерения, увеличилось количество видов измеряемых величин. Современные измерительные приборы отличаются высоким уровнем автоматизации процесса измерения, что достигается благодаря использованию современной элементной базы, в том числе микропроцессоров. Однако эффективное использование средств измерений возможно только грамотными специалистами, владеющими методами измерений и знакомыми с соответствующими техническими средствами. Технологические процессы в различных отраслях промышленности, качество материалов и готовых изделий контролируются измерением неэлектрических величин с помощью электрических средств измерений, которые являются наиболее точными, универсальными и быстродействующими. Основная цель изучения дисциплины «Метрология, стандартизация и сертификация» – ознакомиться с основными понятиями метрологии и измерительной техники, теорией погрешностей, освоить методы и средства измерения электрических и неэлектрических величин во всем диапазоне изменения. При изучении дисциплины мы используем и закрепляем знания основных законов физики, электричества, механики, теоретических основ электротехники, высшей математики, статистики. В процессе изучения дисциплины мы получаем знания методов и техники выполнения измерений, принципов работы и устройства основных измерительных приборов и систем, приобретаем умения и навыки правильного выбора и использования того или иного средства измерения, обработки результатов измерений Задача 1 С помощью моста постоянного тока произведено 20 равноточных измерений сопротивления R i резистора. Полагая, что в приведенном ряду отсутствуют систематические погрешности, а случайные погрешности распределены по нормальному закону, определите: 1 Среднее арифметическое значение R ср математическое ожидание, результат измерения. 2 Среднеквадратическое отклонение σ результата отдельного измерения в данном ряду. 3 При наличии грубой погрешности промаха исключите результат измерения с грубой погрешностью, пользуясь правилом «3σ», и повторите расчёты по пунктам 1 и 2 для нового значения числа измерений 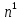 =n - m, где n=20 – количество измерений, m – количество промахов. =n - m, где n=20 – количество измерений, m – количество промахов.4 Среднеквадратическое отклонение S среднего арифметического. 5 Доверительный интервал DR ΔR=(tn S) при заданной доверительной вероятности P. Коэффициент Стьюдента t n возьмите из таблицы 2.1 по заданной доверительной вероятности P и количеству n измерений. Доверительный интервал DR округлите до двух значащих цифр. 6 Запишите результат измерения в виде R=Rср±ΔR при P = 0,99. 7 Постройте гистограмму распределения случайных погрешностей, взяв ширину интервалов 1= 0,5σ, где σ – среднеквадратическое отклонение, определённое в пункте 2. 8 Составьте алгоритм обработки результатов измерения. Вариант 4 Таблица 1 – Исходные данные
Доверительная вероятность Р = 0,95 Tп = 2,26 (3 вариант ) Решение 1 Среднее арифметическое значение Rср 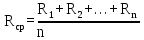 где 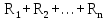 – результаты отдельных измерений; – результаты отдельных измерений;n – число измерений. 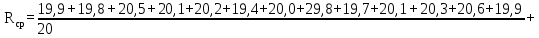 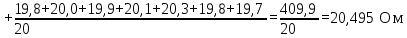 2 Среднеквадратическое отклонение σ результата отдельного измерения в данном ряду 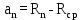 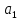 =19,9-20,495 =0,595 =19,9-20,495 =0,595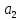 =19,8-20,495 =0,695 =19,8-20,495 =0,695 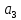 =20,5-20,495 =0,005 =20,5-20,495 =0,005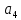 =20,1-20,495 =0,395 =20,1-20,495 =0,395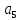 =20,2-20,495 =0,295 =20,2-20,495 =0,295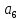 =19,4-20,495 =1,095 =19,4-20,495 =1,095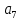 =20,0-20,495 =0,495 =20,0-20,495 =0,495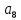 =29,8-20,495 =9,305 =29,8-20,495 =9,305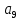 =19,7-20,495 =0,795 =19,7-20,495 =0,795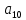 =20,1-20,495 =0,395 =20,1-20,495 =0,395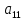 =20,3-20,495 =0,195 =20,3-20,495 =0,195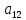 =20,6-20,495 =0,105 =20,6-20,495 =0,105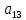 =19,9-20,495 =0,595 =19,9-20,495 =0,595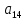 =19,8-20,495 =0,695 =19,8-20,495 =0,695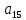 =20,0-20,495 =0,495 =20,0-20,495 =0,495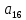 =19,9-20,495 =0,595 =19,9-20,495 =0,595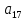 =20,1-20,495 =0,395 =20,1-20,495 =0,395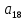 =20,3-20,495 =0,195 =20,3-20,495 =0,195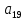 =19,8-20,495 =0,695 =19,8-20,495 =0,695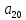 =19,7-20,495 =0,795 =19,7-20,495 =0,795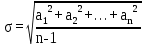 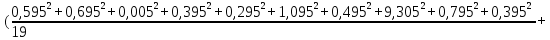 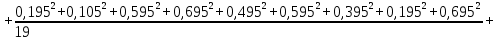 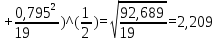 3 Исключение результата измерения с грубой погрешностью, пользуясь правилом «3σ» 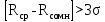 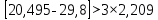 9,305  6,626 6,626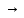 результат с грубой погрешностью результат с грубой погрешностью 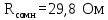 исключается и проводятся новые измерения по пунктам 1 и 2 исключается и проводятся новые измерения по пунктам 1 и 2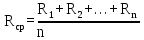 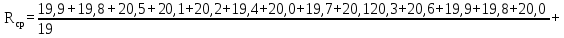 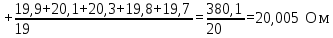 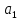 =19,9-20,005 =0,105 =19,9-20,005 =0,105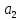 =19,8-20,005 =0,205 =19,8-20,005 =0,205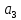 =20,5-20,005 =0,495 =20,5-20,005 =0,495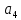 =20,1-20,005 =0,095 =20,1-20,005 =0,095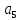 =20,2-20,005 =0,195 =20,2-20,005 =0,195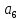 =19,4-20,005 =0,605 =19,4-20,005 =0,605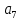 =20,0-20,005 =0,005 =20,0-20,005 =0,005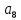 =19,7-20,005 =0,305 =19,7-20,005 =0,305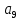 =20,1-20,005 =0,095 =20,1-20,005 =0,095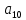 =20,3-20,005 =0,295 =20,3-20,005 =0,295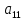 =20,6-20,005 =0,595 =20,6-20,005 =0,595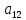 =19,9-20,005 =0,105 =19,9-20,005 =0,105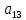 =19,8-20,005 =0,205 =19,8-20,005 =0,205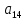 =20,0-20,005 =0,005 =20,0-20,005 =0,005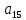 =19,9-20,005 =0,105 =19,9-20,005 =0,105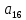 =20,1-20,005 =0,095 =20,1-20,005 =0,095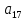 =20,3-20,005 =0,295 =20,3-20,005 =0,295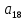 =19,8-20,005 =0,205 =19,8-20,005 =0,205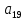 =19,7-20,005 =0,305 =19,7-20,005 =0,305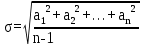 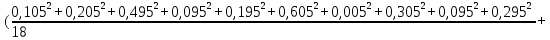 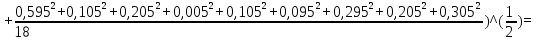 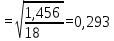 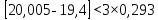 0,605 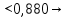 результат, принятый за результат, принятый за 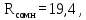 не является грубой погрешностью не является грубой погрешностью4 Среднеквадратическое отклонение S среднего арифметического 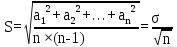 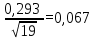 5 Определение доверительного интервала 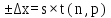 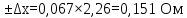 6 Окончательный результат 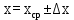 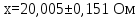 7 Построение гистограммы распределения случайных погрешностей Rmax=20,6 Ом, Rmin=19,4 Ом Размах результатов Р=Rmaх-Rmin 20,6 - 19,4 =1,2 Количество интервалов k=1+3,3  lg lg n=1+3,3 n=1+3,3 lg19=5,22 lg19=5,22 6 6Ширина интервалов 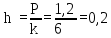 Начальное табличное значение 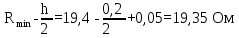 Таблица 2– Расчет гистограммы
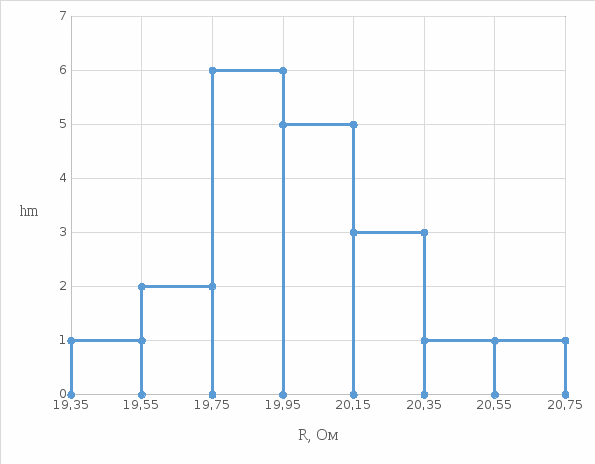 Рисунок 1– Гистограмма 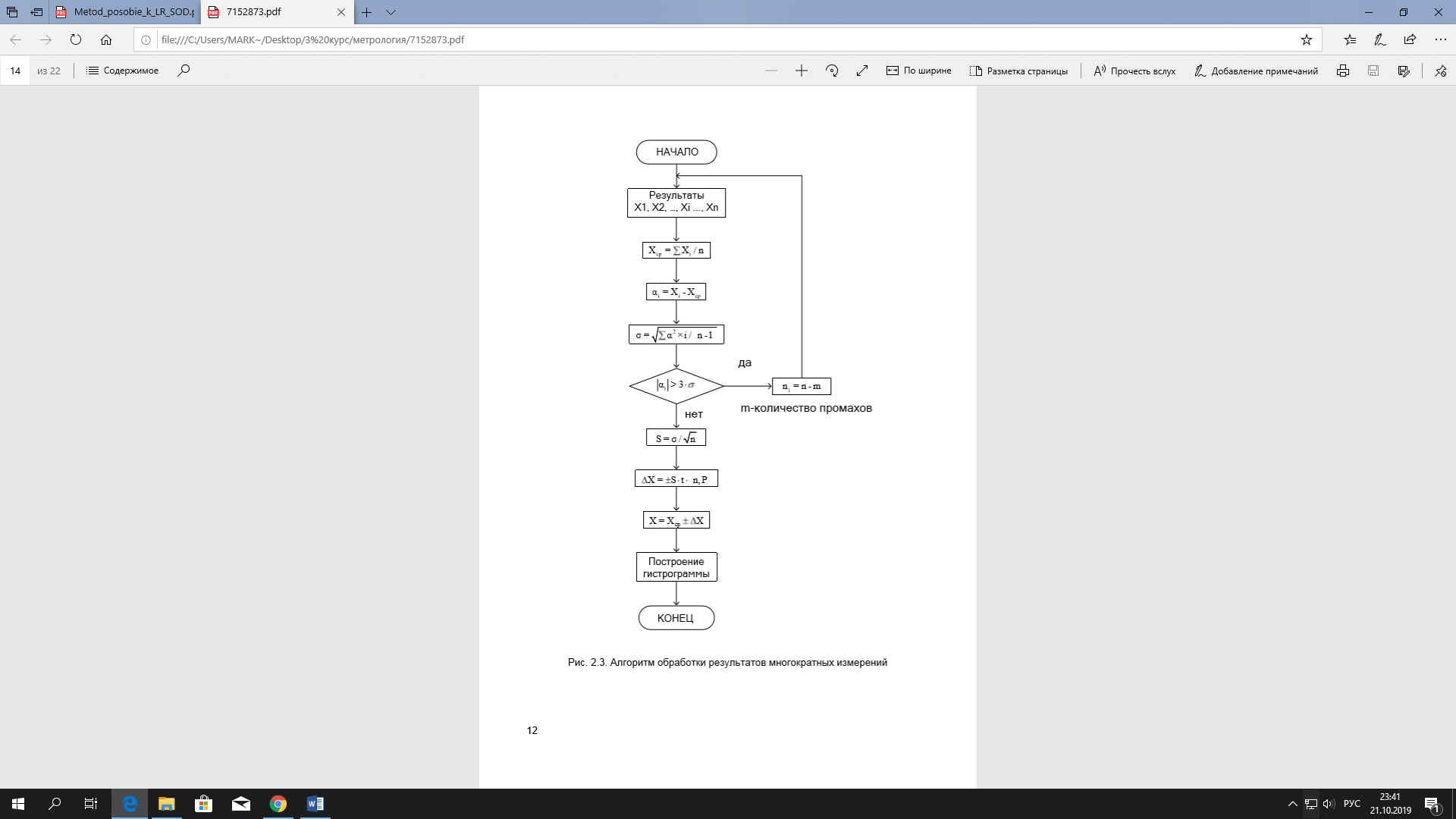 Рисунок 2 – Алгоритм обработки результатов многократных измерений Вывод: Полученная гистограмма соответствует «колоколу» Гаусса, что говорит о нормальном распределении результатов измерений напряжений, этим методом обрабатывать можно. Задача 2 Вероятностные оценки погрешности результата измерений на основании ряда наблюдений. Проведено пять независимых наблюдений одного и того же напряжения U. Найдите результат измерения и доверительную вероятность того, что абсолютная погрешность измерения не превышает по модулю ΔU. Систематической погрешностью можно пренебречь. Полагая, что в приведенном ряду систематической погрешностью можно пренебречь, а случайные погрешности распределены по нормальному закону, в данной задаче определите: 1 Среднее арифметическое значение Uср математическое ожидание, результат измерения. 2 Среднеквадратическое отклонение σ результата отдельного измерения в данном ряду. 3 При наличии грубой погрешности промаха исключите результат измерения с грубой погрешностью, пользуясь правилом «3σ», и повторите расчёты по п. 1 и 2 для нового значения числа измерений 1 n = n- m, где n = 5 – количество измерений, m – количество промахов. 4 Среднеквадратическое отклонение U среднего арифметического. 5 Доверительный интервал DR (ΔR=tnS) при заданной доверительной вероятности P. Коэффициент Стьюдента tn возьмите из таблицы по заданной доверительной вероятности P и количеству n измерений. Доверительный интервал DR округлите до двух значащих цифр. 6 Запишите результат измерения в виде U= Uср ± ΔU при P =0,95. 7 Определите, не превышает ли абсолютная погрешность по модулю ΔU. Вариант 4
 U = 25 мВ (по 3 варианту) U = 25 мВ (по 3 варианту)Решение 1 Среднее арифметическое значение Uср 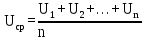 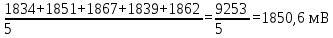 2 Среднеквадратическое отклонение σ результата отдельного измерения в данном ряду 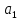 =1834-1850,6 =16,6 =1834-1850,6 =16,6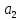 =1851-1850,6 =-0,4 =1851-1850,6 =-0,4 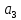 =1867-1850,6 =-16,4 =1867-1850,6 =-16,4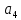 =1839-1850,6 =11,6 =1839-1850,6 =11,6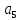 =1862-1850,6 =-11,4 =1862-1850,6 =-11,4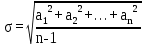 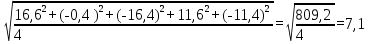 3 Исключение результата измерения с грубой погрешностью, пользуясь правилом «3σ» 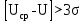 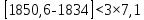 16,6 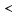 21,3 21,3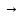 результат, принятый за результат, принятый за 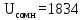 , не является грубой погрешностью. , не является грубой погрешностью.4 Среднеквадратическое отклонение S среднего арифметического 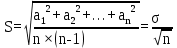 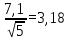 5 Определение доверительного интервала 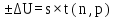 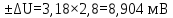 6 Окончательный результат 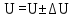 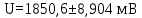 7 Абсолютная погрешность не превышает по модулю ΔU 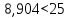 Вывод: Абсолютная погрешность измерения не превышает по модулю ΔU = 25 мВ. Задача 3. У вольтметра и амперметра с пределами измерений Uт и Iт, включенных соответственно через измерительные трансформаторы напряжения 6000/100 и тока 600/5, отсчет по шкале составил U2 и I2. Определите напряжение и ток в сети, а также предел допускаемой абсолютной и относительной погрешностей измерений, если известны классы точности приборов Nв и Na и измерительных трансформаторов Nтн и Nтт . Приведите схему измерения. Исходные данные для решения задачи 3 приведены в таблице 3 и таблице 4. 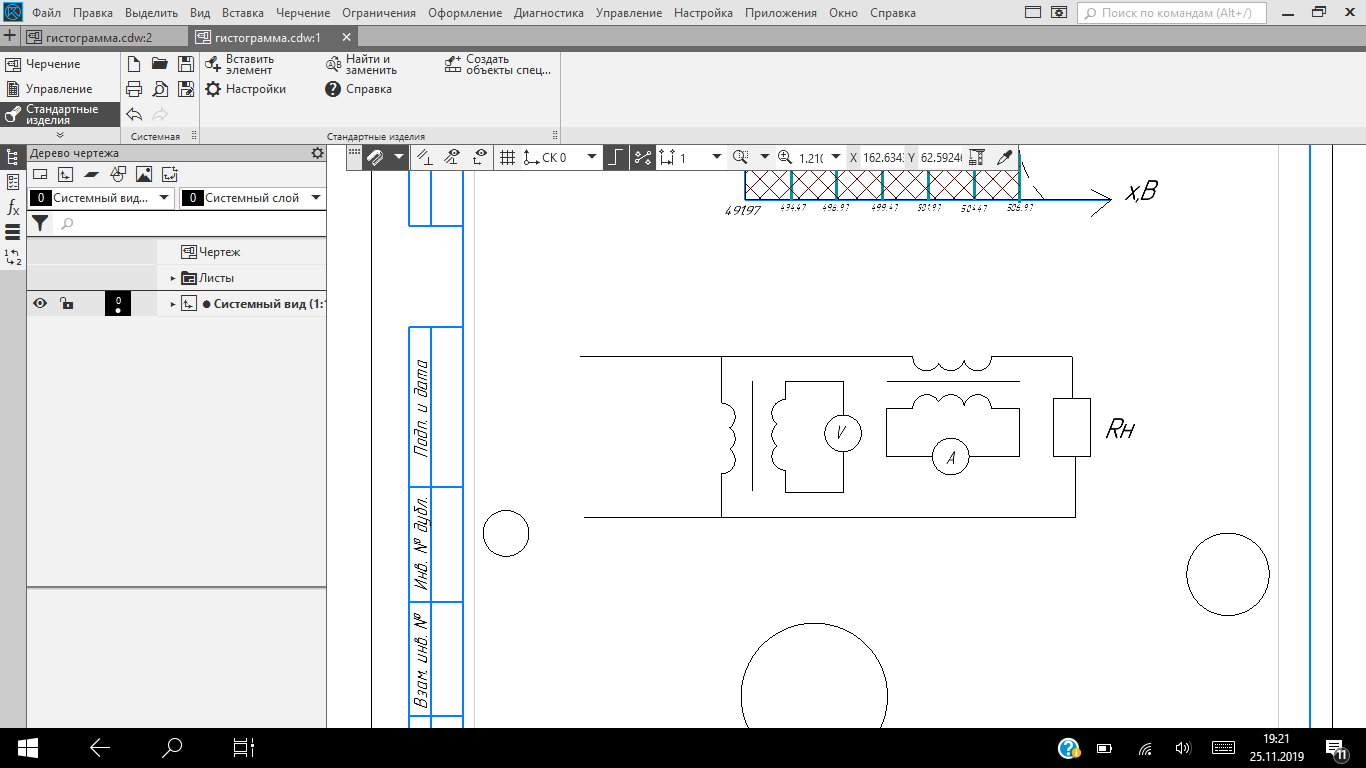 Рисунок-3 Схема измерения. Решение задачи 3 для варианта 4 и 3 . Рассмотрим формы аналитического выражения и способы нормирования пределов, допускаемых основной и дополнительной погрешностей средств измерений. Таблица 3 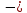 Данные для варианта Данные для варианта
Таблица 4 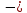 Данные для варианта Данные для варианта
1 Коэффициенты усиления трансформаторов 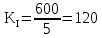 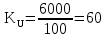 2 Определение тока и напряжения в сети 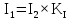 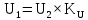 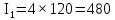 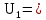 90 90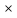 60=5400 60=54003 Определение абсолютной погрешности тока и напряжения 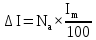 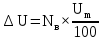 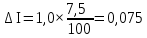 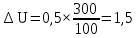 4 Определение абсолютных погрешностей коэффициентов трансформации 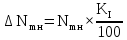 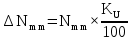 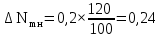 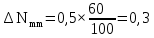 5 Результирующая абсолютная погрешность 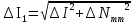 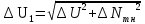 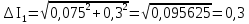 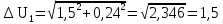 6 Относительная погрешность измерений 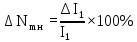 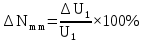 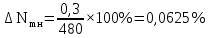 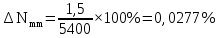 Вывод: В данной задаче были посчитаны коэффициенты трансформации для трансформаторов тока и напряжения, абсолютные погрешности амперметра и вольтметра, а также абсолютные и относительные погрешности тока и напряжения. Список использованных источников Летвинцев, В. Г. Методические указания и задания по выполнению контрольной работе./ В. Г. Литвинцев, Р.С. Трифонов. -М.: ЗабИЖТ, Чита, 2016. - 22 с. (Высшее образование) Димов Ю. В. Метрология стандартизация и сертификация: учеб. для вузов 3-е изд. / Ю. В Димов. – М,: Питер, 2010. – 464 с. (Высшее образование) Положение «Требование к оформлению текстовой и графической документации. Нормоконтроль» / Е. И. Михайлова. КрЖТИрГУПС, Красноярск, 2019. – 49 с. (Высшее образование) Красноярск 2020 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||