ЭРБ-20_Занченко_6_испр. Краткое теоретическое содержание
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
 Цель работы Исследовать зависимость момента инерции крестовины с надетыми на неё грузиками от распределения масс относительно оси вращения, проходящей через центр масс крестовины. Основные явления, изучаемые в работе: поступательное и вращательное движения тела. Краткое теоретическое содержание Маятник Обербека состоит из крестовины, на стержнях которой находятся грузы. Они могут перемещаться по стержням и закрепляться в нужном положении. Крестовина с грузами насажена на вал, на котором укреплены два шкива различного радиуса. На шкив намотана нить, которая переброшена через блок. К ее концу привязана гирька, момент силы тяжести которой уравновешивает момент сил трения. К концу нити подвешивают груз массой m, под действием силы тяжести которого система приводится в движение. На груз действует сила тяжести P=mg и сила натяжения F. При выводе расчетных формул лабораторной работы использованы законы динамики поступательного и вращательного движения твердого тела: Второй закон Ньютона для поступательного движения твердого тела: равнодействующая внешних сил F равна произведению массы m на ускорение тела a: 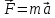 где 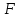 – сумма всех сил, приложенных к телу (Н); m- масса тела (кг); – сумма всех сил, приложенных к телу (Н); m- масса тела (кг); 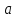 - линейное ускорение (м/с²). - линейное ускорение (м/с²).Основной закон динамики вращательного движения твердого тела: Момент вращающейся силы M, приложенной к телу, равен произведению момента инерции тела J на угловое ускорение 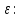 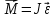 Где  - суммарный момент внешних сил, приложенных к телу относительно оси вращения(Н•м); J – момент инерции тела относительно той же оси (кг•м²); - суммарный момент внешних сил, приложенных к телу относительно оси вращения(Н•м); J – момент инерции тела относительно той же оси (кг•м²); 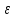 – угловое ускорение (м/с²). – угловое ускорение (м/с²).Определения: Поступательное движение - это такое движение, при котором прямая, соединяющая две любые точки тела, остается параллельной самой себе. Вращательным движением называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Моментом инерции материальной точки относительно некоторой оси называется величина, равная произведению масс материальной точки на квадраты её расстояние от оси, где масса материальной точки, расстояние от материальной точки до оси. Момент инерции твердого тела (сплошного) называется величина, равная произведению массы тела на радиус относительно оси, проходящей через центры оснований. Маятники - это твердые тела небольших размеров подвешенное на нерастяжимой нити масса которой пренебрежимо мала по сравнению с массой тело. Основные расчётные формулы Экспериментальное значение момента инерции:  где m – масса груза (кг), rо - радиус шкива (м), g - ускорение свободного падения (м/с2), h - путь, пройденный грузом за время t(м), t – время (с). Расчетный момент инерции: 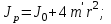 где  - масса одного груза на крестовине (кг), - масса одного груза на крестовине (кг),  - момент инерции грузов без крестовины (кг*м2), r – расстояние от оси вращения до центра масс грузов (м) - момент инерции грузов без крестовины (кг*м2), r – расстояние от оси вращения до центра масс грузов (м) где r²=xи 4m’=b, N – число опытов, Jᵢ - экспериментальные значения момента инерции 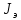 , полученные для каждого опыта, , полученные для каждого опыта,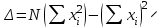 Формулы погрешностей косвенных измерений Абсолютная погрешность момента инерции маятника:  Дисперсия результата момента инерции: 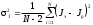 Схема 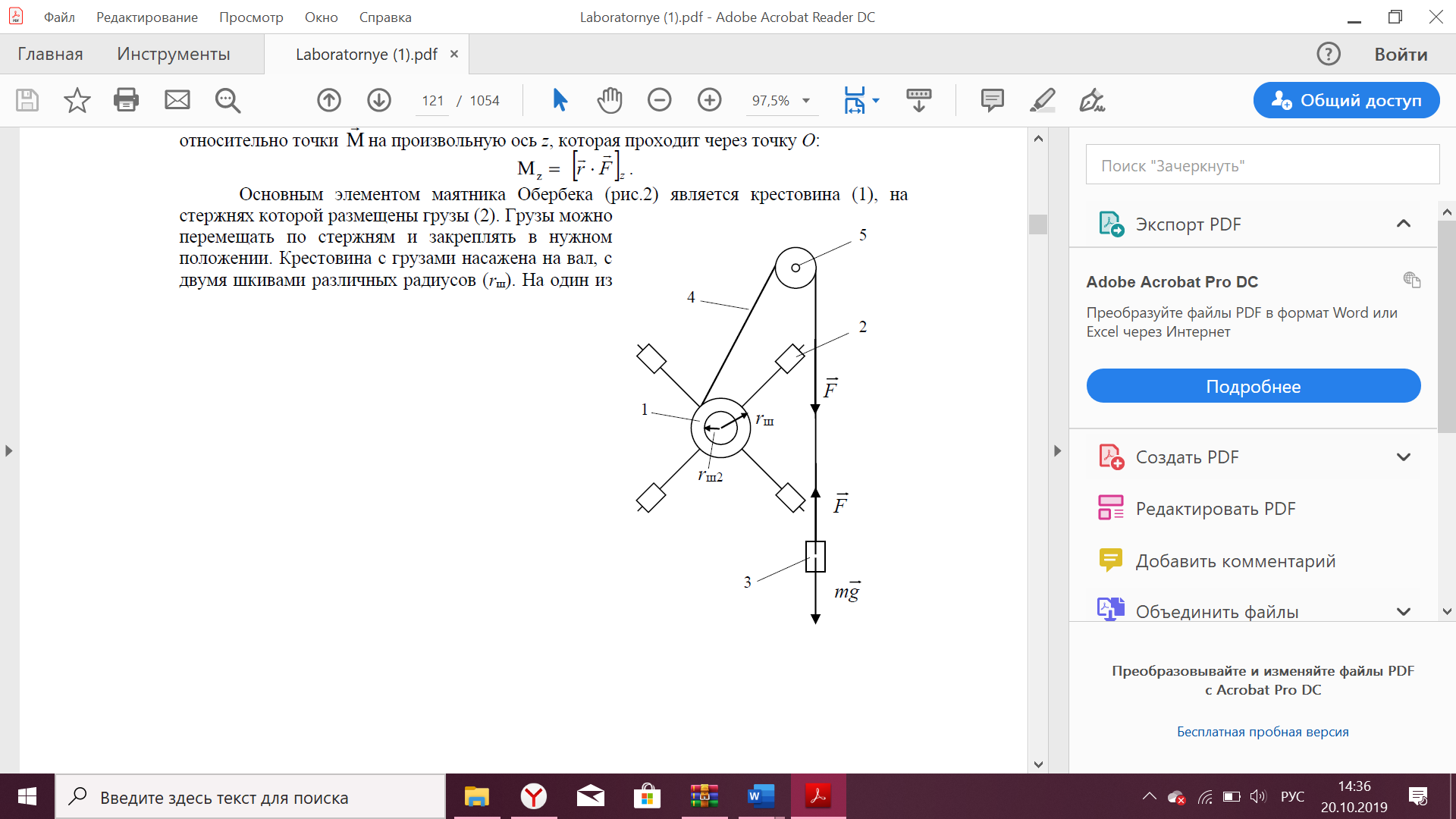 1) Крестовина; 1) Крестовина;2) Грузы; 3) Груз массой m; 4) Нить; 5) Блок. ТАБЛИЦА 1
ТАБЛИЦА 2
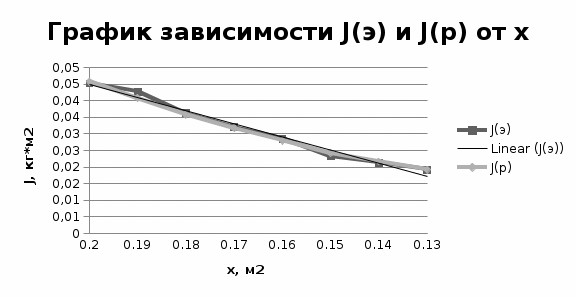 Примеры вычислений Исходные данные 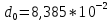 м - диаметр шкива; м - диаметр шкива; 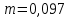 кг - масса груза; кг - масса груза;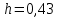 м - расстояние между рамками м - расстояние между рамками кг - масса грузов на стержнях кг - масса грузов на стержняхg = 9,8 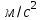 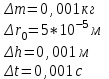 Расчёт для таблицы №1 (опыт 1)  - радиус шкива - радиус шкива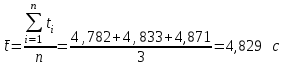 - время опыта - время опыта 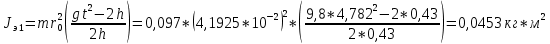 - экспериментальное значение момента инерции - экспериментальное значение момента инерции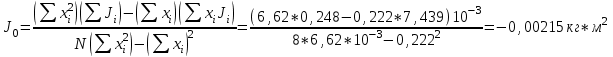 - - - момент инерции грузов без крестовины  Где Где  , ,  , N – число опытов, , N – число опытов,  - экспериментальное значение момента инерции, полученное для каждого опыта - экспериментальное значение момента инерции, полученное для каждого опыта - 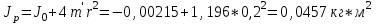 расчетный момент инерции расчетный момент инерцииРасчёт для таблицы №2 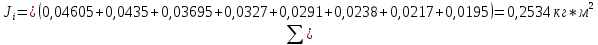 - сумма всех измерений момента инерции - сумма всех измерений момента инерции - радиус шкива в квадрате - радиус шкива в квадрате 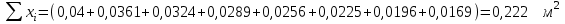 - - - сумма всех измерений радиуса шкива в квадрате 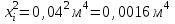 - квадрат радиуса шкива в квадрате - квадрат радиуса шкива в квадрате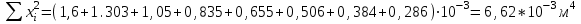 - сумма всех измерений квадрата радиуса шкива в квадрате - сумма всех измерений квадрата радиуса шкива в квадрате-  произведение радиуса шкива в квадрате и экспериментальное значение момента инерции произведение радиуса шкива в квадрате и экспериментальное значение момента инерции – сумма произведений радиуса шкива в квадрате и экспериментальное значение момента инерции – сумма произведений радиуса шкива в квадрате и экспериментальное значение момента инерции Расчёт погрешностей косвенных измерений 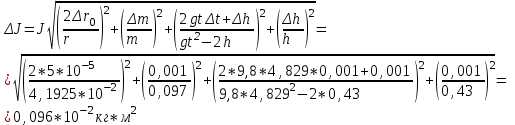 ΔJ - случайная погрешность измерения момента инерции ΔJ - случайная погрешность измерения момента инерции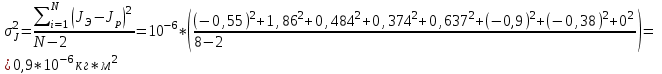  - дисперсия результата момента инерции - дисперсия результата момента инерции  - среднеквадратическим отклонением - среднеквадратическим отклонением Окончательный результат при r=0.2 м  Вывод В ходе лабораторной работы была исследована зависимость момента инерции крестовины с грузами от распределения массы относительно оси вращения, проходящей через центр масс. В результате измерений была получена прямо пропорциональная зависимость момента инерции от расстояния от оси вращения до центра масс груза. В процессе измерений были использованы штангенциркуль (для измерения диаметра шкива), линейка (для измерения расстояния от оси вращения до центра масс груза и расстояния между рамками), весы и секундомер. Полученное значение составляет разницу с табличным значением, равным 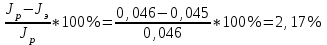 Поэтому можно говорить, что эксперимент проведён с достаточной точностью. |

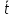
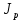
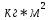
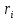
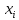




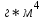
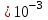
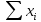 =0,222
=0,222 =0,2483
=0,2483 =0,662
=0,662
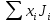 =7,439
=7,439