Массоотдача. Критериальное уравнение массоотдачи для неустановившегося процесса
 Скачать 64.11 Kb.
|
|
Приведите критериальное уравнение массоотдачи для неустановившегося процесса и при установившемся процессе в отсутствии влияния сил тяжести. Критериальное уравнение массоотдачи для неустановившегося процесса: 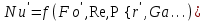 ,При установившемся процессе и при отсутствии влияния сил тяжести: 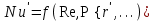 Выпишите формулы критерия Нуссельта, критерия Фурье, критерия Пекле, критерия Прандтля. Что они характеризуют? 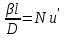 где l – определяющий геометрический размер. Данный безразмерный комплекс является аналогом теплового критерия Нуссельта и называется поэтому диффузионным критерием Нуссельта (иногда-критерием Шервуда Sh). Критерий Нуссельта 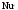 характеризует отношение скорости переноса вещества (конвективного и молекулярного) к молекулярному переносу.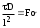 Диффузионный критерий Фурье (аналог теплового критерия Фурье), характеризует подобие неустановившихся процессов массообмена. 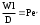 Диффузионный критерий Пекле (аналог теплового критерия Пекле) характеризует отношение переноса вещества конвекцией (W) к молекулярному переносу (D) в сходственных точках подобных систем. 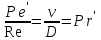 .Диффузионный критерий Прандтля 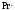 является аналогом теплового критерия (иногда критерий 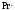называют критерием Шмидта Sc).Формально критерий 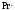выражает постоянство отношения физических свойств жидкости или газа в сходственных точках подобных систем. По существу же критерий 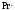характеризует отношение профиля скоростей (через ) к профилю концентраций (через D), то есть отношение толщины гидродинамического и диффузионного пограничных слоев.Выпишите выражение, с помощью которого можно найти соотношение между коэффициентами тепо- и массоотдачи, выведенное из обобщенного критериального выражения при одинаковых гидродинамических условиях. С помощью данного выражения можно найти соотношение между коэффициентами тепло- и массоотдачи: 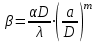 ,которое позволяет по известному значению, например , определить величину коэффициента массоотдачи при одних и тех же гидродинамических условиях. Основной смысл движущей силы массообменных процессов, что она характеризует? В соответствии со вторым законом термодинамики состояние замкнутой системы при взаимодействии двух фаз стремится к равновесию, что характеризуется равенством химических потенциалов компонентов фаз. Поскольку химические потенциалы неидеальных систем определить сложно, то при анализе и расчете процессов массопереноса рассматривают изменение концентраций компонентов. Процесс массопереноса протекает самопроизвольно при наличии разности между рабочими и равновесными концентрациями (при данных условиях температуры и давления), которые можно выразить через концентрации y и y* фазы y, а также x и x* для фазы x. Разность между рабочими и равновесными концентрациями и есть движущая сила массообменных процессов. Движущую силу в концентрациях фазы y будем выражать так: y = y – y* (при y > y*) или y = y* – y (при y < y*), а в концентрациях фазы x: x = x – x* или x = x* – x. Таким образом, движущая сила характеризует степень отклонения системы от равновесия. При установлении равновесия между фазами массообмен между ними прекращается. Почему находят среднюю движущую силу процесса? Запишите формулы средней движущей силы для двух контактирующих фаз. Так же как и при теплообмене, величина движущей силы массообменных процессов зависит от относительного направления движения фаз (противоток, прямоток и др.) Кроме того, на движущую силу большое влияние оказывает гидродинамическая структура потоков. Рассмотрим вариант, когда в массообменном аппарате фазы движутся противоточно по отношению друг к другу, аппарат работает в стационарном режиме по модели МИВ.  Полагаем, что перенос вещества происходит из фазы x в фазу y, то есть y < y*. Для этого случая линия равновесия располагается выше линии рабочих концентраций. 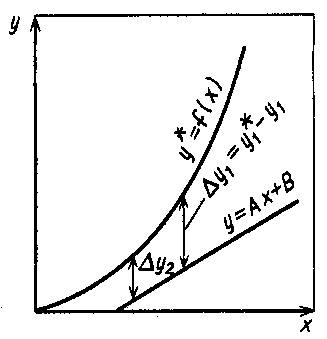 Для каждой точки или сечения аппарата y = y* – y, то есть получим y1, y2 и т.д. Для этого же варианта движущую силу выразим в концентрациях фазы x. 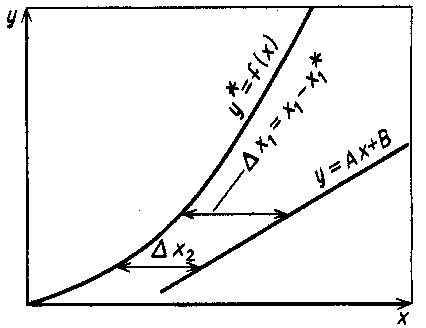 Тогда x = x – x*, то есть x1 = x1 – x1*, x2 и т.д. Отсюда видно, что движущая сила изменяется с изменением рабочей концентрации. Поэтому для всего процесса (или для всей поверхности F массопередачи) должна быть найдена средняя движущая сила. Для упрощения выводов полагаем, что аппарат работает по противоточной схеме при идеальном вытеснении, линия равновесия прямая (т.е. y* = m x), m > 1 и перенос вещества – из фазы x в фазу y. По аналогии с теплопереносом можно написать для массопереноса следующее выражение движущей силы процесса yср : – в концентрациях фазы y: 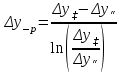 , 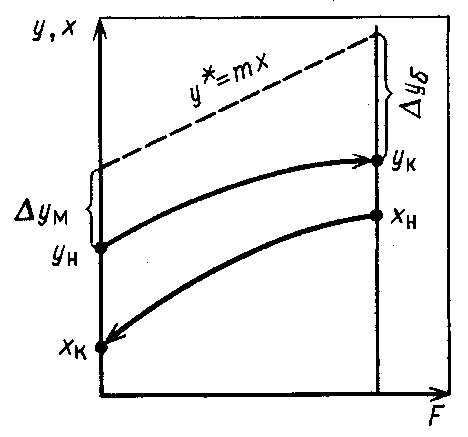– для фазы x 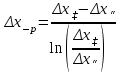 , 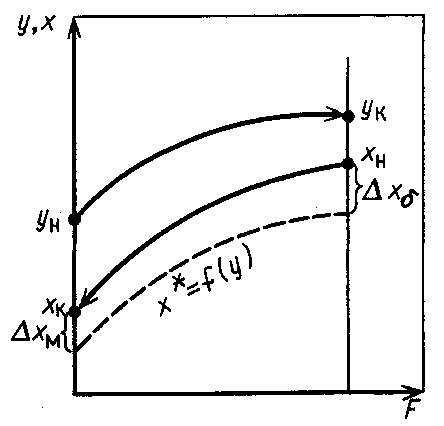где yб и xб – большая, а yм и xм – меньшая разности концентрации на концах массообменного аппарата. При 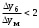 движущая сила может определяться как среднеарифметическая, то есть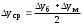 .Аналогичные выражения будут и для прямоточного движения фаз участвующих в массообмене. |