Паретто. Критерий Парето
 Скачать 2.57 Mb. Скачать 2.57 Mb.
|
|
Емельяненко В.А. Критерий Парето. Задачи многокритериального выбора, которые содержат не один, а сразу несколько критериев, представляют как теоретический, так и практический интерес, поскольку огромное число прикладных задач из области техники и экономики формализуются именно в многокритериальном виде. Согласно известному принципу Эджворта-Парето, всякий выбираемый вариант должен быть парето-оптимальным. К сожалению, в подавляющем числе многокритериальных задач множество Парето оказывается довольно широким, и конкретный выбор в его пределах не является очевидным. По этой причине и возникает проблема сужения множества Парето, связанная с выбором того или иного конкретного парето-оптимального варианта в качестве «наилучшего». Положительное решение этой проблемы представляет большой интерес для практики, поскольку в конкретных прикладных задачах выбора, как правило, следует ограничиться одним или же сравнительно узким количеством выбранных вариантов. Абстрактная задача выбора состоит в указании одного или нескольких вариантов из имеющегося исходного множества возможных (допустимых) вариантов (решений) X, которые называют выбираемыми. Будем обозначать множество всех выбираемых вариантов через C(X). Таким образом, в задаче выбора дано множество X, содержащее по крайней мере два элемента, а требуется найти некоторое его непустое подмножество C(X). Предполагается, что выбор производится неким лицом, принимающим решение (ЛПР), в роли которого может выступать как отдельный человек, так и целый коллектив, подчинённый достижению определённой цели. Для того чтобы совершаемый выбор в наибольшей степени соответствовал достижению имеющейся цели (т.е. был «наилучшим» или «оптимальным» для данного ЛПР), необходимо в процессе выбора учитывать «вкусы» и «предпочтения» ЛПР, которые в той или иной мере раскрывали бы смысл «наилучшего» решения. Иногда «предпочтения» ЛПР удаётся выразить каким-либо простым образом, например, так: вариант x′ предпочтительнее x′′ тогда и только тогда, когда оценка xf ′)( первого варианта строго больше (меньше) оценки xf ′′)( второго варианта, где f − заданная числовая функция, определённая на множестве X и называемая целевой функцией или критерием оптимальности. В таком случае множество C(X) будет состоять из элементов, доставляющих максимальное (минимальное) значение функции f на множестве X. При этом сама задача выбора превращается в обычную экстремальную (оптимизационную) задачу, которая хорошо изучена и для решения которой разработан широкий арсенал методов решения. Значительно более обширный (и интересный с точки зрения практики) класс задач выбора составляют те, в которых не удаётся выразить предпочтения ЛПР указанным выше простым способом. В этих задачах задаётся некоторый набор числовых целевых функций f1,..., fm, определённых на множестве X и образующих векторный критерий f = (f1,..., fm) со значениями в так называемом критериальном пространстве . При этом обычно добавляют, что для ЛПР каждый из этих критериев желательно максимизировать (или минимизировать). Последнее требование можно выразить более точно в форме так называемой аксиомы Парето, которая ниже формулируется применительно к задаче максимизации, рассматриваемой далее. Аксиома Парето звучит следующим образом: если оценка одного из двух вариантов не хуже оценки второго варианта по всем компонентам, причём по крайней мере по одной из них – строго лучше, то первый вариант предпочтительнее второго: Здесь символом обозначено бинарное отношение предпочтения ЛПР, определённое на X, а запись f X xx X ′ f ′′ означает, что из данной пары ЛПР выберет первый вариант и не выберет второй. К паре исходных объектов задачи (многокритериального) выбора X, f , как видим, добавилось ещё бинарное отношение предпочтения ЛПР . Сразу отметим, что при решении конкретных задач выбора отношение обычно полностью не известно (в отличие от X и f), поэтому принятие ЛПР аксиомы Парето означает наличие некоторой информации об этом отношении. Такая информация даёт возможность из пары вариантов f X f X ′, xx ′′, подчиняющихся условию в левой части импликации (1), исключить второй вариант как «заведомо негодный». В общем случае вариант, не выбираемый в некоторой паре, может оказаться выбранным из всего множества X. Однако при решении достаточно широкого класса задач можно считать выполненным следующее предположение. Аксиома исключения. Вариант, не выбираемый в какой-либо паре, не должен оказаться среди выбранных и из исходного множества возможных вариантов, т.е. 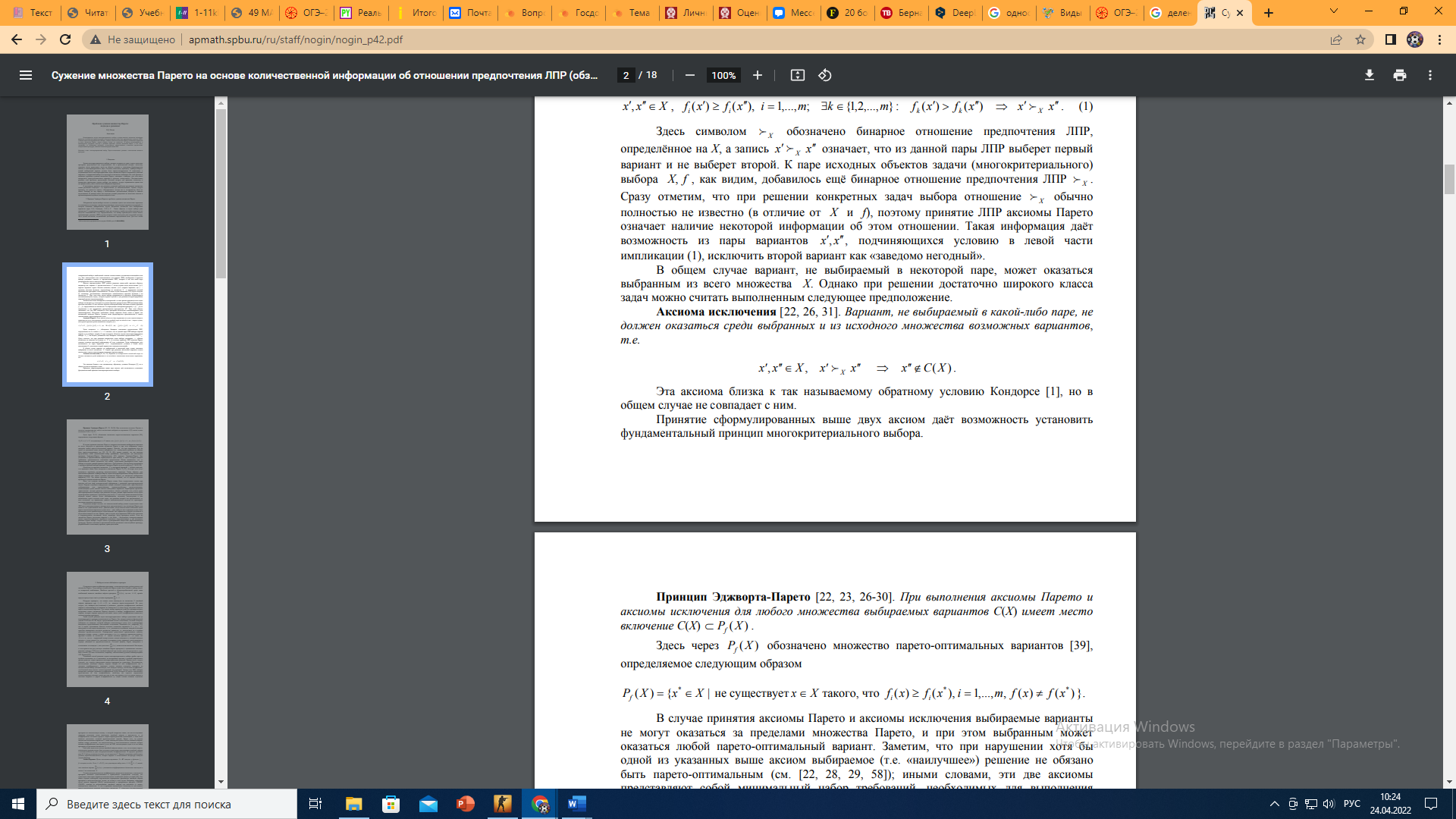 Эта аксиома близка к так называемому обратному условию Кондорсе [1], но в общем случае не совпадает с ним. Принятие сформулированных выше двух аксиом даёт возможность установить фундаментальный принцип многокритериального выбора. Перейдем к принципу Эджворта-Парето. При выполнения аксиомы Парето и аксиомы исключения для любого множества выбираемых вариантов C(X) имеет место включение C(X) 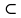 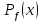 Здесь через обозначено множество парето-оптимальных вариантов, определяемое следующим образом: Здесь через обозначено множество парето-оптимальных вариантов, определяемое следующим образом:В случае принятия аксиомы Парето и аксиомы исключения выбираемые варианты не могут оказаться за пределами множества Парето, и при этом выбранным может оказаться любой парето-оптимальный вариант. Заметим, что при нарушении хотя бы одной из указанных выше аксиом выбираемое (т.е. «наилучшее») решение не обязано быть парето-оптимальным, иными словами, эти две аксиомы представляют собой минимальный набор требований, необходимых для выполнения принципа Эджворта-Парето. Первоначально принцип Эджворта-Парето был установлен в предположении справедливости трёх аксиом, в число которых входило требование транзитивности отношения предпочтения. Позже выяснилось, что от транзитивности можно отказаться; тем самым, существенно расширился класс задач выбора, в которых данный принцип «работает». Своё развитие (для нечётких отношений и в терминах функций выбора) принцип Эджворта-Парето получил в работах. Поскольку на практике множество X и векторный критерий f обычно известны, то в принципе может быть построено и множество Парето, хотя при этом могут возникнуть серьёзные трудности вычислительного характера. Таким образом, при выполнении принципа Эджворта-Парето задача многокритериального выбора может быть сформулирована как задача сужения множества Парето до множества выбираемых вариантов C(X). Эта задача оказалась настолько сложной, что её нередко именуют проблемой сужения множества Парето. Ясно, что сужение множества Парето может быть осуществлено только при наличии той или иной дополнительной информации о решаемой многокритериальной задаче. Нередко подобную информацию авторы заменяют какими-либо эвристическими соображениями или определёнными «правдоподобными» предположениями, позволяющими сузить область поиска «наилучших» вариантов. Характерным признаком эвристических методов является невозможность чёткого описания того класса задач многокритериального выбора, при решении которых данный эвристический метод будет гарантированно приводить к желаемому результату. С этой точки зрения аксиоматические подходы можно считать более обоснованными, поскольку используемая в них аксиоматика строго отделяет класс задач, для решения которых она предназначена, от всех остальных, где применение данного аксиоматического подхода не гарантирует получение желаемого результата. Отдельные авторы считают, что окончательный выбор должно осуществлять само ЛПР после непосредственного анализа всего представленного ему множества Парето или какой-то его существенной части. Действительно, когда имеется лишь небольшое число парето-оптимальных вариантов (лучше всего – два), выбор из них в принципе может быть произведён после сравнительного сопоставления этих вариантов и анализа достоинств и недостатков каждого из них. Правда, даже в случае двух вариантов ЛПР может оказаться в затруднительном положении, когда, например, число критериев велико. Если же множество Парето достаточно широкое, а тем более, − бесконечное, непосредственный анализ парето-оптимальных вариантов становится затруднительным и для успешного решения задачи выбора следует иметь в распоряжении какую-либо формализованную процедуру. Краткое описание и критический анализ различного типа подобных процедур, разработанных к настоящему времени, приводится ниже. |
