Разбор урока 6 класс. 6 класс разбор задачи-ключ по ролям. Куб, объем куба
 Скачать 299.96 Kb.
|
|
6 класс. Разбор по ролям задачи на тему «Куб, объем куба» Мотивация к деятельности – Здравствуйте, ребята. Вы познакомились с методом ролей решения математической задачи. Сегодня вы будете этим методом решать олимпиадную задачу. Давайте вспомним, какие роли бывают? (Называют роли) Для повторения ролей рассмотрите таблицу. ▲Учитель показывает таблицу. 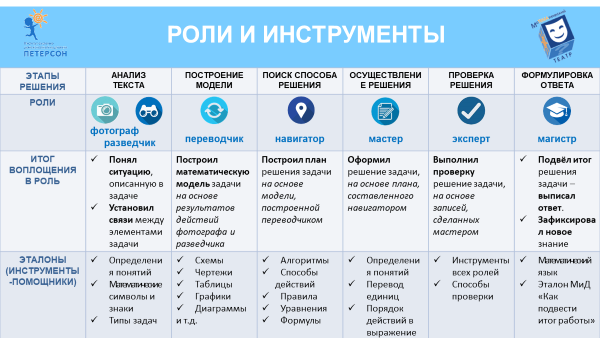 Я знаю, что Рома чемпион в спид-кубинге и собирает кубик Рубика за 15 секунд. А давайте вспомним, что мы с вами изучили про такие объемные тела, как прямоугольный параллелепипед и куб? (Ребята отвечают) Что показалось вам наиболее интересным в этой теме? (отвечают, вспоминаем задание про ВПР) 2. Актуализация имеющихся знаний Давайте рассмотрим кубик Рубика! На какое число маленьких кубиков он разделен? (отвечают) А как можно это найти, мы же не видим те кубики, которые внутри? (рассказывают про объем) А если разделить кубик на большее число маленьких кубиков? Каким оно может быть? Можно ли разделить куб на 8 одинаковых кубиков? А на 10? А почему? - Теперь, когда вспомнили эту тему, давайте попробуем решить олимпиадную задачу: 3. Пробное действие Кубик склеен из маленьких деревянных кубиков. В нем просверлили 6 сквозных дырок, параллельных ребрам (см. рис.) Сколько маленьких кубиков осталось неповрежденными? 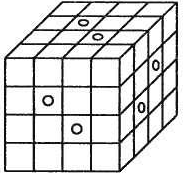 ▲ Школьники в течение 2 минут решают задачу в парах. После этого учитель спрашивает ответ. Учитель просит ученика, предложившего верный ответ, рассказать о своих рассуждениях. Начало возможного рассуждения ученика. – Возможное рассуждение ученика Конец возможного рассуждения ученика. – Можем ли мы сказать, каким методом решил задачу @Имя? – Теперь давайте попробуем решить эту задачу методом ролей. ▲На слайде презентации появляются иконки ролей.  – Что узнал фотограф? (Кубик состоит из маленьких одинаковых кубиков. Отверстия параллельны ребрам (большого куба? маленьких кубиков?).) – На всех ли важных условиях сфокусировал взгляд внутренний фотограф ˂Пети˃? (Нет. Важное условие, что отверстия сквозные) – На чём ещё обязательно должен остановить свой взгляд фотограф? (На том, что нужно найти в задаче — число неповрежденных кубиков) – Верно. Далее разведчик оглядывает внутренним взором поле своего опыта решения задач. На какие задачи похожа данная задача? Как решаются эти задачи? (Эта задача на подсчет числа маленьких кубиков в большом кубе. На объем куба. Нужно рассмотреть маленькие кубики отдельно.) – В игру вступает переводчик. Напомните, что должен сделать переводчик? (Перевести условие задачи на математический язык. Он составляет модель задачи – уравнение.) – Поднимите правую руку те ученики, которые представляют, какое будет уравнение, и что нужно для его составления. Левую руку поднимите те ученики, которые пока не чётко представляют уравнение. Итак, ваш внутренний переводчик почувствовал затруднение. проговорите в паре своё затруднение. Кто может его озвучить? (Не могу составить уравнение по этой задаче.) 4. Фиксация затруднения – Какая причина вашего затруднения? (Не знаю, как составить уравнение по данным задачи, когда столько переменных введено.) 5. Постановка цели деятельности – Какова будет цель деятельности? (Научиться применять десятичную запись при составлении уравнения в решении задач на нахождение цифр многозначного числа.) – Ребята, ваш переводчик немного потерялся. Что делает человек, когда теряется в лесу или чужом городе? (Останавливается, осматривается, старается успокоится и составить план дальнейших действий.) 6. Составление и осуществление плана деятельности – Согласна с вами. У вас на партах лежат конверты с полосками, на которых написаны вопросы, ответив на которые получатся пункты плана действий. На этих полосках нет номеров. Постарайтесь ответить на эти вопросы и выложить ответы в нужном порядке, работая в парах. ▲ В конверте лежат полоски с вопросами. Ученики выкладывают их по порядку и сверяются с порядком вопросов на слайде.  – Ребята, перевоплотитесь в переводчиков. Вам в помощь вопросы. Отвечая на них, составьте уравнение по условию задачи. ▲На слайде презентации появляются ответы на вопросы и образец уравнения по задаче: Искомое число можно обозначить, используя десятичную запись    ИЛИ возможны другие ответы, приводящие к другому уравнению. Искомое число можно обозначить х   – Ребята, наш переводчик – мастер своего дела, составил 2 уравнения по одной задаче. Какое уравнение вам кажется проще? (Второе.) – Давайте поработаем со вторым уравнением методом ролей. Следующая роль навигатора. Теперь вы навигаторы, которые знают последовательность шагов решения уравнения. Что скажет навигатор мастеру? (Ответы детей.) – Вы правы. Навигатор сообщает мастеру, что уравнение, содержащее переменную в обеих частях уравнения, можно решать … Продолжите предложение. (Методом весов.) – В чём заключается метод весов? (Он заключается в том, что из левой и правой части уравнения можно вычесть одно и то же число или выражение.) – Поработайте мастерами и примените метод весов к решению уравнения 4х = х + 321 и через минуту сверьте своё решение с образцом. 4х = 3х = 321 найдём множитель х, разделив произведение 321 на 3 х = 321 : 3 х = 107  ▲На слайде презентации появляется подробный образец решения уравнения. – Можно ли выписывать ответ? (Нет, так как не сделана проверка.) – Верно, ещё не проведена экспертиза. Перевоплощаемся в экспертов. Как можно выполнить проверку правильности решения? (Подставить полученное число в исходное уравнение.) – Этим самым мы что проверим? (Правильность решения уравнения.) – Но если уравнение составлено не верно, то эта проверка будет не полной проверкой решения задачи. Перевоплотитесь в роль магистра. Он видит картину решения в целом. Как ещё проверить, что число 107 – искомое число? (Проверить его на выполнение условий задачи. 1+3=4, 0+2=2, 7+1=8. 428:107=4.) – Вы правы. Прочтите ещё раз вопрос задачи и скажите, о чём должен подумать наш внутренний магистр? (Нужно найти все такие числа.) – Все ли числа найдены? (Уравнение имеет только один ответ, значит других чисел нет.)  1 + 3 = 4, 0 + 2 = 2, 7 + 1 = 8. 428 : 107 = 4 Вывод эксперта: число 107 является единственным решением задачи, можно выписывать ответ. Ответ. Это число 107 ▲На слайде презентации появляется образец проверки. нужно упростить это уравнение, потом посмотреть, что можно сделать с новым – Ребята, какую модель задачи мы ещё не рассмотрели? (Первое уравнение.) – Правильно. Именно магистру интересно поработать и с этим уравнением. Он понимает, что, решая его, вы закрепляете метод весов, используете десятичную запись числа для решения олимпиадной задачи. Я вам предлагаю заполнить таблицу перевоплощения во все роли при решении задачи с использованием первого уравнения. Затем сверьте свои рассуждения и записи с подробным образцом на слайде презентации. Таблица внутреннего диалога в роли переводчика, навигатора, мастера и эксперта
–Какое бы вы дали название задачам, которые мы решили? (Например: «О числах», «Секреты чисел», «Десятичная запись», «Десятичная запись помогает находить числа» или «Десятичная запись- ключ к загадке».) ▲ Выбирается лучшее название, которое понравится всем. Условно назовем эту тему «Десятичная запись». – Попробуйте заполнить пропуски в советах по решению задач:  Советы по решению задач на нахождение цифр неизвестного числа Если в задаче есть число с неизвестными цифрами, то каждую из них можно обозначить ____________: Для составления уравнений в таких задачах можно использовать десятичную запись числа:  , и так далее. Так как a, b, c, … – цифры, то такое уравнение называется уравнением ______________.Для решения уравнения в цифрах можно воспользоваться методом _____________ и свойствами ______________________. 7. Фиксация нового знания в виде Советов и проговаривание в устной речи  ▲ Школьники заполняют пропуски и согласовывают вставки. Учитель демонстрирует итоговый эталон и просит проговорить советы вслух:Советы по решению задач на нахождение цифр многозначного числа Если в задаче есть число с неизвестными цифрами, то каждую из них можно обозначить переменной/буквой: Для составления уравнений в таких задачах можно использовать десятичную запись числа: Для решения уравнения в цифрах можно воспользоваться методом перебора и свойствами делимости. 8. Самостоятельная работа с самопроверкой по образцу ▲ Учитель может предложить решить самостоятельно с использованием метода ролей любую из задач. 1. Удивительные делители Таня нашла трехзначный и семизначный делители числа 173173173, не раскладывая его на простые множители. Найдите такие делители и вы. 2. Из начала в конец Десятичная запись трехзначного числа начинается с цифры 9. Если первую цифру этого числа перенести в конец записи, то получится трехзначное число на 216 меньше первоначального. Найдите эти числа. 3. Единицы и десятки Вера загадала трехзначное число и поменяла у него местами две последние цифры. Потом сложила получившееся число с исходным. В результате получилось число 1387. Какое число могла загадать Вера? 4. Возраст джинна Возраст джинна выражается шестизначным числом вида 5. Только сумма Андрей сложил два двузначных числа и получил 147. Потом он записал оба числа в обратном порядке и вычислил сумму получившихся чисел. Какой могла оказаться эта сумма? | |||||||||||||||||||||||||||||||||||||
