Лекции и практики (1). Курс лекций и материалы для практических занятий

• Название: Курс лекций и материалы для практических занятий
• Дата: 17.03.2023
• Размер: 1.01 Mb.
• Имя файла: Лекции и практики (1).docx
• Тип: Курс лекций; #996812
• страница: 25 из 75

Способы организации индексов

Существует множество способов организации индексов:

1. 
   В плотных индексах для каждого значения ключа имеется отдельная запись индекса, указывающая место размещения конкретной записи. Неплотные (разреженные) индексы строятся в предположении, что на каждой странице памяти хранятся записи, отсортированные по значениям индексируемого ат- рибута. Тогда для каждой страницы в индексе задаётся диапазон значений ключей хранимых в ней записей, и поиск записи осуществляется среди запи- сей на указанной странице.
   
2. 
   Для больших индексов актуальна проблема сжатия ключа. Наиболее распро- страненный метод сжатия основан на устранении избыточности хранимых данных. Последовательно идущие значения ключа обычно имеют одинако- вые начальные части, поэтому в каждой записи индекса можно хранить не полное значение ключа, а лишь информацию, позволяющую восстановить его из известного предыдущего значения. Такой индекс называется сжатым.
   
3. 
   Одноуровневый индекс представляет собой линейную совокупность значе- ний одного или нескольких полей записи. На практике он используется ред- ко. В развитых СУБД применяются более сложные методы организации ин- дексов. Особенно эффективными являются многоуровневые индексы в ви- де сбалансированных деревьев (B-деревьев, balance trees).
   

2. Многоуровневые индексы на основе В-дерева

B-дерево строится динамически по мере заполнения базы данными. Оно растёт вверх, и корневая вершина может меняться. Параметрами B-дерева яв- ляются порядок n и количество уровней. Порядок – это количество ссылок из вершины i-го уровня на вершины (i+1)-го уровня. Пример построения B-дерева порядка 3 приведён на рис. 5.5.

Рис. 5.5. Пример построения B-дерева порядка 3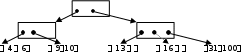

Каждое B-дерево должно удовлетворять следующим условиям:

1. 
   Все конечные вершины расположены на одном уровне, т.е. длина пути от корня к любой конечной вершине одинакова.
   
2. 
   Каждая вершина может содержать n адресных ссылок и (n-1) ключей. Ссыл- ка влево от ключа обеспечивает переход к вершине дерева с меньшими зна- чениями ключей, а вправо – к вершине с большими значениями.
   
3. 
   Любая неконечная вершина имеет не менее n/2 подчинённых вершин. (Для деревьев нечётного порядка значение n/2 округляется в большую сторону).
   
4. 
   Если неконечная вершина содержит k (k) ключей, то ей подчинена (k+1) вершина на следующем уровне иерархии.
   

Алгоритм формирования B-дерева порядка n предполагает, что сначала заполняется корневая вершина. Затем при появлении новой записи корневая вершина делится, образуются подчинённые ей вершины. При запоминании каждой новой записи поиск места для неё начинается с корневой вершины. Ес- ли в существующем на данный момент B-дереве нет места для размещения но- вого ключа, происходит сдвиг ключей вправо или влево, если это невозможно – осуществляется перестройка дерева.


В качестве конкретного примера рассмотрим индексирование в виде B- дерева, которое используется в СУБД Oracle (рис. 5.6).

Рис. 5.6. Пример индексного блока СУБД Oracle
Организация индексов в СУБД Oracle несколько отличается от рассмот- ренной выше классической организации B-дерева, но принцип остаётся тот же: одинаковое количество уровней на любом пути и автоматическая сбалансиро- ванность. Верхние блоки индекса содержат автоматически вычисляемые значе- ния, которые позволяют осуществлять поиск данных. Предпоследний (n-1)-й уровень содержит значения индексируемого поля (атрибута) без повторов (т.е. каждое значение один раз). Самый нижний n-й уровень – блоки-листья, кото- рые содержат индексируемые значения и соответствующие идентификаторы записей RowID (row identification, КБД), используемые для нахождения самих записей. Для неуникальных индексов значения идентификаторов строк (RowID) в блоках-листьях индекса также отсортированы по возрастанию. Блоки-листья связаны между собой двунаправленными ссылками.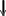

Поиск по ключу осуществляется следующим образом. Блок верхнего уровня (уровень 1) содержит некоторое значение X и указатели на верхнюю и нижнюю части индекса. Если значение искомого ключа больше X, то происхо- дит переход к верхней части индекса (по левому указателю), иначе – к нижней части. Блоки второго и последующих уровней (кроме двух последних) хранят начальное X₀ и конечное значения X_к ключа, а также три указателя. Если значе- ние искомого ключа меньше, чем X₀, то происходит обращение по левому ука- зателю; если оно больше, чем X_к, то происходит обращение по правому указа- телю; если оно попадает в диапазон X₀X_к – по среднему указателю. Вершины, которые делят следующий уровень дерева на три поддерева, могут занимать несколько уровней. Это зависит от количества индексируемых записей и сред- него размера индексируемых значений.

При обнаружении значения искомого ключа в блоке индекса происходит обращение к диску по RowID и извлечение требуемой записи (записей). Если же значение не обнаружено, результат поиска пуст.


Индекс в виде B-дерева автоматически поддерживается в сбалансирован- ном виде. Это означает, что при переполнении какого-либо из блоков индекса происходит перераспределение значений ключей индекса (без физического пе- ремещения записей данных). Например, если при добавлении новой записи с ключом "Горин" возникает переполнение соответствующего блока индекса (рис. 5.6), система может перестроить индекс так, как показано на рис. 5.7.

Рис. 5.7. Пример перераспределения данных индексного блока СУБД Oracle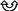
Если все блоки-листья индекса заполнены приблизительно на три четвер- ти, то при добавлении новой записи автоматически осуществляется полная пе- рестройка B-дерева путём введения дополнительного уровня.

Структура B-дерева имеет следующие преимущества:

• 
  Все блоки-листья в дереве расположены на одном уровне, следовательно, поиск любой записи в индексе занимает примерно одно и то же время.
  
• 
  B-дерево автоматически поддерживается в сбалансированном виде.
  
• 
  B-деревья обеспечивают хорошую производительность для широкого спек- тра запросов, включая поиск по конкретному значению и поиск в открытом и закрытом интервалах (благодаря ссылкам между блоками-листьями).
  
• 
  Модификация данных таблицы выполняется достаточно эффективно, т.к. в блоках индекса обычно есть свободное место для размещения новых значе- ний, а полная перестройка дерева выполняется достаточно редко.
  
• 
  Производительность B-дерева одинаково хороша для маленьких и больших таблиц, и не меняется существенно при росте таблицы.