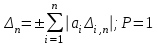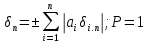ПИДР. 01 03 Косвенные измерения (1). Курс лекций метрология и Информационноизмерительная техника (М и иит) 2021 осень тема Основы метрологии фрагмент лекции
 Скачать 133.62 Kb. Скачать 133.62 Kb.
|
|
редакция 10.02.2022 г. Макарычев П.К. курс лекций: метрология и Информационно-измерительная техника (МиИИТ) 2021 осень тема 1. Основы метрологии … [ФРАГМЕНТ ЛЕКЦИИ] Косвенное измерения (КИ) это измерение, результат которого получают с использованием известной зависимости физической величины (функции) от нескольких других, значения которых могут быть получены прямыми измерениями. Простейшие типовые примеры представлены на рисунке 1.1.
Рисунок 1.1 – Примеры косвенных измерений … 1.2 Вычисление погрешностей косвенных измерений. Краткая теория Для вычисления погрешности КИ мы располагаем известной функциональной зависимостью результата Y от аргументов – результатов прямых измерений Х1, Х2,…, Хn: Y = f (Х1, Х2, … Хn) Требуется найти погрешность ΔY, возникающую от погрешностей ΔХ1, ΔХ2,… ΔХn. Упростим обозначения: ΔY = Δ; ΔХ1 = Δ1; ΔХ2 = Δ2; … ΔХn = Δn. Для решения нашей задачи в математике имеет место т.н. «формула полного дифференциала»:
Если мы используем при расчёте погрешности метод наихудшего случая (МНС), то предельное значение Δп в свёрнутой форме:
Примечание – Погрешности ∆i в проведённом эксперименте могут иметь как положительное значение, так и отрицательное. Эти знаки могут меняться от эксперимента к эксперименту. Используя МНС, мы выбираем наихудшие сочетания знаков: или все «плюс» или все «минус». Два частных случая позволяют формализовать решение практических задач по расчёту погрешностей КИ. Частный случай 1. Y = a1X1 + a2X2 +...+anXn = 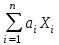 , ,т.е. Y – линейная функция аргументов Х1, Х2,…, Хn. Воспользуемся выражениями (1.1 и 1.2): 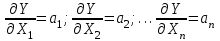 , следовательно, , следовательно,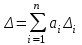 и и
Примеры: а) Y = X1 + X2; Р = 1. Здесь a1 = а2 = 1, тогда: Δ = 1Δ1 + 1Δ2; Для МНС: Δп = ± (|1Δ1,п| + |1Δ2,п|); б) Y = X1 – X2; Р = 1. Здесь a1 = 1; а2 = – 1, тогда: Δ = Δ1 – Δ2; Δп = ± (|1Δ1,п| + |1Δ2,п|); Полезный вывод: Δп для суммы и разности аргументов одинаковы. Частный случай 2. Y = X1a1·X2a2· … ·Xnan, где а1; а2;…аn – действительные числа, положительные или отрицательные, целые или дробные. Пример: Y = 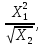 здесь а1 = 2; а2 = – 0,5. здесь а1 = 2; а2 = – 0,5.Частные производные: 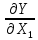 = =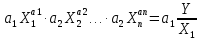 ; ;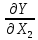 = =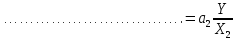 ………………………………………. 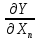 = =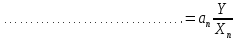 Далее: 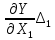 = =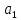 Y Y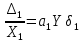 ; ;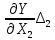 =…….. =……..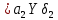 ; ;………………………. 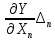 =…….. =……..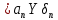 ; ;Следовательно, Δ = Y(a1δ1 + a2δ2 + ...+ anδn); δ = 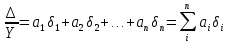 . .Предельное значение:
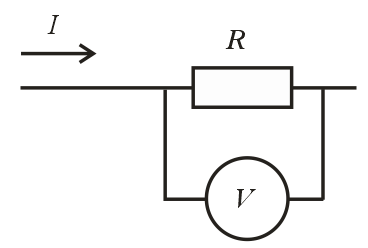
Забыли выкладки и используем только окончательное выражение (1.4) Примеры: а) Y = X1X2; P =1. Здесь: а1 = а2 = 1, тогда δ = 1δ1 + 1δ2; Для МНС имеем: δп = ± (|1δ1.п| + |1δ2.п|); б) Y = 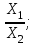 P =1 P =1Здесь: а1 = 1; a2 = – 1, тогда δ = 1δ1 – 1δ2; Для МНС имеем: δп = ± (|1δ1.п| + |1δ2.п|). Полезный вывод: δп для произведения и частного одинаковы. Объединяя наши четыре примера, можно сделать следующие выводы: для суммы и разности надо суммировать предельные значения абсолютных погрешностей аргументов, для произведения и частного – предельные значения относительных погрешностей аргументов. Несложный комплексный пример расчёта результата КИ. Рассмотрим для примера несложную абстрактную функцию Y = 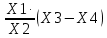 , где Хi – величины, значения которых известны с погрешностями ∆i.п*): , где Хi – величины, значения которых известны с погрешностями ∆i.п*):Х1 = Х1±∆1.п Х2 = Х2±∆2.п Х3 = Х3±∆3.п Х4 = Х4±∆4.п Примечание – В общем случае Хi либо результаты прямых измерений, либо величины с нормированными значениями погрешностей, например, мера электрического сопротивления с известным допуском. Проведём расчёт погрешности косвенного измерения функции Y в соответствии с выражениями (1.3) и (1.4). Исходное выражение для погрешности функции запишем на основании (1.4): δу=δ1.п+δ2.п+δ(3+4).п= ∆1.п/Х1+∆2.п/Х2+ δ(3+4).п здесь использовано обозначение δ(3+4).п (∆3.п+∆4.п)/(Х3-Х4) Окончательно имеем: ∆у.п=[∆1.п/Х1+∆2.п/Х2+(∆3.п+∆4.п)/(Х3-Х4)] Х2/Х1(Х3-Х4) Осталось подставить значения и произвести расчёт. 1.3 Решение типовых задач Задание 1 Сопротивление резистора R измеряется с помощью миллиамперметра и вольтметра по схеме, представленной на рис. 1.2. 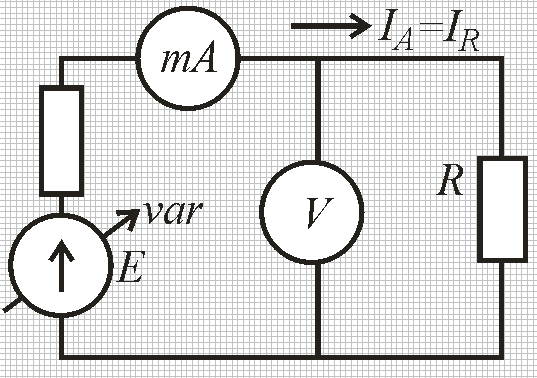 Рисунок 1.2 – Схема косвенного измерения сопротивления постоянному току Примечания 1 При реализации этой несложной схемы эксперимента следует помнить, что при протекании тока резистор нагревается в соответствии с законом Джоуля-Ленца. Выбирая режимы эксперимента, необходимо соблюдать условие: PRPRном/10, где PRном – номинальная мощность рассеивания резистора, которая записывается в его паспорте. В этом случае саморазогрев резистора хотя и приведёт к изменению его сопротивления, но изменение это не превысит заявленной погрешности его изготовления – допуска. Например, резистор типа С2-29 имеет паспортную мощность 1 Вт, номинальное сопротивление Rном = 10,0 кОм, производственный допуск ∆пр=±1,0 %, допустимая рассеиваемая мощность 100 мВт. 2 На практике изменяя Rвых, следует добиваться, чтобы один из приборов – амперметр или вольтметр – как получится, измерение осуществлял ближе к концу шкалы, тогда точность результата будет оптимизирована. Вывод: лучше, если в эксперименте будут использованы многопредельные приборы. Известны результаты измерений напряжения и тока: - результат прямого измерения напряжения UV UR =(10,030±0,050) В; Р=1; - результат прямого измерения силы тока IA IR =(1,000±0,025) мА; Р=1. Внутренние сопротивления измерительных приборов как у идеальных: у амперметра – ноль, у вольтметра – бесконечность. Требуется записать результат косвенного измерения R. Рассчитаем (косвенно измерим) значение сопротивления R: Rизм R=UR/IR = 10,030 В/1,000 мА = 10,03 кОм Далее рассчитаем погрешность полученного результата. В соответствии с (1.4) легко рассчитать относительную погрешность результата δп: δп = δV.п + δA.п = ± (0,050 /10,030 + 0,025/1,00) = ± (0,00499+0,025) ≈ ± 0,030 Теперь рассчитаем предельное значение погрешности результата в абсолютной форме: Δп = δп·R = 10,03 кОм × 0,030 = ±0,30 кОм Окончательно запишем результат измерения, как мы это уже привыкли делать: R=(10,03±0,30) кОм; Р = 1 (1.5) Задание 2 Как изменится результат косвенного измерения, полученный в задании 1, если стало известно, что внутреннее сопротивление вольтметра имеет значение, равное RV = 100 кОм±1%.? Решение. Ток, измеряемый миллиамперметром IA, является суммой двух токов: один протекает через измеряемый резистор IR (объект), а второй – через вольтметр IV (инструмент). Это показано на рис. 1.3. Второй ток вносит погрешность в измерение. Фактически используемая схема реализует косвенное измерение сопротивления параллельно включённых резистора R и входного сопротивления вольтметра RV. Примечание – Такие погрешности принято относить к погрешностям взаимодействия: взаимодействует инструмент (вольтметр) с объектом (резистором). 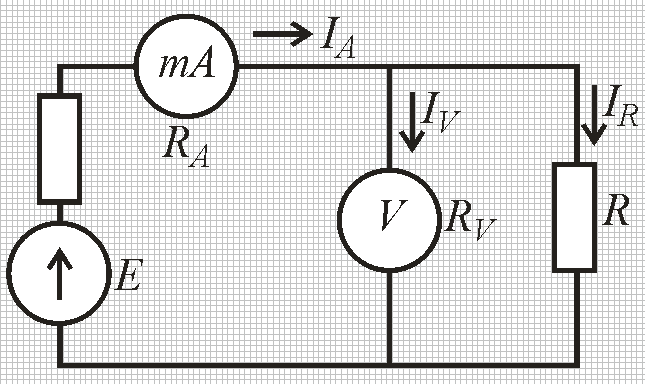 Рисунок 1.3 – Иллюстрация возникновения погрешности взаимодействия при косвенных измерениях сопротивления постоянному току Следуя высказанному наблюдению, делаем вывод, что в задании 1 мы измерили значение параллельно включённых R и RV: Rизм = (R·RV)/(R+RV) = (10,03±0,30) кОм. (1.6) Здесь погрешность чисто инструментальная: обусловлена метрологическими характеристиками использованных приборов. Однако нам необходимо рассчитать (косвенно измерить) значение R, которое выведем из (1.6): R=(RV·Rизм)/(RV-Rизм)=11,15 кОм. Рассчитаем погрешность. В соответствии с (1.4) имеем: δR.п= δRV.п+ δRизм.п+ δ(RV+Rизм).п, где δ(RV+Rизм).п=(∆RV.п+∆Rизм.п)/(RV-Rизм)=(1+0,30)/(100-10,03)=0,0144, тогда: δR.п =0,01+0,30+0,0144=0,32→∆R.п=RδR.п=11,150,32=3,57 кОм. Окончательно запишем результат: R=(11,2±3,6) кОм; Р=1 (1.7) Задание 3 Как изменится результат косвенного измерения R, полученный в задании 1, если измерения были проведены по альтернативной схеме, представленной на рис. 1.4? Известно значение входного сопротивления миллиамперметра RА=1,00 кОм±1,0%=1,00±0,01 кОм. 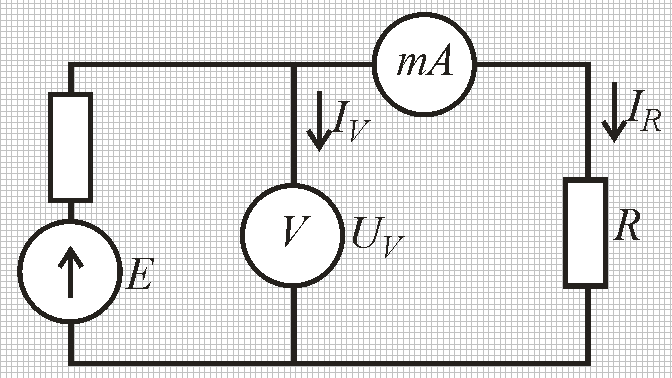 Рисунок 1.4 – Альтернативная схема косвенного измерения сопротивления R Заметим, что в данной схеме косвенно измеряется сопротивление последовательно включённых резистора R и резистораRА (входное сопротивление миллиамперметра): Rизм=R+RА = (10,03±0,30) кОм. (1.8) Откуда следует, что R = Rизм - RА = (10,03±0,30) кОм – (1,00 ±0,01) кОм = {закончить самостоятельно}. Самостоятельно сформулировать критерий выбора одной из двух схем измерения R(рис. 1.3 или 1.4), если известны RА и RV. Задание 4 Измерить косвенным методом ЭДС источника сигнала и записать результат в формате: Е = (ИЗ±∆п.); Р=1 исходные данные:
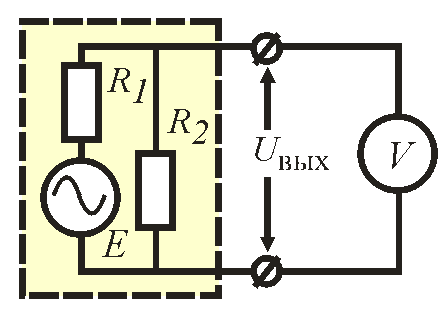
Схема измерения. Косвенно измерить силу тока в резисторе R2 и представить результат в виде I2=[ИЗ±∆п]; Р=1 Косвенно измерить падение напряжения в резисторе R1 и представить результат в виде U1=[ИЗ±∆п]; Р=1 Косвенно измерить Е=U2+U1 и представить в виде Е=[ИЗ±∆п] Примечание U2Uвых | ||||||||||||||||||||||||

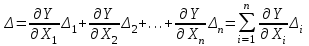
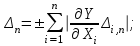 Р = 1.
Р = 1.