ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КУРС ЛЕКЦИЙ
СИНТЕЗ АВТОМАТИЧЕСКИХ ПРИБОРНЫХ УСТРОЙСТВ
Магистерская подготовка
«Системы ориентации, стабилизации и навигации»
Томск
|
ТЕОРЕТИЧЕСКИЙ МОДУЛЬ 2
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ АПУ
|
ЦЕЛИ МОДУЛЯ
1.Общие цели модуля
1.1. Изучить частотные характеристики АПУ и уметь использовать их при проектировании конкретных приборных устройств.
2.Частные цели модуля.
Изучив модуль, Вы сможете:
2.1. Давать определение:
2.2. Находить выражения:
Амплитудной частотной характеристики;
Фазовой частотной характеристики;
Логарифмических частотных характеристик.
2.3. Различать амплитудные и логарифмические частотные характеристики.
|
Частотные характеристики определяют реакцию системы (или звена) на гармоническое входное воздействие.
Частотные методы анализа и синтеза широко распространены в теории автоматического управления.
|
Если на вход системы (или звена) подаётся гармоническое воздействие с постоянной амплитудой и частотой
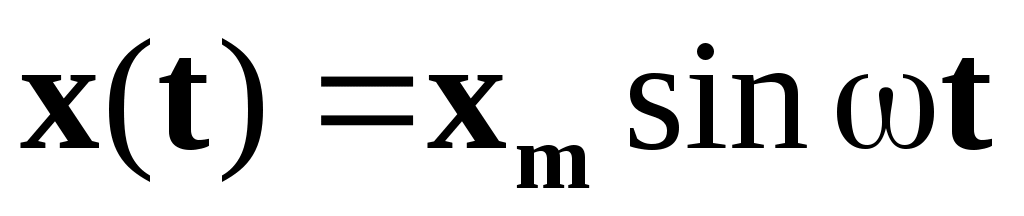 , ,
То на выходе также будут гармонические колебания с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входного сигнала, то есть выходной сигнал изменяется по закону

Где xm, ym – амплитуды входного и выходного сигналов,  - сдвиг фаз между ними. - сдвиг фаз между ними.

y(t)
Преобразующие свойства линейной системы (или звена) определяются характеристиками:
Отношением амплитуды выходного сигнала к амплитуде входного сигнала 
Сдвигом фаз  между выходным и входным сигналами. между выходным и входным сигналами.
Эти величины изменяются с изменением частоты 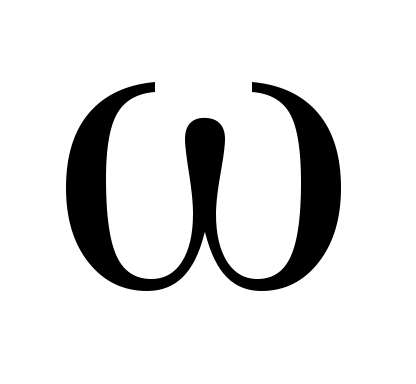 . .
|
АМПЛИТУДНО - ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
|
ЦЕЛИ МОДУЛЯ
1.Общие цели модуля
1.1. Изучить амплитудно-частотные характеристики АПУ и уметь использовать их при проектировании конкретных приборных устройств.
2.Частные цели модуля.
Изучив модуль, Вы сможете:
2.1. Давать определение:
Амплитудно- частотной характеристики;
2.2. Находить выражение:
Амплитудно- частотной характеристики;
|
Амплитудно-частотной характеристикой (АЧХ) называется зависимость от частоты отношения амплитуд выходного и входного сигналов.

А ЧХ показывает, как с изменением частоты ЧХ показывает, как с изменением частоты 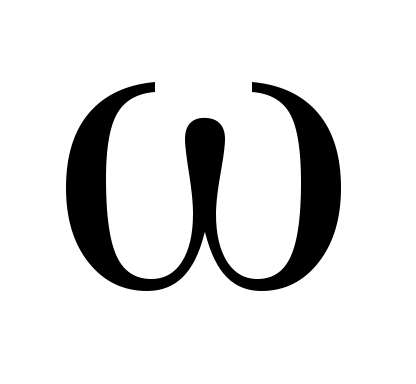 от нуля до бесконечности, изменяется амплитуда выходного сигнала при постоянной амплитуде входного сигнала. от нуля до бесконечности, изменяется амплитуда выходного сигнала при постоянной амплитуде входного сигнала.
|
Методы определения амплитудно-частотных характеристик
Экспериментальный:
На вход системы (звена) подаётся гармонический синусоидальный сигнал постоянной амплитуды  , частота , частота  которого изменяется в заданном диапазоне; которого изменяется в заданном диапазоне;
Для каждой частоты измеряются амплитуды измеряются амплитуды  выходного сигнала. выходного сигнала.
Находят соотношение  ; ;
Изменяя частоту от нуля до наибольшего значения, строят графики - ; ;
|
Аналитический:
Определяют передаточную функцию системы (звена) W(p);
Заменяют в выражении ПФ оператор р на  , ,
получают комплексную амплитудно-фазовую частотную характеристику (комплексный коэффициент передачи) системы (звена)

Где  - вещественная частотная характеристика; - вещественная частотная характеристика;
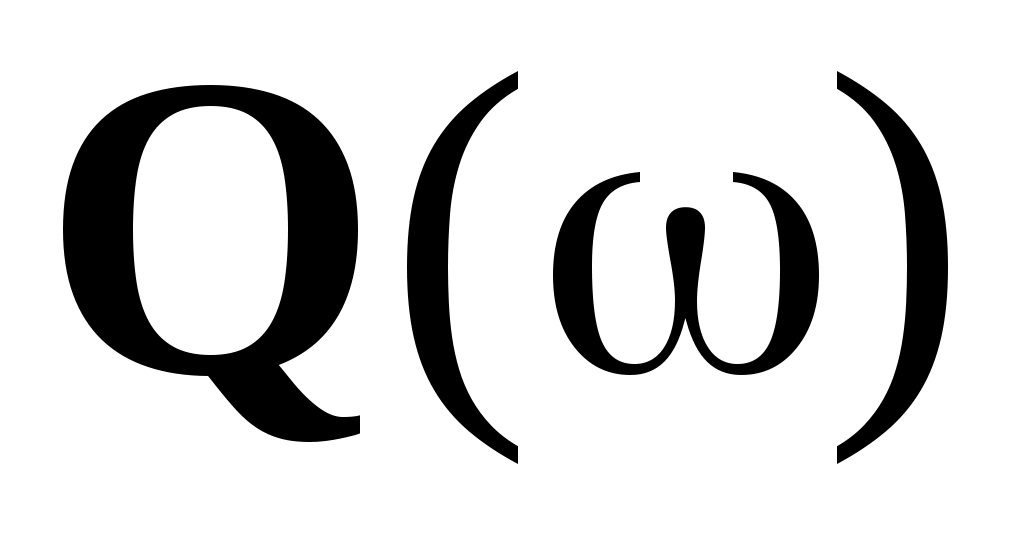 - мнимая частотная характеристика. - мнимая частотная характеристика.
Эти характеристики не имеют физического смысла и не могут быть получены экспериментально, но они используются для определения амплитудно-частотной характеристики 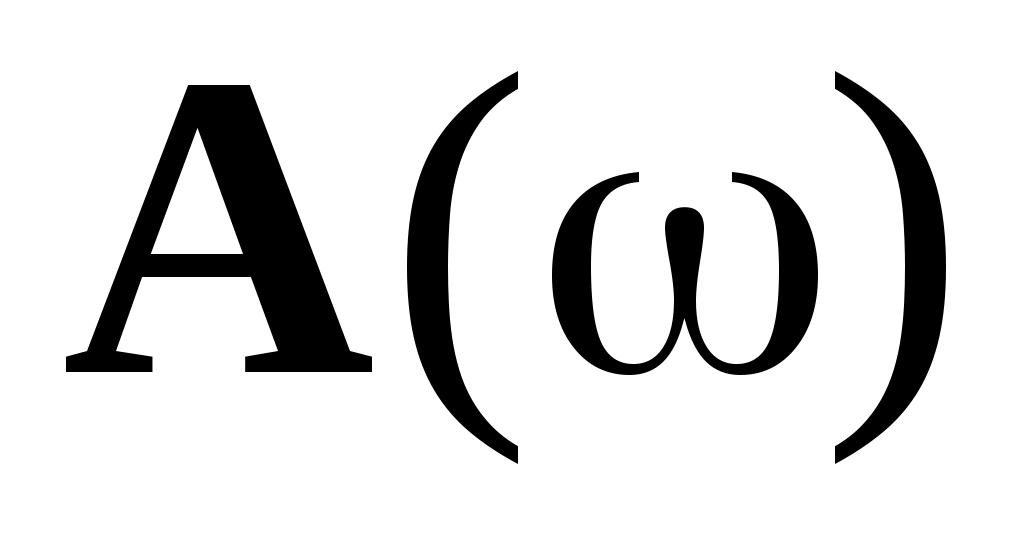 . .
На комплексной плоскости комплексная частотная характеристика  представляется вектором представляется вектором


|
Амплитудно-частотная характеристика:
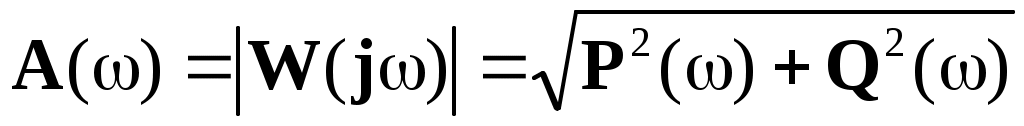
|
|
Тест 1 Вставьте пропущенное слово
АЧХ показывает изменение …………………..выходного сигнала в зависимости от частоты входного сигнала.
Эталон - амплитуда
Подкрепление: изучите модуль «Амплитудно-частотные характеристики»
|
Тест 2. АЧХ является модулем комплексной амплитудно-фазовой частотной характеристики

|
Да
|

|
Нет
|
|
Тест 3. Аналитически АЧХ определяется по выражению передаточной функции

|
Да
|

|
Нет
|
|
ФАЗО - ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
|
ЦЕЛИ МОДУЛЯ
1.Общие цели модуля
1.1. Изучить фазо-частотные характеристики АПУ и уметь использовать их при проектировании конкретных приборных устройств.
2.Частные цели модуля.
Изучив модуль, Вы сможете:
2.1. Давать определение:
фазо- частотной характеристики;
2.2. Находить выражение:
фазо- частотной характеристики;
|
Ф азо-частотной характеристикой (ФЧХ) азо-частотной характеристикой (ФЧХ)  называется зависимость от частоты называется зависимость от частоты 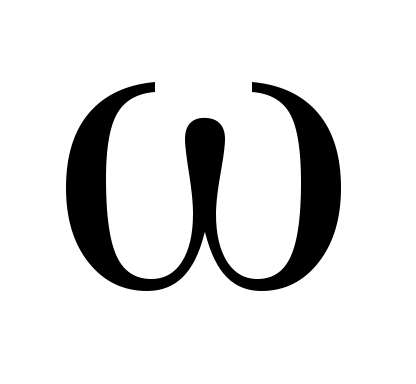 разности фаз входного и выходного сигналов. разности фаз входного и выходного сигналов.
ФЧХ показывает, как с изменением частоты 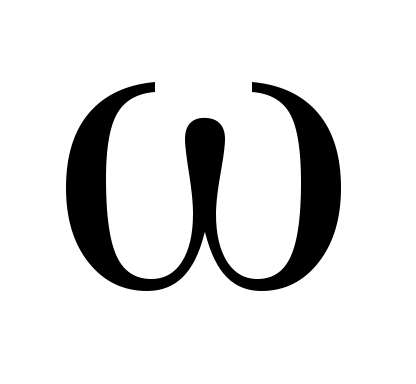 от нуля до бесконечности изменяется сдвиг фаз между входным и выходным гармоническими сигналами. от нуля до бесконечности изменяется сдвиг фаз между входным и выходным гармоническими сигналами.
|
Методы определения фазо-частотных характеристик
Экспериментальный:
На вход системы (звена) подаётся гармонический синусоидальный сигнал, частота  которого изменяется в заданном диапазоне; которого изменяется в заданном диапазоне;
Измеряется для каждой частоты сдвиг фаз сдвиг фаз  между входным и выходным сигналами между входным и выходным сигналами
Изменяя частоту от нуля до наибольшего значения, строят график  ,: ,:
Аналитический:
Определяют передаточную функцию системы (звена) W(p);
Заменяют в выражении ПФ оператор р на  , ,
получают комплексную амплитудно-фазовую частотную характеристику (комплексный коэффициент передачи) системы (звена)

Где  - вещественная частотная характеристика; - вещественная частотная характеристика;
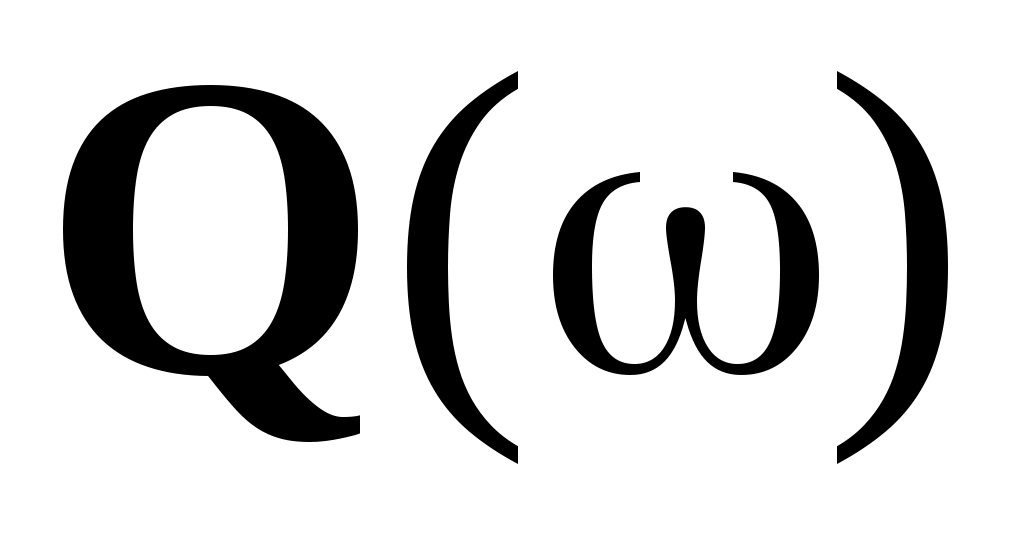 - мнимая частотная характеристика. - мнимая частотная характеристика.
Эти характеристики не имеют физического смысла и не могут быть получены экспериментально, но они используются для определения 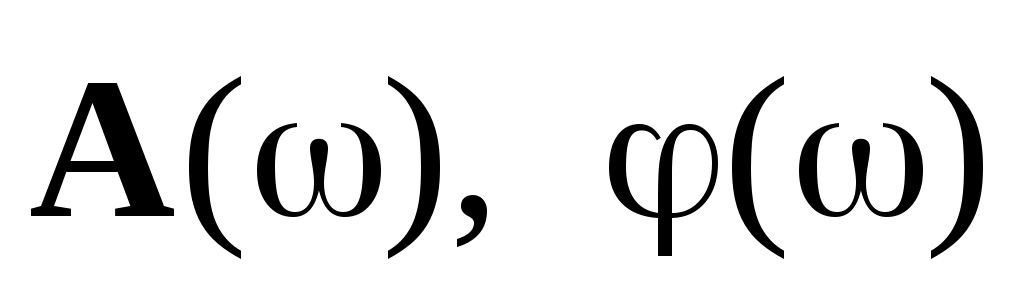 . .
На комплексной плоскости комплексная частотная характеристика  представляется вектором представляется вектором


|
Фазо-частотная характеристика:

|
|
Тест 1 Вставьте пропущенное слово
ФЧХ показывает изменение …………………..выходного сигнала в зависимости от частоты входного сигнала.
Эталон - фаза
Подкрепление: изучите модуль «Фазо-частотные характеристики»
|
Тест 2. ФЧХ является аргументом комплексной амплитудно-фазовой частотной характеристики

|
Да
|

|
Нет
|
|
Тест 3. Аналитически ФЧХ определяется по выражению передаточной функции

|
Да
|

|
Нет
|
|
ЛОГАРИФМИЧЕСКИЕ
АМПЛИТУДНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
|
ЦЕЛИ МОДУЛЯ
1.Общие цели модуля
1.1. Изучить логарифмические частотные характеристики АПУ и уметь использовать их при проектировании конкретных приборных устройств.
2.Частные цели модуля.
Изучив модуль, Вы сможете:
2.1. Давать определение логарифмической частотной характеристики;
2.2. Находить выражения логарифмических частотных характеристик;
|
Логарифмические частотные характеристики (ЛЧХ) используются при исследовании автоматических приборных устройств с помощью частотных методов и представляют собой амплитудную и фазовую частотные характеристики замкнутых или разомкнутых систем (или их элементов), построенные в полулогарифмическом масштабе.
|
Логарифмической амплитудной частотной характеристикой (ЛАЧХ) называется амплитудно-частотная характеристика, построенная в десятичном логарифмическом масштабе частот.

Единица измерения ЛАЧХ – децибел (дБ).
Перевод чисел в децибелы осуществляется по формуле:
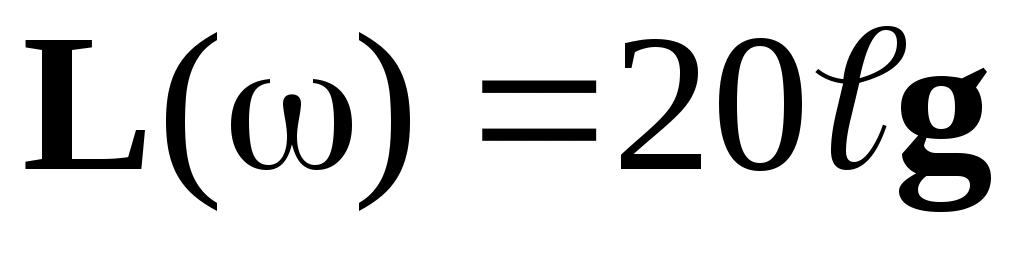 В, В,
Где В – число,  - число В, измеренное в децибелах. - число В, измеренное в децибелах.
20 дБ – соответствует изменению числа в 10 раз.
Декада – соответствует изменению частоты в 10 раз.
  
|
ЛАЧХ имеют наклоны:
20 дБ/дек; 40 дБ/дек; 60 дБ/дек и т. д.
Положительный наклон соответствует увеличению амплитуды выходного сигнала при увеличении частоты.
Отрицательный наклон соответствует уменьшению амплитуды выходного сигнала при увеличении частоты.
Наклоны 20 дБ/дек соответствуют изменению  на 20 дБ (числа В в 10 раз) при изменении частоты на 20 дБ (числа В в 10 раз) при изменении частоты 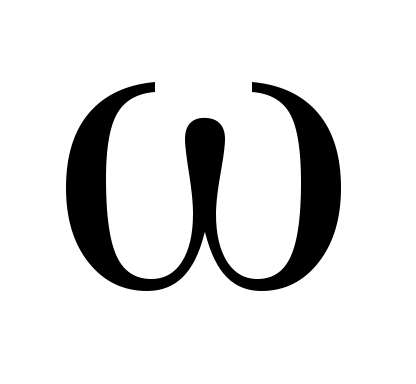 на одну декаду (в 10 раз). на одну декаду (в 10 раз).
Наклоны 40 дБ/дек соответствуют изменению  на 40 дБ (числа В в 100 раз) при изменении частоты на 40 дБ (числа В в 100 раз) при изменении частоты 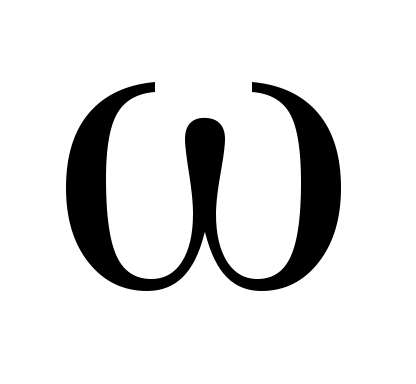 на одну декаду (в 10 раз). на одну декаду (в 10 раз).
Наклоны 60 дБ/дек соответствуют изменению  на 60 дБ на 60 дБ
 (числа В в 1000 раз) при изменении частоты (числа В в 1000 раз) при изменении частоты 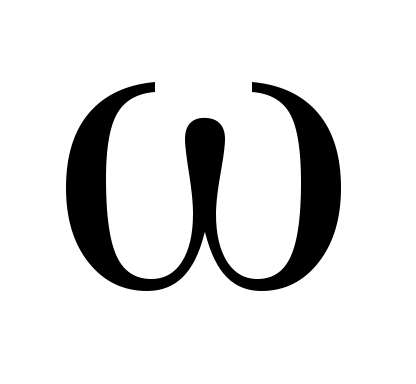 на одну декаду (в 10 раз). на одну декаду (в 10 раз).
С-1
|
Логарифмической фазовой частотной характеристикой (ЛФЧХ) называется фазовая частотная характеристика  , построенная в логарифмическом десятичном масштабе частот. , построенная в логарифмическом десятичном масштабе частот.
По оси ординат значения ЛФЧХ откладываются в градусах (или в радианах)
.


|
Тест 1 Вставьте пропущенное слово
Декада соответствует изменению частоты в ……………раз
Эталон - десять
Подкрепление: изучите модуль «Логарифмические частотные характеристики»
|
Тест 2 Укажите соответствие между коэффициентом «К» и его значением в Дб для характеристики
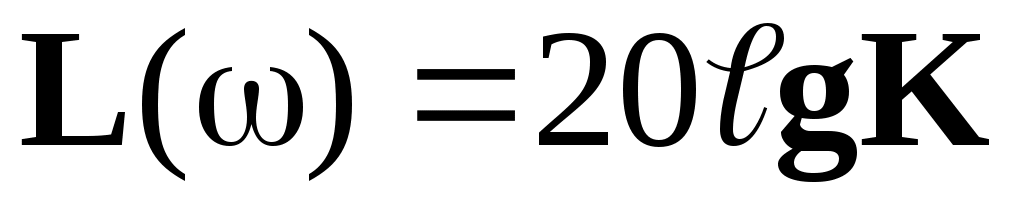

|
20
|
40
|
60
|
80
|
-20
|
-40
|
-60
|
-80
|
0
|
К
|
1
|
0,01
|
0,1
|
100
|
10
|
0,0001
|
10000
|
1000
|
0,001
|
Подкрепление: изучите модуль «Логарифмические частотные характеристики»
|
Тест 3
|

ПОСТРОЕНИЕ
ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
РАЗОМКНУТЫХ ОДНОКОНТУРНЫХ СИСТЕМ
|
ЦЕЛИ МОДУЛЯ
1.Общие цели модуля
1.1. Изучить методику построения ЛЧХ разомкнутой системы и уметь использовать её при проектировании конкретных приборных устройств.
2.Частные цели модуля.
Изучив модуль, Вы сможете:
2.1. Давать определение ЛАЧХ и ФЛЧХ разомкнутой системы
2.2. Применять методику для построения ЛЧХ разомкнутой одноконтурной системы
|
В случае сложных многоконтурных систем предварительно производятся структурные преобразования, приводящие исходную систему к одноконтурной.
Для построения ЛЧХ передаточную функцию системы представляют в виде произведения передаточных функций элементарных динамических звеньев

где - коэффициенты усиления усилительных звеньев; - коэффициенты усиления усилительных звеньев;
Т – постоянные времени элементарных звеньев;
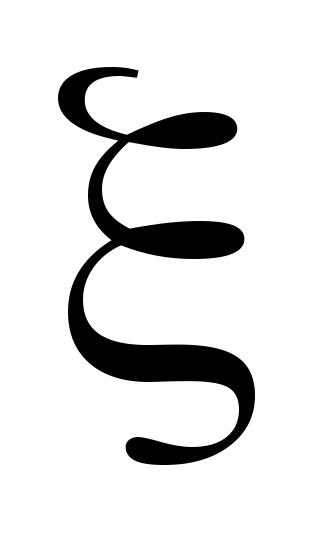 - показатели колебательности звеньев второго порядка; - показатели колебательности звеньев второго порядка;
 - количество интегрирующих (- - количество интегрирующих (- ) или идеально дифференцирующих (+ ) или идеально дифференцирующих (+ ) звеньев (при ) звеньев (при  ) )
Логарифмические амплитудная и фазовая частотные характеристики системы определяются выражениями
 ; ; 
Где n – количество элементарных звеньев;
 и и 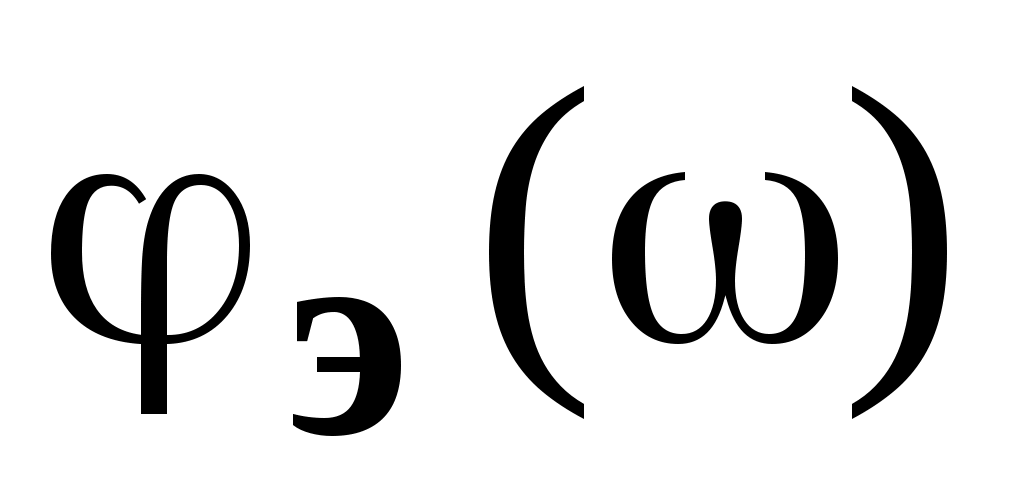 - ЛАЧХ и ФЛЧХ элементарного звена - ЛАЧХ и ФЛЧХ элементарного звена
|
Методика построения ЛАЧХ и ФЛЧХ разомкнутой системы
Записать передаточную функцию разомкнутой одноконтурной системы в виде произведения ПФ элементарных звеньев.
Определить опорные (сопрягающие) частоты звеньев
(   …….; причём …….; причём   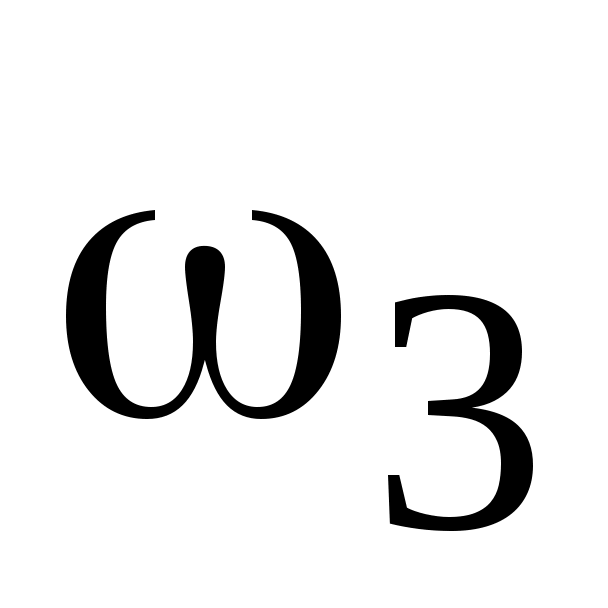 …….). …….).
Отметить опорные частоты на оси абцисс.
Провести низкочастотную асимптоту  : :
если система содержит  интегрирующих звеньев, то асимптота представляет собой при интегрирующих звеньев, то асимптота представляет собой при 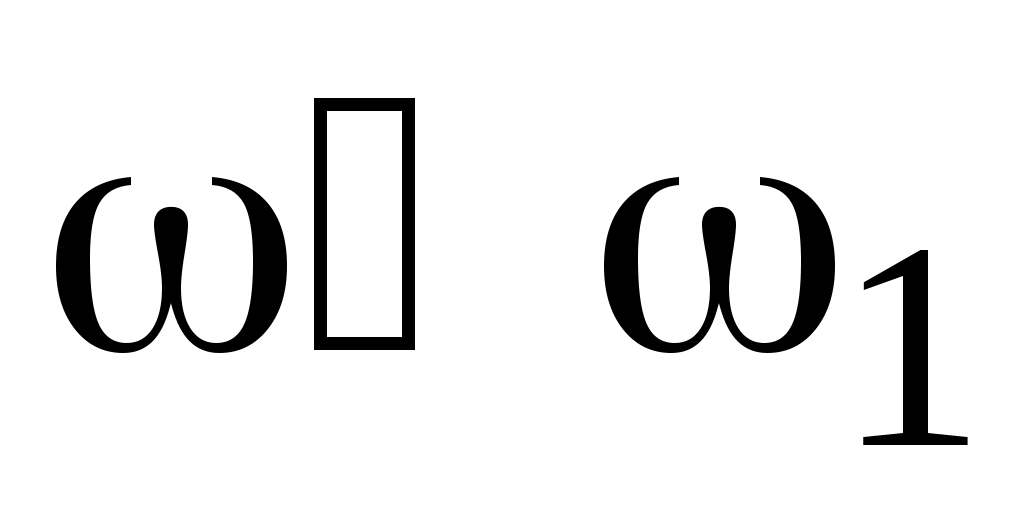 прямую с наклоном прямую с наклоном  , которая пересекает ось абцисс на частоте , которая пересекает ось абцисс на частоте  ; ;
если в системе имеется m идеальных дифференцирующих звеньев, то асимптота представляет собой прямую с наклоном +m, которая пересекает ось абцисс на частоте  ; ;
если система статическая (т.е.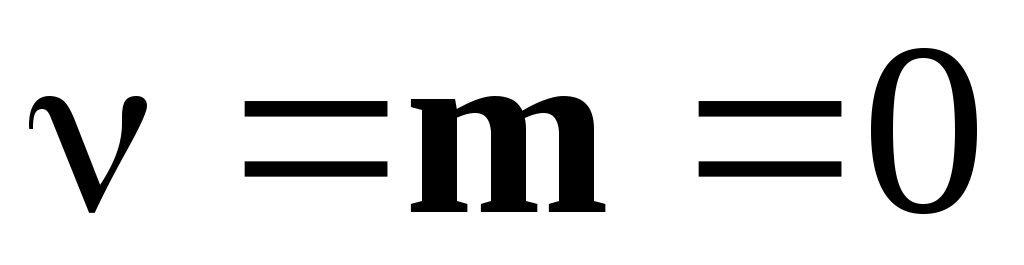 ), то до частоты ), то до частоты 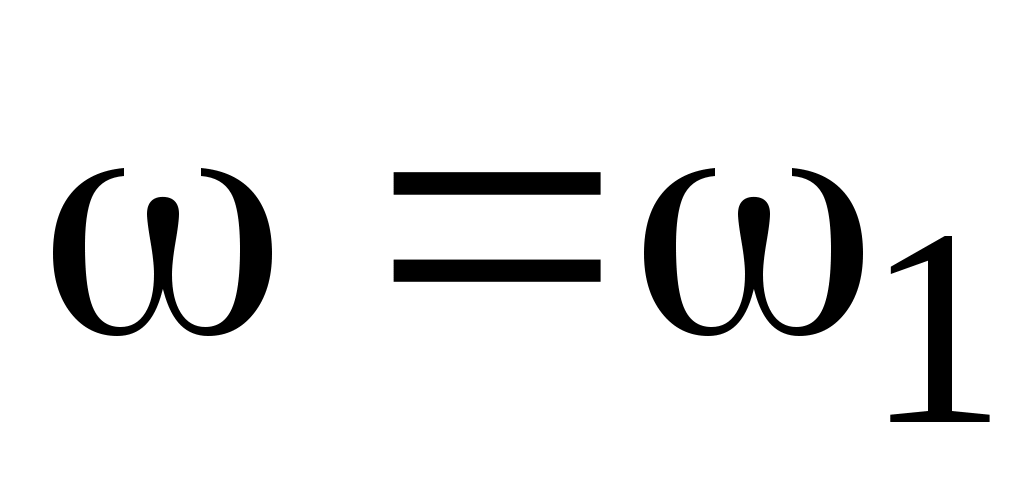 ЛАЧХ будет иметь нулевой наклон к оси абцисс и отстоять от неё на величину ЛАЧХ будет иметь нулевой наклон к оси абцисс и отстоять от неё на величину  . .
Продолжить построение ЛАЧХ, изменяя наклон  после каждой из опорных частот в зависимости от того, какому звену эта частота принадлежит: после каждой из опорных частот в зависимости от того, какому звену эта частота принадлежит:
Каждое апериодическое и дифференцирующее звено первого порядка, начиная с опорной частоты, изменяет наклон ЛАЧХ на -20 или +20 Дб/дек соответственно;
Колебательное и дифференцирующее звено второго порядка даёт изменение наклона на -40 и +40Дб/дек соответственно.
Для колебательного и дифференцирующего звена второго порядка внести поправку на частоте 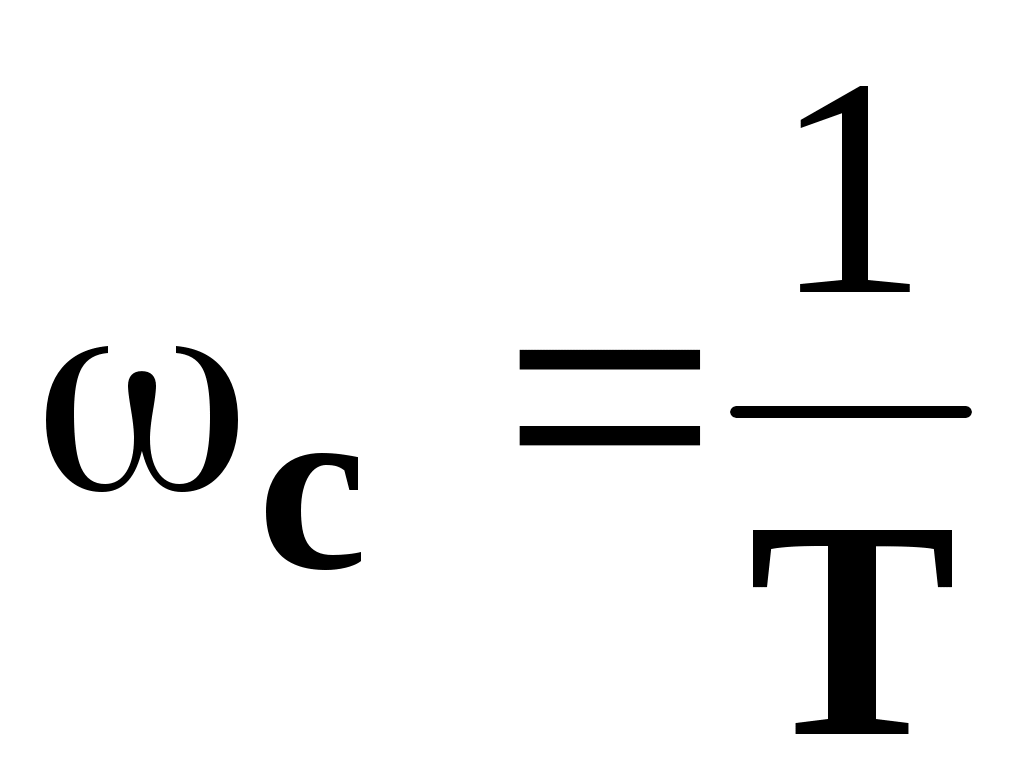 в зависимости от величины коэффициента в зависимости от величины коэффициента 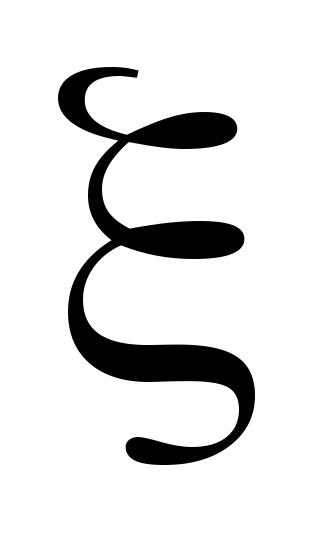 : :
Для колебательного звена  Дб; Дб;
Для дифференцирующего звена  Дб. Дб.
Строятся фазовые частотные характеристики элементарных звеньев системы.
Фазовая частотная характеристика системы определяется как сумма значений ФЧХ каждого из элементов системы на фиксированной частоте.
|
Тест1
|
 Скачать 319.5 Kb.
Скачать 319.5 Kb.