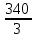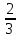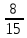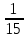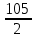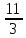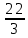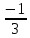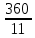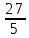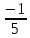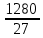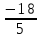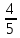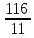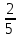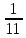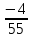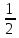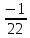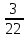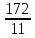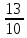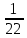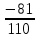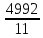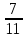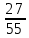Исследование операций. Дослідження операцій. Курсова робота
 Скачать 46.26 Kb. Скачать 46.26 Kb.
|
|
Відкритий міжнародний університет розвитку людини «Україна» Інститут комп’ютерних технологій Кафедра комп’ютерної інженерії КУРСОВА РОБОТА з «Дослідження операцій» (назва навчальної дисципліни) на тему: «___________________________________________________________ ___________________________________________________________» Виконав: студентка ІІІ курсу, групи ЗПІ-18-1 спецiальностi 123 Комп’ютерна iнженерiя (шифр і спеціальнiсть) Барабаш Олени (прізвище ім’я та по батькові) Керівник Тимошенко Оксана Михайлівна (прізвище ім’я та по батькові) Національна шкала: ___________ Оцінка ECTS: ________________ 1.3Знайти максимум і мінімум ф-її і F при умові:   F=3х1 +5х2 мах(min) F=3х1 +5х2 мах(min) x2 ≤10 n=(3;5) 2х1+3х2 ≤ 10 max F=l4∩l5=A( 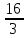 - - 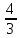 ) ) -х1+4х2 ≤ 9 2х1-х2 ≥ 12 2x2- x2=12 х1+х2 ≤ 4 x1+x2=4 l1 : х2 =10 l2 : 2х1+3х2 ≤=10 х2=4 – х1 х1=0 х2= 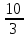 3х1=16 3х1=16х1=5 х2=0 х2= - 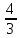 х1 = 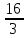 l3 : -х1+4х2=9 х1=0 х2 = 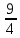 х1=-9 х2=0 min F=R l4: 2х1-х2=12 х1=0 х2=-12 х1=6 х2=0 l5: х1+х2=4 х1=0 х2=4 х1=4 х1=0           2.3
Нехай х1, х2, х3, к-ть прод. А,В, та С відповідно. Складемо математичну модель задачі ; 10х1+15х2 +8х3 ≤ 420 7х1+5х2 +10х3 ≤380 6х1+3х2 +7х3 ≤ 340 Х1, х2, х3 ≥0 10х1 +15х2 +8х3 +х4 =420 7х1+5х2 +10х3 +х5 =380 6х1+ 3х2 + 7х3+ х6=340
Поточний опорний план не оптимальний оскільки в останньому рядку маємо від’ємний коефіцієнт . Визначимо базового змінну х2, оскільки вона має найбільший за моделью коефіцієнт. Min (420; 15; 380; 5; 340; 3)= 28 Отже перший рядок є головним рядком .
Поточний опорний план неоптимальний, ось в останньому рядку маємо від’ємний коефіцієнт. Складаємо нову таблицю:
Серед значень рядка умової ф-її немає від’ємних, тому таблиця визначає оптимальний план задачі. Оптимальний план задачі можна записати так: Х1=0; х2 = 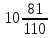 ; х3= ; х3=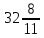 Z(х)= 90+12* 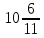 +10* +10*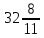 = =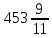 F(x) х; х2 - 3х - 4 = 0; x1 = -1; x2 = 4. y1 = 3; у2 = 8. f(x) = х3 – 5x2 – 32х + 9; б) f(x)=x3 – х2 –3х+5. х1 = 0; х2= 1; х3 = -1. D(f) = [0;+∞). f(х) = (х - 3) -2 < а ≤ 0, f(х) = 2х F1(х) = х2 + 1(х2 + 1)’ = 2х F(x) х; х2 - 3х - 4 = 0; x1 = -1; x2 = 4. y1 = 3; у2 = 8. f(x) = х3 – 5x2 – 32х + 9; б) f(x)=x3 – х2 –3х+5. -[ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||