Угненко курсовая. Курсовая работа бакалавра по направлению 44. 03. 05 Педагогическое образование Профиль Математика и информатика
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
 МИНОБРНАУКИ РОССИИ МИНОБРНАУКИ РОССИИФедеральное государственное автономное образовательное учреждение высшего образования «Южный федеральный университет» Институт математики, механики и компьютерных наук им. И.И. Воровича Кафедра теории и методики математического образования Угненко Анна Александровна Общие вопросы математического моделирования процессов распространения загрязнения окружающей среды КУРСОВАЯ РАБОТА БАКАЛАВРА по направлению 44.03.05 – Педагогическое образование Профиль – Математика и информатика Руководитель – доц., к.ф.м.н. Кузнецова Елена Михайловна Ростов-на-Дону – 2017 СодержаниеВведение 3 1.Математическое моделирование и математическая модель. 5 1.1.Сущность и цели математического моделирования. 5 1.2.Классификация математических моделей 7 1.3.Способы применения математического моделирования в природе 10 2. Математическое моделирование в экологии. 14 2.1. Возможности математической экологии и формы представления эколого-математических моделей. 14 2.2. Основные этапы математического моделирования экологических систем. 16 2.3. Методы математического моделирования при изучении процессов загрязнения окружающей среды 22 2.4. Значение компьютерного математического моделирования в экологии 26 Заключение 28 Список используемой литературы 30 ВведениеВ двадцать первом столетии с каждым годом возрастает актуальность изучения влияния природных и техногенных катастроф на природную среду. Это обусловлено тем, что в результате работы промышленных предприятий и автотранспорта окружающая среда все более насыщается вредными газообразными и конденсированными продуктами (например, оксиды углерода, серы, азота, альдегиды, свинец и др.). Помимо этого, в околоземном слое в процессе фотохимических реакций формируются озон и другие не менее опасные токсиканты как для человеческого здоровья, так и для состояния земной флоры и фауны. При некоторых метеорологических ситуациях даже совсем малые выбросы токсичных веществ веществ могут привести к неблагополучной экологической обстановке в населенных пунктах. Более глобальной опасностью для обитателей Земли являются природные и техногенные катастрофы, теракты, вследствие коих вероятно крупномасштабное загрязнение природы. Например, наиболее яркой демонстрацией данного процесса может служить радиоактивное загрязнения среды по причине аварии на ЧАЭС или промышленной деятельности на Урале, немалые пожары из-за использования ядерного оружия в Хиросиме, горение нефтяных скважин на Ближнем Востоке, массовые лесные пожары в США и в России. Такое пристальное внимание к данному вопросу также обусловлено влиянием крупных очагов горения на приземный атмосферный слой, что всегда вызывает климатические (снижение температуры среды за счет задымленности территорий порождает гибель или более позднее вызревание сельскохозяйственных культур) и экологические последствия. Распространение пожаров на больших территориях может породить такое явление, как «огненный шторм», и в дальнейшем - "ядерная зима". Помимо того, сейчас набирают актуальность проблемы, которые связаны с защитой гидросферы от загрязнения. Аварии, связанные с разливами нефти, и целенаправленные промышленные сбросы отравляющих веществ в водоемы. К примеру, вследствие аварии в Китае была загрязнена река Сунгари –приток российской реки Амур, которая является крупным источником водоснабжения практически всего дальневосточного региона. Актуальность данной работы состоит в том, что изучение вышеуказанных явлений экспериментальным методом является дорогостоящим, а в некоторых случаях и вовсе не представляется возможным проведение полного физического моделирования. По этим причинам наибольший интерес вызывают теоретические методы исследований, наиболее точным и удобным из которых являются методы математического моделирования. В таком случае объектом изучения выступает не сам объект или явление, а его математическая модель. Объект исследования – моделирование в экологии. Предмет исследования – математическое моделирование процессов распространения загрязнения окружающей среды. Цель работы: выявить значимость процессов моделирования в экологии и познакомиться с некоторыми методами моделирования распространения загрязнений окружающей среды. Задачи работы:
Абстрактное построение моделей при помощи математического аппарата является очень мощной познавательной информационной технологией. Процесс изучения математического моделирования дает огромный потенциал для понимания связей математики с естественными и социальными науками. В нынешней математике существует довольно формализованное понимание понятия «математическая модель». Итак, математические модели - широкий класс знаковых моделей, которые основаны на формальных языках конечных алфавитов, обширно применяющих те или иные математические методы. В данном методе в пример моделей можно привести систему целых или действительных чисел, евклидову и неевклидову геометрию, алгебраические группы и т.д[15]. Математическое моделирование в своих разнообразных интерпретациях пользуется практически всем аппаратом нынешней математики:
Математические модели выявляют наиболее важные черты объектов или процессов с помощью языка уравнений и иных средств математики. Вообще говоря, сама математическая наука существует потому, что с помощью нее имеется возможность отразить, т.е. создать модель, на своем особом языке законы окружающего мира. Существенный вклад в развитие математического моделирования внесло создание и развитие ЭВМ, несмотря на то, что сам метод появился в одно время с математической наукой тысячелетия назад. Главное достоинство в использовании компьютерных технологий в моделировании заключается в том, что происходит значительное уменьшение барьера требуемой математической подготовки при построении математической модели. К тому же необходимо отметить, что в настоящее время понятия «аналитическое решение» и «компьютерное решение» совсем не противоречат друг другу, потому что: а) все больше в математическом моделировании применяются компьютеры как для численных расчетов, так и для аналитических преобразований; б) результат аналитических исследований математической модели наиболее часто выражается настолько сложной формулой, что при ее восприятии не формируется образ описываемого ею процесса. Данную формулу требуется протабулировать, изобразить графически, показать описываемый ею процесс в динамике, временами даже озвучить, т.е. визуализировать ее абстракцию. В этот момент компьютер выступает незаменимым удобным техническим средством современного математического моделирования[8]. Главными целями компьютерного математического моделирования выступают: 1) понимание: модель необходима для того, чтобы осознать, каково устройство конкретного объекта, что лежит в основе его структуры, каковы основные свойства, законы развития и взаимодействия с окружающим миром; 2) управление: модель необходима затем, чтобы получить навык управления объектом (или процессом) и найти наиболее удобные и рациональные способы управления при определенных целях и критериях; 3) прогнозирование: модель нужна затем, чтобы получать и строить прямые и косвенные результаты реализации данных методов и форм влияния на объект. 4) разработка концепции управления объектом (например, какой режим полета самолета необходимо предпочесть для того, чтобы полет проходил максимально безопасно и экономически наиболее выгодно?; каким образом построить график выполнения большого количества видов работ при строительстве крупного объекта, чтобы завершить работу в предельно короткий срок?)[5]. Прогноз последствий воздействия на некоторый объект может быть не только довольно легким делом в простых физических системах, но и крайне трудным - на грани выполнимости - в биолого-экономических, социальных системах. Если существует сравнительно легкий ответ на вопрос об модификации режима распространения тепла в тонком стержне при изменениях в сплаве, из которого он состоит, то намного сложнее пронаблюдать и смоделировать экологические и климатические результаты строительства крупной ГЭС или социальные последствия изменения налогового законодательства. Бесспорно, и там математическое моделирование может оказать значительную помощь[1].
В классификации математических моделей можно избрать различные подходы, так как все зависит от принципов, которые закладываются в основу систематизации. Существует возможность классифицировать модели по научным отраслям (математические модели в физике, биологии, социологии и т.д.). Такой способ встречается тогда, когда систематизацию проводит специалист в какой-то одной науке. Можно также классифицировать по математическому аппарату, который был применен (модели, которые основаны на использовании обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.) - это естественно для математика, пользующегося аппаратом математического моделирования. Если человек ставит на первое место цели моделирования и интересуется законами моделирования в разных науках, то можно получить следующую классификацию моделей: • дескриптивные (описательные) модели: строя модель движения кометы, вошедшей в Солнечную систему, можно описать (предсказать) траекторию ее полета, дистанцию, на которой она пройдет от Земли и т. д. , т. е. ставить лишь описательные цели. Не существует ни одной возможности воздействовать на движение кометы, что-то поменять; • оптимизационные модели : если возможно воздействие на объект для того, чтобы добиться некоторой цели, значит в модель можно ввести один или несколько параметров, на которые можно влиять. Например, изменяя тепловой режим в зернохранилище, можно выбрать наиболее оптимальный для того, чтобы получить максимально большой срок сохранности зерна, т. е. оптимизировать процесс; • многокритериальные модели: иногда требуется оптимизация процесса по нескольким параметрам сразу, причем цели могут быть весьма неоднозначными. К примеру, если знать цены на продукцию и потребность человека в пище, то возможна максимально полезная и дешевая организация питания довольно крупных групп людей (в армии, летнем лагере и др.). Совершенно понятно, что такие цели вовсе не совпадают, т.е. в процессе моделирования будет несколько критериев, между которыми необходимо найти баланс; • игровые модели: в игровых моделях может прослеживаться связь не только с детскими играми (в том числе и компьютерным), но и с довольно серьезными вещами. К примеру, полководец в процессе подготовки к сражению в отсутствии полной информации об армии противника обязан разработать стратегию: в какой последовательности вводить в бой те или иные части и т.д. с учетом возможной реакции армии противника. Существует даже особый довольно трудный раздел современной математики - теория игр, - который изучает способы принятия решения в условиях неполной информации; • имитационные модели: бывают ситуации, когда построенная модель сильно схожа с реальными процессами, т.е. имитирует его. Например, при моделировании изменения (динамики) численности микроорганизмов в колонии, есть возможность рассмотреть множество отдельных объектов и проследить за судьбой каждого из них, задавая особые условия для его выживания, размножения и т.д. Притом зачастую явное математическое описание процесса не применяется, а заменяется некоторыми словесными условиями. Например, при моделировании движения молекул в газе, когда каждую молекулу можно представить в виде шарика и задать некоторые условия поведения данных шариков при столкновении друг с другом и со стенками (например, абсолютно упругий удар), причем совершенно не нужно пользоваться никакими уравнениями движений. Таким образом, наиболее часто имитационное моделирование применяют при попытке описания свойства большой системы с условием, что поведение объектов, из которых она состоит, довольно легко и точно сформулировано. Математическое описание тогда возможно произвести на уровне статистической обработки итогов моделирования при нахождении макроскопических характеристик системы. Подобный компьютерный эксперимент направлен на воспроизведение натурного эксперимента. Имитационное моделирование дает возможность выделить «в чистом виде» следствия гипотез, которые были заложены в наших представлениях о микро событиях, которые можно очистить от неминуемого в натурном эксперименте воздействия иных факторов, о которых можно и не задумываться. Если подобное моделирование содержит элементы математического описания событий на микроуровне и при исследовании не ставить задачу нахождения схемы регулирования результатов (например, управления численностью колонии микроорганизмов), то отличий между имитационной моделью и дескриптивной практически нет[9]. 1.3.Способы применения математического моделирования в природеПервые экосистемы, изучаемыми при помощи количественных методов, являются системы «хищник – жертва». А. Лотка из США в 1925 году и В. Вольтерра из Италии в 1926 году построили математические модели изменения численности отдельной популяции, связанной отношениями конкуренции и хищничества. Изучение систем «хищник – жертва» выявило тот факт, что характерная для популяции жертв эволюция - повышение рождаемости, в то время как для популяции хищников – совершенствование и улучшение способов ловли жертв[2]. Со временем метод математического моделирования стал применяться в экологии все больше, что было обусловлено его огромными потенциальными возможностями. Моделирование может дать предварительное объяснение и прогноз поведения экосистемы в условиях, когда теоретический уровень изучения природной среды довольно невысок. В данном случае моделирование постоянно сможет дополнять теоретические построения, потому что разделение практического воздействия на природу и теоретического осмысления последствий данного воздействия остается неизменным, и все качественно новые варианты перестройки биосферы непременно должны быть смоделированы. Модель в качестве средства преобразования можно характеризовать не только соответствием с объектом, который будет преобразовываться. Она строится в соответствии с планирующей деятельностью человека, а значит, с теми орудиями труда, которые имеются в обществе. В модели образуется единство свойств, которые похожи на свойства прототипа и выражают цель, для которой человек ее строит. К примеру, существует возможность использовать в качестве натурной модели при изучении участка под строительство сооружения участок, где уже было реализовано строительство. Итоги модельной деятельности на каждом этапе моделирования сравниваются с результатами использования оригинала с учетом конечной цели преобразования его прототипа. После задания точной цели моделирование могло оправдывать себя до того момента, когда человек не начал преобразовывать огромные территории земного шара. Ведь чем больше территория, тем более разнообразными могут быть способы ее изменения. Потому моделирование разумно применить и для выбора целей изменения большой территории, не забывая его использовать для выбора целей реорганизации биосферы в целом. Особенностью нынешнего периода моделирования является то, что до недавнего времени цели и средства преобразования не зависели от результата моделирования, а сейчас начался учет обратной связи от моделирования к целям и средствам преобразования, и моделирование объекта преобразования начало анализироваться в целостности с моделированием целей и средств преобразования[4]. Осознанный выбор линий изменения природы нуждается в применении разнообразных видов моделирования и типов моделей. Все виды моделирования, которые направлены на постижение природы, применяются в преобразовании биосферы. Использование разнообразных типов моделей и способов моделирования помогает, с одной стороны, росту теоретического статуса науки и синтезу знаний, а с другой, обеспечивает очень нужную в наше время координацию преобразовательной и познавательной стороны деятельности человека. Совершенные модели будущего постоянно складываются в уме человека. И чем больше планы изменений, тем более многогранны эти модели. Подчиненность человека объективным законам развития природы порождает необходимость построения вещественных моделей поведения. В моделировании все модели делятся на две большие группы: модели-интерпретации, которые, главным образом, преобладают в математике, и модели-описания, которые свойственны естественным наукам. В модели в качестве средства преобразования природной среды оба типа моделей используются совместно. Совершенная модель будущего может быть сформирована на основе исследования реальности, но она будет более абстрактно, чем ее прототип. Вещественная модель, которая построена на основе идеальной, будет относиться к моделям-интерпретациям, так как она конкретнее ее прототипа. Масштабная модель нужна тогда, когда нужно установить последствия человеческой деятельности в некотором отрезке времени, чаще всего большем, нежели продолжительность жизни одного поколения. Масштабное моделирование помогает избежать чрезмерного риска при увеличении масштабов действий человечества. Для той же цели используется натурное моделирование в естественных условиях. Оно осуществляется при изучении какого-либо изолированного процесса, но более продуктивно в этом случае комплексное изучение при участии представителей естественных, технических и гуманитарных наук, которое позволит смоделировать также и связи между процессами, которые протекают на данном участке. В этом случае натурная модель может быть применена для оптимизации значительной по масштабу территории[12]. При разработке способов изменения природных систем могут быть применены методы физического, математического и компьютерного моделирования. Для того, чтобы оптимизировать взаимоотношения общества с окружающим природным миром, нужен такой вид моделирования, который мог бы дать возможность учета огромного количества связанных между собой переменных и позволил бы объединить знания из большого количества дисциплин. Причем нужно не только суммировать отдельные процессы, но и учитывать взаимодействие между ними. Реализовать это дает возможность компьютерное моделирование. Оно помогает получить количественный прогноз отдаленных последствий принятия разнообразных альтернативных решений. Изучение поведения модели может помочь найти наиболее эффективные пути достижения оптимального результата на оригинале. Достоинством компьютерного моделирования в сравнении с подлинным экспериментом является его довольно небольшая финансовая затратность и возможность изменения модели при помощи малых усилий. Компьютер дает возможность смоделировать процессы во времени и включить в модель элементы истории системы, что наиболее важно при моделировании необратимых процессов. Переход к компьютерному моделированию возможен на самых ранних стадиях, и в процессе работы результат на «выходе» работы машины показывает, какие эксперименты стоит проводить и как именно нужно изменить модель, чтобы она стала более адекватной прототипу. Если модель как средство познания используют с целью получения прогноза работы какого-либо процесса, то модель в качестве средства преобразования требуется, прежде всего, для управления процессом. Прогноз, используемый в данном случае, носит характер нормативного. Потому подобное моделирование можно назвать нормативным. Информация в компьютерных системах, живых организмах, популяциях и человеческом обществе как воспринимается, так и реорганизуется с формированием на ее основе нормативной модели, которая затем может быть воплощена в действительность. Использование в качестве нормативной математической и других видов моделей значительно увеличивает преобразовательные возможности человека[14]. 2. Математическое моделирование в экологии.2.1. Возможности математической экологии и формы представления эколого-математических моделей.Экология является развивающейся междисциплинарной областью знаний, охватывающая представления почти всех наук о взаимодействиях между живыми организмами, в том числе и человека, с окружающей средой. До середины 20 века экология являлась одной из биологических дисциплин, а именно, наукой о взаимосвязи и взаимодействии организмов с окружающей средой. Нынешняя экология также содержит в себе как теоретическую науку, так и практические методики контролирования состояния окружающей среды: мониторинг, охрана окружающей среды, учение о биогеоценозах, аторопологические воздействия на экосистемы природы, эколого-экономические и экологосоциальные аспекты. Все эти методы определяют предмет математической экологии, которая объединяет математическое моделирование и методы, которые применяются в решениях экологических проблем. Основа математической экологии - математическая теория динамики популяций, формализующая фундаментальные биологические представления об изменениях численности видов животных, растений, микроорганизмов и их взаимодействиях в форме математической структуры, главным образом, систем дифференциальных, интегро-дифференциальных и разностных уравнений. Каждая экосистема представляет собой нелинейно взаимодействующие подсистемы, которые возможно структурировать в некоторые иерархические структуры. В процессе объединения компонентов (подмножеств) в более значительные функциональные единицы в новых единицах появляются свойства, которые отсутствовали в составляющих ее компонентах. Подобные обновленные "эмерджентные" свойства экологического уровня или экологической единицы не являются простой суммой свойств составляющих компонентов. Потому невозможно изучать динамику сложных экосистем с помощью их иерархического разделения на подсистемы и последующего отдельного исследования этих подсистем, так как при этом неминуемо теряются свойства, которые определяются целостностью исследуемой системы. Воздействия сторонних факторов на экосистему также необходимо разбирать одновременно, потому что комбинированное действие невозможно сводить к сумме воздействующих факторов. Потому трудной задачей является количественное описание реакции сложной системы на совместное влияние разнообразных факторов[10]. Все вышеизложенные обстоятельства делают невозможным описание сложных экосистем при помощи простых "механизменных" моделей. Нужны или сложные имитационные модели, которые объединяют в одну сложную систему на уровне модели все знания об элементах системы и способах их взаимодействия, или более простые интегрированные модели типа "воздействие - отклик", которые суммируют данные о большом числе наблюдений над экологической системой. Имитационные компьютерные модели содержат понятия о компонентах систем и их связи как с помощью математических объектов: формул, уравнений, матриц, логических процедур, так и в графическом, табличном виде, в виде базы данных, оперативной информации экологического мониторинга[7]. Подобные многомерные модели дают возможность объединять разрозненную информацию об экологической и эколого-экономической системах, воспроизводить разнообразные сценарии развития и разрабатывать на моделях наилучшие стратегии управления, что невозможно осуществить на реальной системе из-за ее особенностей и временной ограниченности. Имитационный подход, подобно моделированию экосистемы с помощью функций, нуждаются в высокоразвитой вычислительной технике, поэтому математическая экология как сформированная и используемая в практических целях наука приобрела популярность лишь в конце 20 века. В построении математической модели требуется упорядочивание и классификация существующей информации об экосистемах, что вызывает необходимость планирования системы сбора информации и дает возможность объединения на содержательном уровне совокупности физических, химических и биологических знаний и представлений о различных процессах, которые непрерывно происходят в экосистемах. 2.2. Основные этапы математического моделирования экологических систем.Полный процесс моделирования, начинающийся построением моделей и оканчивающийся проверкой предсказанных с ее помощью явлений и внедрением полученных данных в практическую деятельность, всегда связан с точно выработанной стратегией исследования и строгой проверкой данных, которые используются в анализе. Данное положение, являющееся справедливым в математическом моделировании вообще, в особенности значимо для такой сложной науки как экология, исследующей разнообразные взаимодействия между большим множеством организмов и средами их обитания. Практически все взаимодействия являются динамическими, так как зависят от времени и всегда изменяются, причем, обычно содержат в себе положительные и отрицательные обратные связи, то есть являются нелинейными. К тому же, всегда прибавляются совершающиеся независимо изменения таких факторов среды как, например, климатические условия и характер мест обитания, чаще всего вызываемые изменениями экологической обстановки. Потому изучение и регулирование экологических процессов представляет собой исключительно сложную задачу. Экспериментальное и натурное наблюдение экологических процессов усложняется из-за их длительности. По этой причине математическое моделирование можно считать наиболее удобным и необходимым инструментом в экологии, природопользовании и управлении природными ресурсами[4]. Математическое моделирование систем начинают с выбора реальной системы, к которым относят водоемы, лесную экосистему, почвенную экосистему, воздушную среду города и т.п. На выбор системы для моделирования обычно влияют множество причин, как объективных, так и субъективных. Однако решения не всех проблем экологии нужно моделировать. Большое число природоохранных задач возможно решить, не привлекая математики, а основываясь лишь на явных практических действиях в разнообразных экосистемах, промышленности, городском хозяйстве и т.п. Но также имеется огромное число важнейших экологических проблем, которые невозможно решить без заблаговременного построения математической модели. В значительной степени постановка задачи математического моделирования зависит от уровня развития экономики страны и уровня отношения общества к экологическим проблемам. Основными этапами математического моделирования экосистем являются шаги, представленные в следующей схеме: 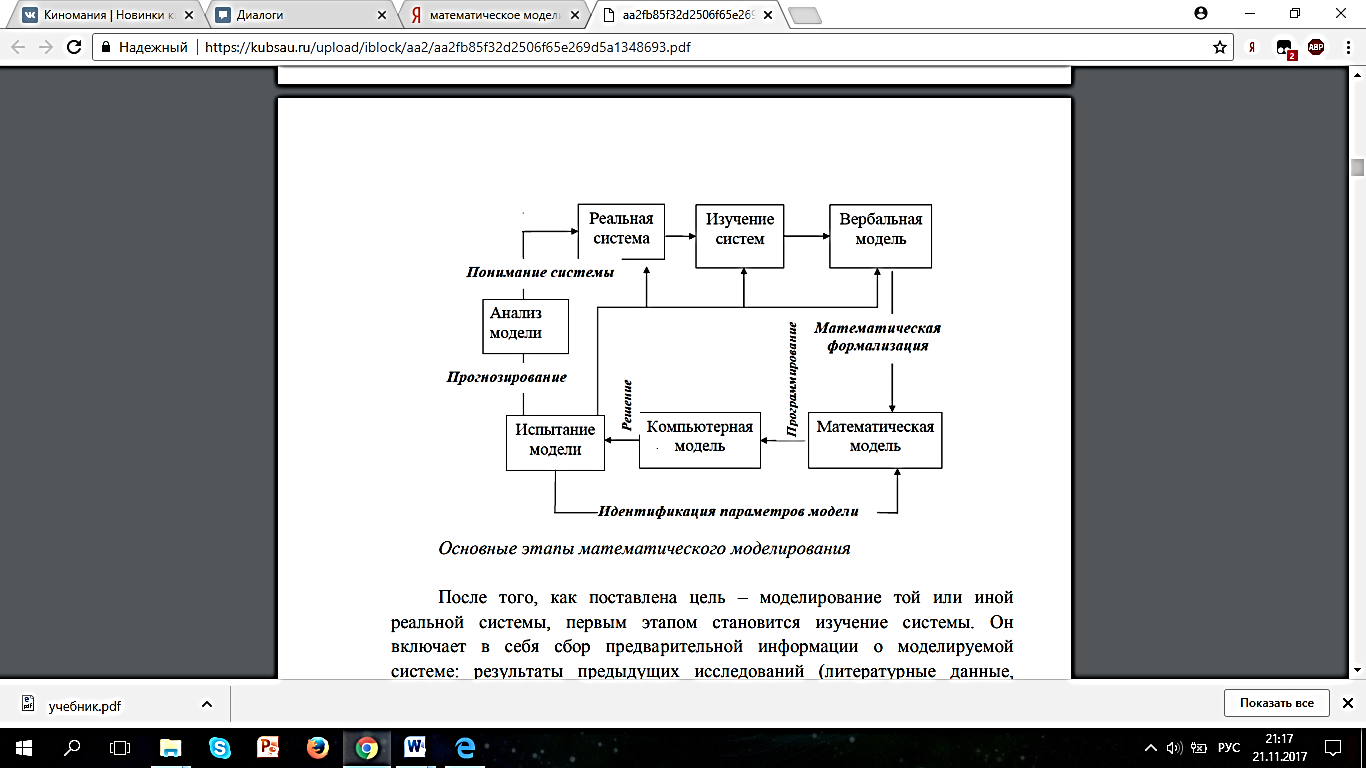 Схема 1. Основные этапы математического моделирования После постановки цели – выбора построения модели той или иной реальной системы, первый этап – это ее изучение. Он содержит в себе сбор предварительной информации о моделируемой системе: результаты предыдущих исследований, постановка собственных экспериментов. Выполнение первого этапа приводит к созданию вербальной модели – словесной модели исследуемой системы (описательный отчет, описательная научная статья). Вербальная модель может давать достаточно полное представление о системе. Многие исследования предметных специалистов – биологов, экологов, химиков ограничены созданием вербальной модели системы. Однако любая словесная модель даже при довольно значительном объеме важной и полезной информации имеет весомое ограничение – она не дает возможность предсказать динамику системы и точно выявить управляющие воздействия на систему с целью оптимизации ее функционирования. Потому для современных наук, в том числе и экологии, следующим важным этапом является создание математической модели системы. Оно начинается математической формализацией – представлением в форме математических переменных количественных характеристик элементов системы (например, концентрация загрязнений, скорость распространения загрязняющего вещества в водоеме, площадь поверхности загрязнения и т.п.). Помимо переменных определяются параметры, описывающие интенсивность разнообразных экологических, биологических, химических и других процессов в экосистеме (коэффициент рождаемости, константа переработки микроорганизмами веществ в минуту, константа скорости химической реакции и т.п.). Данные параметры представляются в форме констант, а также функций времени, пространственных переменных и переменных системы. Математическая формализация и создание математической модели определяется двумя шагами – анализом и синтезом. Анализ системы представляет собой разложение системы исследования на подсистемы и элементы, выявление связей между элементами и процессами в системе. Синтезом называется формулировка математических уравнений на основе выражения связей переменных системы из законов сохранения и гипотез. Результатом синтеза является математическая модель. Эколого-математическая модель – уравнение или система уравнений на основе выражения связей переменных через законы сохранения (балансовые соотношения) или гипотез (предположения о функционировании элементов системы). Математические модели в экологии характеризуют комбинацией уравнений, отражающих законы физики о взаимодействии элементов в системе, и математических гипотез о характере зависимости динамики экологических переменных от различных процессов. К примеру, математическая модель процессов в водоеме содержит в себе систему уравнений гидродинамики, используемых при описании движения жидкой среды, уравнения конвективной диффузии с источниковыми членами, которые описывают распространение и физико–химическую трансформацию антропогенных загрязнений, а также уравнения для динамики биотических компонент в водоеме. Уравнения гидродинамики являются системой уравнений в частных производных, отражающих законы сохранения массы, импульса и энергии в единице объема водной среды. Большое количество математических моделей реальных экосистем представляются системой из нескольких уравнений (например, дифференциальных), которые не имеют аналитических методов решения. Поэтому при решении применяются методы вычислительной математики. И далее появляется задача реализации математической модели, то есть создание компьютерной программы для решения уравнений, описывающих систему[2]. Программированием называют реализацию численных методов решения системы уравнений, описывающих систему, с помощью какого– либо языка программирования или стандартного математического пакета. При данном уровне развития вычислительной математики насчитывается огромное число стандартных библиотек программ на различных языках программирования, а также интегрированные математические пакеты (например, Mathematica, MatLab, Marple, MathCad и т.п.). Кроме этого, в нынешнее время довольно популярны специальные программы расчета для различных предметных областей. Например, таковыми являются пакеты решения задач механики жидкости и газа, так называемые CFD (Сomputational Fluid Dynamics – Вычислительная гидродинамика) пакеты (FLUENT, StarCD, CFX и др.). Использование современных программных возможностей значительно облегчает решение задач математического моделирования, в том числе и в исследовании загрязнения окружающей среды[14]. После того, как реализована математическая модель, на первое место выходит вопрос, является ли достоверной реализованная модель. Наступает этап испытания модели – проверка адекватности созданной математической модели. Проверка правильности построения модели начинают оценкой правдоподобия результатов, приобретенных после расчетов по модели. Рассчитанные значения переменных системы обязаны соответствовать условиям физического и математического правдоподобия (границы изменения переменных должны соответствовать физических пределам и т.п.). Ошибки в модели, которые приводят к неправдоподобным результатам, обычно легко устранимы. Но правдоподобие расчетных результатов, безусловно, не является достаточным для того, чтобы можно было утверждать о достоверности модели. Основной способ проверки математической модели - сравнение с результатами других расчетных работ и с данными эксперимента. Реализованная математическая модель можно также протестировать при решении некоторых частных случаев, когда возможна реализация аналитических решений задачи. Общей рекомендацией здесь может быть пожелание сравнивать полученное решение со всеми данными, с какими возможно, ведь каждое сравнение с положительным результатом дает большую уверенность в достоверности модели, а также помогает понять модель и саму моделируемую систему. Зачастую результаты сравнений с экспериментом и с данными других расчетных работ оказываются изначально отрицательными, имеются количественные или даже качественные расхождения. Чтобы выявить причины, нужно критически проанализировать все предыдущие этапы моделирования. Созданная модель может не учитывать каких–то существенных процессов. При первичном формировании модели выделить наиболее важные и несущественные процессы довольно сложно. Критический анализ как раз и является одной из целей математического моделирования[4]. Следующий ключевой момент - достоверность параметров модели. Уравнения модели могут быть пригодны для описания ряда однотипных процессов (например, уравнения химической кинетики). Применение различных значений параметров для описания конкретных процессов делает математическую модель вполне определенной моделью конкретной системы. И выбор правильных значений параметров модели играет крайне важную роль в адекватности модели реальной системы. Значения параметров модели обычно известны из результатов научных исследований конкретных процессов – химических реакций, динамики атмосферы и т.п. Данные значения определяются с разной точностью. Кроме того, параметры могут быть функциями переменных системы (температуры, площади распространения и т.д.), для выражения которых используют аппроксимации, применяемые в определенных пределах изменения. Таким образом, эти параметры могут содержать в себе ошибки, которые существенно влияют на результаты моделирования. К расхождению с экспериментальными данными могут привести ошибочные гипотезы о характере взаимодействия популяций и неправильное написание уравнений, описывающих различные процессы. Источником ошибок модели может являться и выбранный численный алгоритм решения уравнений модели. В зависимости от того, каков тип уравнений и характер изменения переменных системы, выбирают различные численные методы: методы конечных разностей, конечных объемов или конечных элементов. Все численные методы базируются на сеточном разбиении расчетной области. Правильное сеточное разбиение является необходимым условием получения устойчивого численного решения. Итак, все этапы моделирования могут внести в модель неточности и влиять на достоверность результатов. Поэтому при наличии расхождений в расчете и эксперименте необходимо критически отнестись к этим этапам формирования модели и проанализировать их снова. Чаще всего время, потраченное на уточнение математической модели, может значительно превышать время создания первоначальной модели[5]. 2.3. Методы математического моделирования при изучении процессов загрязнения окружающей средыГлавным требованием к математической модели является согласованность полученных результатов численного анализа с данными экспериментальных исследований. Для выполнения этого условия нужно чтобы: - в математической модели выполнялись фундаментальные законы сохранения массы, энергии и импульса; - математическая модель правильно отражала сущность изучаемого явления. Конечно, ни одно явление невозможно абсолютно точно описать с помощью математической модели и поэтому очень важно указать пределы применимости модели, т.е. определить предположения, используемые при получении основной системы уравнений с соответствующими начальными и граничными условиями. При исследовании этих сложных явлений эффективно применение понятий и методов механики сплошных многофазных реагирующих сред. Опыты применения этого подхода показывают, что при описании фундаментальных законов сохранения в основном используют дифференциальные уравнения параболического типа, так как параболические уравнения — один из примеров универсальности математических моделей. С их помощью возможно описание широкого круга процессов абсолютно различной природы (процессы переноса массы, энергии и импульса). Но они применимы и ко многим процессам, которые рассматриваются как детерминированные (движение грунтовых вод, фильтрация газа в пористой среде и т.д.). Универсальность математических моделей — отражение единства окружающего нас мира и способов его описания. Поэтому методы и результаты, разработанные и накопленные при математическом моделировании одних явлений, относительно легко, "по аналогии", могут быть перенесены на широкие классы совсем других процессов [1]. На основе измерения концентраций загрязняющих ингредиентов строятся их функции распределении, которые в дальнейшем используются для оценки вероятности превышения предельно допустимых концентраций, что говорит о целесообразности моделирования процессов распространения примесей вблизи промышленного предприятия. Например, при помощи построения математической модели можно решить задачу о распространении атмосферных примесей от некоторого источника (пример: рисунок 1). 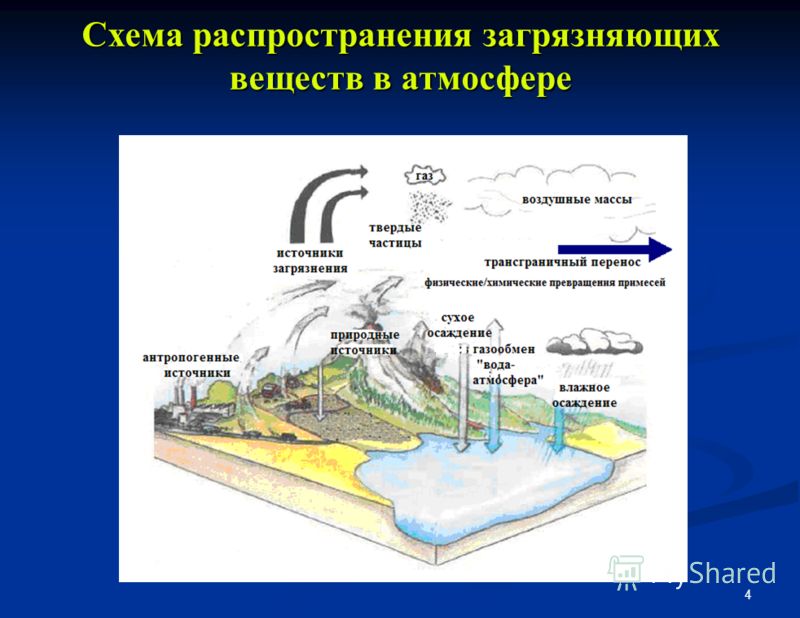 Рисунок 1. Схема распространения загрязняющих веществ в атмосфере Концентрация S загрязняющего ингредиента в рассматриваемой точке зависит от параметров (И) источника, расстояния (d) до него и метеорологических характеристик, определяющей из которых является вектор скорости ветра: Потому можно считать, что величина S зависит от распределения направления ветра. Случайными параметрами считаются ветровые характеристики, наблюдаемые на метеостанциях конкретного региона за многолетний сезон или месяц. Из всего множества ветровых характеристик выбирается только то подмножество, которое влияет на превышение концентрации примесей. Так определяется как область решений дифференциального уравнения, описывающего перенос и турбулентную диффузию примесей, так и область интегрирования заданной функции плотности вероятностей. Интегрируя функцию плотности вектора скорости ветра по выделенному подмножеству, есть возможность оценки с вероятностной точки зрения частоты реализации всех ветров. Несмотря на то, что все аналитические решения получены при определённых упрощениях процессов, возможности их значительно расширяются, если взаимно однозначно связать распределение примесей с вероятностными интегральными и дифференциальными функциями распределения гидрометеорологических параметров. В качестве исходного уравнения получим: где t—время, x,y,z —оси декартовой прямоугольной системы координат, s—концентрация примеси, u,v,w—компоненты вектора скорости ветра, a—коэффициент распада примеси wg—скорость гравитационного осаждения частиц. Можно использовать аналитическое решение, полученное при следующих упрощениях уравнения: лёгкая примесь пассивна и консервативна, движение стационарно, ось х ориентирована в направлении ветра, вертикальные движения в атмосфере малы по сравнению с горизонтальными, диффузионный поток примеси вдоль оси х значительно меньше конвективного[13]. Использование обобщенного уравнения позволяет сформулировать обобщенный численный метод и подготовить многоцелевые программы расчета. В общем случае приходится решать нестационарные пространственные задачи, которые требуют значительных усилий при подготовке программ расчета и достаточно мощной вычислительной техники. Для преодоления вышеуказанных проблем в постановках задач используются обоснованные допущения, не оказывающие значительного влияния на результат расчетов при решении поставленной задачи. Таким образом, с помощью построенной математической модели возможно исследование динамики распространения загрязнения под влиянием различных внешних условий (температуры воздуха, скорости ветра и т.д.), а также параметров источника загрязнения. Сравнивая полученные данные с установленными предельно–допустимыми концентрациями (ПДК) можно проанализировать уровень загрязнения по различным компонентам в различные моменты времени и предложить пути его снижения[11]. 2.4. Значение компьютерного математического моделирования в экологииГоворя об общем значении компьютерного моделирования для решения экологической проблемы, нужно отметить ускорение поиска наиболее приемлемого решения. Человечество получает возможность как бы ускорить свою адаптацию к природе. Руководствуясь в своей деятельности единственным, по существу, методом проб и ошибок (если понимать его в самом широком смысле), человечество вынуждено делать больное количество проб на многих моделях до того, как совершить одну реальную пробу, так как с увеличением технических возможностей значительно возрастает ущерб от ошибки. Компьютерное моделирование вовсе не отменяет прежних способов моделирования, которые широко применимы и на которых строилось и строится планирование человеческой деятельности. Оно дополняет другие виды моделирования по тем параметрам, по которым компьютер превосходит человека: по возможности быстро и логически безупречно просчитать огромное количество вариантов развития системы. В широком применении компьютерного моделирования для решения проблем познания и преобразования природной среды можно видеть соединение двух тенденций, характерных для современной науки, – информатизации и экологизации. Компьютер в настоящее время применяют для выбора оптимальных вариантов использования различных видов ресурсов, для предсказания последствий загрязнения природной среды и т. п. Все большее распространение получают комплексные модели управления экосистемами, вплоть до моделей рационального природопользования в пределах целых регионов. В частности, программа управления системой ресурсов большого водного бассейна принимает во внимание такие факторы, как: - урожай, собранный с орошаемой площади; - количество вырабатываемой электроэнергии; - ущерб, который могли бы причинить паводки и который удалось предупредить сооружением плотин; использование рек и водоемов в целях отдыха и др. Машина моделирует поведение многих переменных, подбирая такую последовательность и комбинацию процессов в системе, которая максимизирует функцию, представленную показателем экономической эффективности многоцелевой системы ресурсов, эксплуатируемых в течение нескольких лет. Намечается тенденция к тому, чтобы строить модели все более комплексные и все больших по размерам регионов. Дело в том, что критерий оптимизации системы каких-либо ресурсов зависит от стратегии использования ресурсов вообще и многих других факторов, связанных с преобразовательной деятельностью человека. Поэтому оптимальный вариант использования данного вида ресурсов может оказаться не оптимальным в рамках более общей задачи. В этой связи наиболее целесообразным выглядит моделирование не только отдельных фрагментов природной среды, но и биосферы в целом, ибо полученные при этом результаты позволяют лучше исследовать модели природных систем, расположенных на более низких структурных уровнях. Поскольку биосфера рассматривается как единое целое, постольку и действия человека по ее познанию и преобразованию (это относится и к моделированию) должны находиться в определенном единстве[6]. ЗаключениеОбщество не может разумно развиваться, не анализируя, контролируя себя, различные стороны своей деятельности, не заглядывая вперед. Но для того чтобы этот анализ был быстрым, он должен опираться на точные, объективные данные, с помощью которых возможно построение модели, ведь моделирование есть один из наиболее эффективных методов исследования, один из путей познания. Совокупность проблем, поддающаяся количественному анализу, может быть выражена языком цифр, то есть, исследована при помощи математического моделирования. При составлении математической модели и решении поставленной задачи применяются методы, в которых вычисления довольно трудоемки. Поэтому для решения данной проблемы и ускорение поиска наиболее приемлемого решения модель строится и обрабатывается на различных компьютерах при помощи математического моделирования. В исследовании проблем экологии и процессов распространения загрязнения окружающей среды также применяются методы математического и компьютерного моделирования, так как с развитием науки все более усложняется химический состав материалов (обработка которых очень токсична), из-за изменения климата высока вероятность возникновения природных и техногенных катастроф, что наиболее сильно может повлиять на экологическую обстановку. Построение эколого-математических и компьютерных моделей использует аналитико-синтетический и экспериментальный методы исследования в зависимости от круга задач, которые ставит перед исследователем выбранная проблема. Многомерные математические модели дают возможность объединять разрозненную информацию об экологической и эколого-биологических системах, воспроизводить разнообразные сценарии развития и разрабатывать на моделях наилучшие стратегии управления, что невозможно осуществить на реальной системе из-за ее особенностей и временной ограниченности. Компьютерная модель в данном случае выступает наиболее удобным помощником, для предсказания последствий загрязнения природной среды, в выборе оптимальных вариантов использования различных видов ресурсов с наименьшим негативным влиянием на существование и развитие экологических систем. . Список используемой литературы
Приложения Приложение 1. Модель распространения примесей от источника в момент времени t=20 при СВ ветре 5 м/с 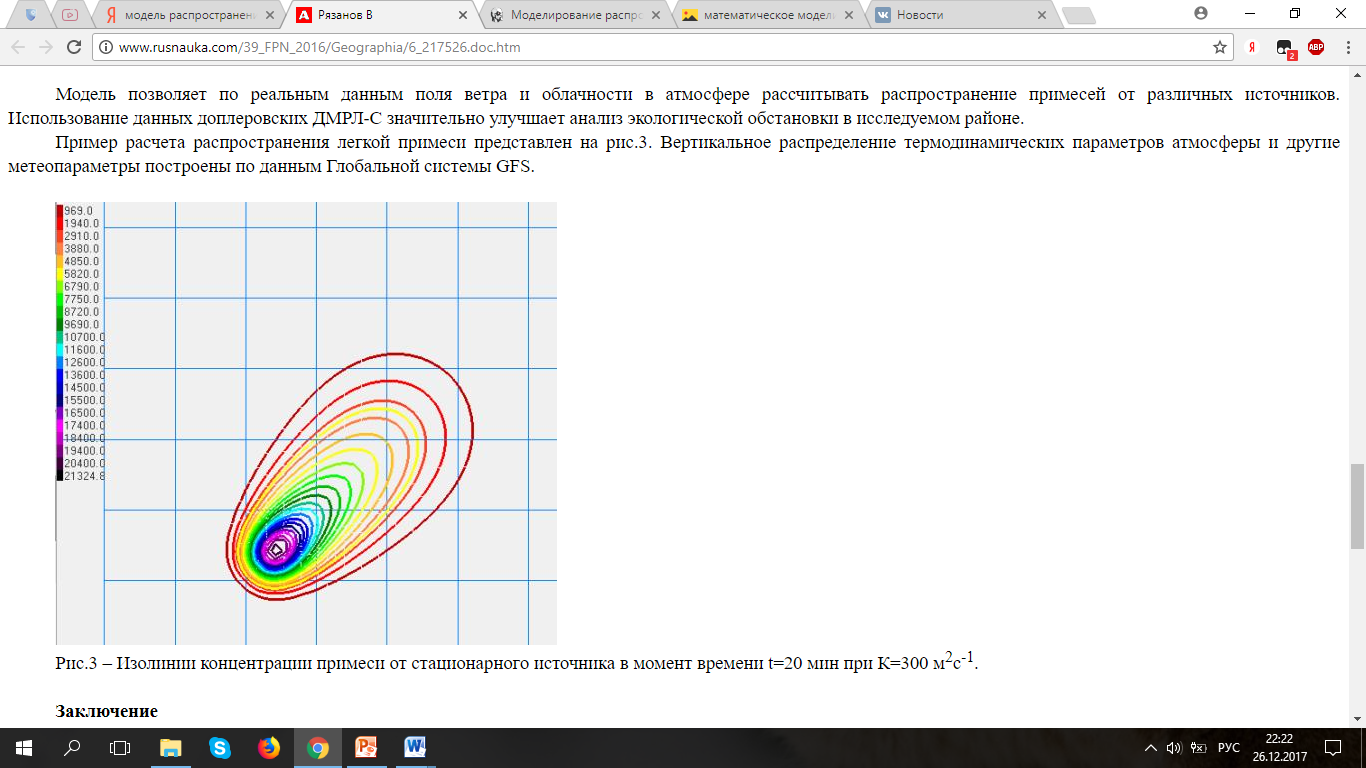 |
