реферат. КР1 В5-1. Курсовая работа часть 1 по дисциплине Информатика
 Скачать 186.5 Kb. Скачать 186.5 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Интернет-институт ТулГУ КУРСОВАЯ РАБОТА ЧАСТЬ 1 по дисциплине «Информатика» Семестр 2 Вариант № 5-1 Выполнил студент: Сибирская Е.В. гр. ИБ360811 интернет института Проверил: канд. тех. наук, доц. Теличко Виктор Григорьевич Тула 2022 Содержание Цель работы 3 Задание 3 1.Описание метода решения 4 2.Программа и ее описание 6 3.Результаты расчета при различных начальных приближениях 7 4.Решение с помощью программы MathCAD 8 4.1.Решение с помощью программы MathCAD 8 4.2.Сравнение результатов расчетов 10 Выводы 11 Список использованных источников 12 Цель работыЦелью работы является закрепление теоретического материала и выработка навыков решения технических задач на примере расчета радиуса выреза для получения заданной емкости конденсатора. ЗаданиеВ интегральных схемах используют планарные конденсаторы, имеющие вид металлического диска, расположенного в круглом вырезе металлизации на поверхности диэлектрической подложки. 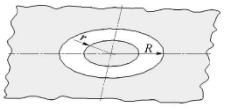 Емкость такого конденсатора определяется по формуле 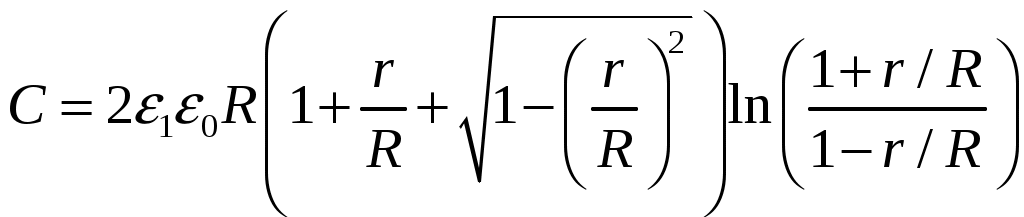 . .где Задавшись указанными в таблице параметрами Данное уравнение является нелинейным относительно 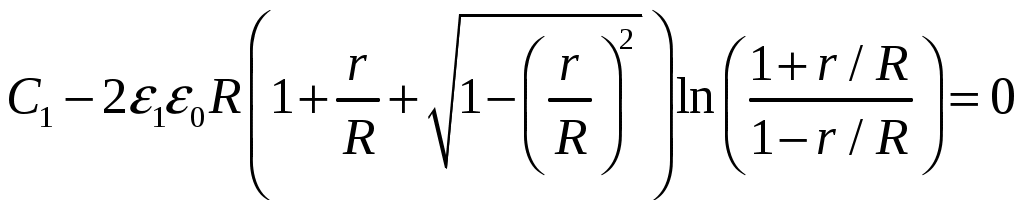 . (1) . (1)Описание метода решенияМетод касательных (метод Ньютона). Пусть на отрезке [a;b] имеется корень уравнения Выбирают начальное приближение корня x0, в качестве которого удобно взять конец отрезка [a;b] для которого Для оценки расстояния очередного приближения хk до корня х* воспользуемся следующими рассуждениями. В соответствии с формулой Лагранжа 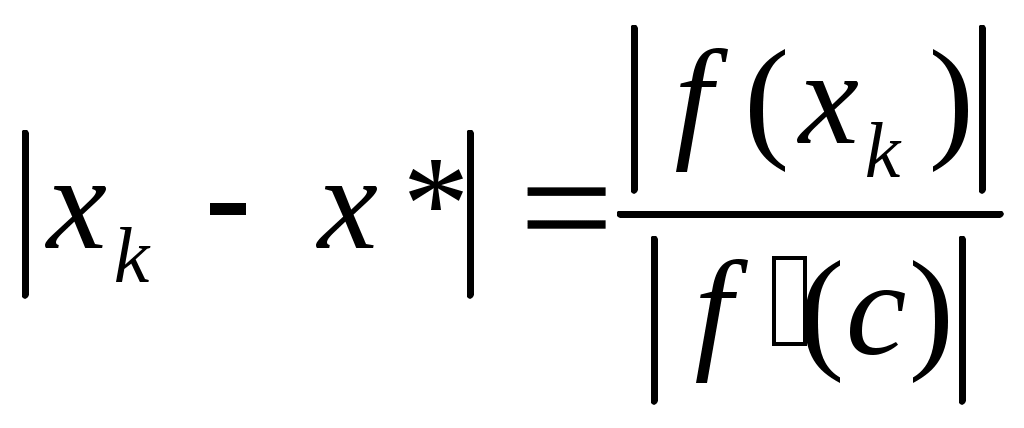 . О точке с известно лишь то, что она находится между хk и х*. Поэтому оценка погрешности возможна с помощью следующего соотношения: . О точке с известно лишь то, что она находится между хk и х*. Поэтому оценка погрешности возможна с помощью следующего соотношения: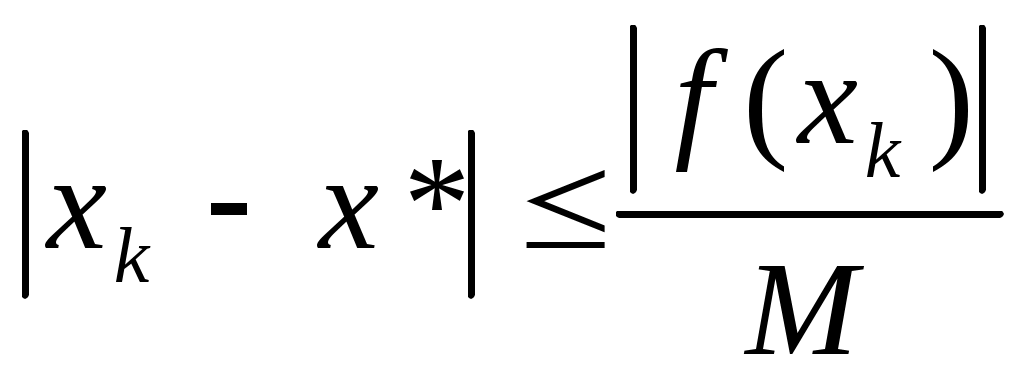 , ,где Метод Ньютона имеет квадратичную сходимость. Иногда, если сложно выбрать начальное приближение, то начинают решение методом деления отрезка пополам (т.е. берут середину отрезка) и продолжают уточнять с помощью метода Ньютона [4]. Метод хорд. При реализации метода касательных, при каждой итерации нужно вычислять значение как функции В качестве с выбирается конец отрезка (точка a или b) для которого выполняется условие Оценка степени приближения к корню производится также, как и при использовании метода касательных [1]. Название методу было дано из-за его геометрического смысла: если Программа и ее описаниеuses Crt; const e0 = 8.85E-12; e1 = 1; C1 = 4.7; r = 0.031; var a, b, aa, bb, x, eps: real; k: integer; function f(x: real): real; begin f := C1-2*e1*e0*x*(1+r/x+Sqrt(1-Sqr(r/x)))* Ln((1+r/x)/(1-r/x))*1E12; end; Begin ClrScr; Write('Введите левую границу отрезка: '); ReadLn(aa); Write('Введите правую границу отрезка: '); ReadLn(bb); WriteLn(); a := aa; b := bb; k := 0; eps := 0.001; {Вычисляем в цикле, пока не достигнуто заданное приближение} repeat k := k + 1; x := a - f(a) * (b - a) / (f(b) - f(a)); if f(a) * f(x) <= 0 then b := x else a := x; until Abs(f(x)) <= eps; WriteLn('Погрешность = ', eps); WriteLn('Число итераций = ', k); WriteLn('Корень уравнения R = ', x:10:8); WriteLn(); a := aa; b := bb; k := 0; eps := 0.000001; {Вычисляем в цикле, пока не достигнуто заданное приближение} repeat k := k + 1; x := a - f(a) * (b - a) / (f(b) - f(a)); if f(a) * f(x) <= 0 then b := x else a := x; until Abs(f(x)) <= eps; WriteLn('Погрешность = ', eps); WriteLn('Число итераций = ', k); WriteLn('Корень уравнения R = ', x:10:8); ReadKey; end. Результаты расчета при различных начальных приближенияхРезультаты расчета приведены на рисунке 1.  Рисунок 1. Решение уравнения с помощью метода хорд Решение с помощью программы MathCADРешение с помощью программы MathCADРешение нелинейного уравнения в системе MathCAD осуществляется функцией root [5, 6]. Синтаксис функции: root(f(х),x,a,b) где f(x) – уравнение, корень которого требуется найти; х - переменная интегрирования; a, b – границы интервала, в котором лежит корень (необязательные параметры). Для решения нелинейного уравнения использовалась конструкция root. Результаты решения нелинейного уравнения (1) с помощью стандартной функции и с помощью метода хорд представлены на рисунках 2-3. Из полученных результатов видно, что значения совпадают с точностью до погрешности.  Рисунок 2. Решение уравнения с помощью встроенной функции  Рисунок 3. Решение уравнения с помощью метода хорд Из полученных результатов видно, что значения совпадают с точностью до погрешности. ВыводыВ данной работе закреплен теоретический материала и выработаны навыки решения и расчета инженерных задач, а также приобретены исследовательские навыки, связанные с решением поставленной задачи. В работе проведено решение нелинейного уравнения стандартной функцией MathCAD и методом хорд. Написана программа, позволяющая решить заданное уравнение методом хорд. Из проведенного тестирования программ видно, что с точностью до погрешности результаты совпадают. Список использованных источниковСамарский А.А., «Введение в численные методы: учебное пособие для вузов.- 3-е изд., стер.», 2009 г., Лань, 288 с. Тыртышников Е.Е., Методы численного анализа: учебное пособие, 2007 г., Академия, 320 с. Махмутов М.М., Лекции по численным методам, 2007 г., РХД, 238 с. Вержбицкий В.М., Основы численных методов, 2009 г., Высшая школа, 848 с. Дьяконов В.П. Mathcad 11/12/13 в математике. -М.: Горяч. Линия-Телеком, 2007. - 958с. Дьяконов В.П. Mathcad 8-12 для студентов. -М.: Солон, 2005. - 632с. Макаров Е. Г. Mathcad. Учебный курс. –СПб.: Питер, 2009. - 384с. Охорзин В.А. Прикладная математика в системе MATHCAD. -М.: Лань, 2008. - 352с. Очков В.Ф. Mathcad 14 для студентов и инженеров: русская версия. -СПб.: BHV, 2009. - 512с. |
