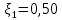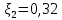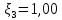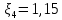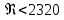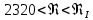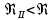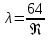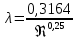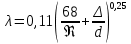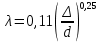Гидравлика. Курсовая. Курсовая работа Гидравлический расчет сложного трубопровода и элементов оборудования по дисциплине Гидравлика и нефтегазовая гидромеханика
 Скачать 195.54 Kb. Скачать 195.54 Kb.
|
|
Министерство высшего образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Кафедра «Гидрогазодинамика трубопроводных систем и гидромашины» КУРСОВАЯ РАБОТА «Гидравлический расчет сложного трубопровода и элементов оборудования» по дисциплине «Гидравлика и нефтегазовая гидромеханика» Выполнил: студент гр. БМТ-19-03 _____________ П.А. Багина (подпись, дата) Проверил: _____________ Л.Р. Байкова (подпись, дата) Уфа 2021 СОДЕРЖАНИЕ1 Задача 2.18 5 Замкнутый резервуар с нефтью (ρ = 900 кг/м3) разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а = 1 м. Давление над нефтью в левой части резервуара определяется показанием манометра M = 15 кПа, а в правой - показанием вакуумметра V = 10 кПа. Уровни нефти указаны на эскизе. Найти величину Р и плечо х результирующей силы давления на крышку, закрывающую отверстие в перегородке. 5 5 Рисунок 1 – Схема к задаче 5 Решение: 5 Сила манометрического давления на перегородку приложена в центре тяжести перегородки и направлена слева направо 5 . 5 Сила вакууметрического давления приложена там же и направлена справа налево 5 . 5 Сила гидростатического давления жидкости на плоскую стенку 5 , 5 где – расстояние от свободной поверхности до центра тяжести стенки площадью . 6 Точка приложения – центр давления 6 , 6 где – центральный момент инерции. 6 Сила давления слева 6 . 6 Расстояние от свободной поверхности до центра давления слева 6 . 6 Сила давления справа 6 . 6 Расстояние от свободной поверхности до центра давления справа 6 . 6 Суммарная сила 6 . 6 Рассмотрим схему сил и обозначим 6 , 6 . 6 . 6 7 Рисунок 2 – Схема действия сил 7 Ответ: . 7 2 Задача 3.1 8 Определить величины и направления сил давления воды на плоское и полусферическое днища цилиндрическою сосуда диаметром D = 1 м в трех случаях: y = + D/5, y = - D/5, y = 0. 8 Показать на чертеже горизонтальные и вертикальные составляющие и полные силы давления воды на днища. 8 8 Рисунок 3 – Схема к задаче 8 Решение 8 Площадь вертикальной проекции плоского и полусферического днища 8 м2. 8 Горизонтальная составляющая силы давления 8 , 8 где – избыточное давление в центре тяжести днища. 8 1) м; Па; Н; 8 2) м; Па; Н; 9 3) м; Па; Н. 9 9 9 Рисунок 4 – Схема действия сил 9 Вертикальная составляющая силы давления на полусферическую крышку во всех трех случаях одинакова, так как объем тела давления одинаков и равен 9 м3. 10 Вертикальная составляющая силы давления 10 , 10 Н. 10 Суммарная сила давления: 10 1) Н кН, 10 , ; 10 2) Н кН, 10 , ; 10 3) Н = 2,57 кН, вертикальная сила проходит через центр тяжести полусферы. 10 3 Гидравлический расчет разветвленного трубопровода 10 Выполнить гидравлический расчет разветвленного трубопровода, схема которого прилагается. Определить Pвх, Q1 = Q2, Q3, Q4. 11 СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 24 1 Задача 2.18 Замкнутый резервуар с нефтью (ρ = 900 кг/м3) разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а = 1 м. Давление над нефтью в левой части резервуара определяется показанием манометра M = 15 кПа, а в правой - показанием вакуумметра V = 10 кПа. Уровни нефти указаны на эскизе. Найти величину Р и плечо х результирующей силы давления на крышку, закрывающую отверстие в перегородке. 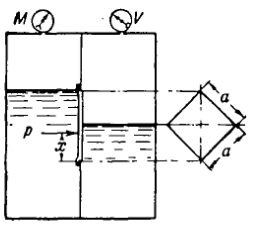 Рисунок 1 – Схема к задаче Решение: Сила манометрического давления на перегородку приложена в центре тяжести перегородки и направлена слева направо 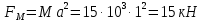 . .Сила вакууметрического давления приложена там же и направлена справа налево 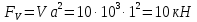 . .Сила гидростатического давления жидкости на плоскую стенку 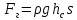 , ,где 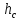 – расстояние от свободной поверхности до центра тяжести стенки площадью – расстояние от свободной поверхности до центра тяжести стенки площадью 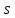 . .Точка приложения 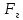 – центр давления – центр давления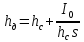 , ,где 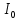 – центральный момент инерции. – центральный момент инерции.Сила давления слева 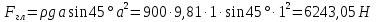 . .Расстояние от свободной поверхности до центра давления слева 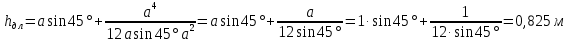 . .Сила давления справа 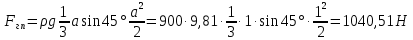 . .Расстояние от свободной поверхности до центра давления справа 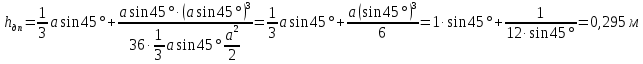 . .Суммарная сила 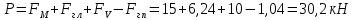 . .Рассмотрим схему сил и обозначим 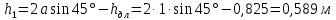 , ,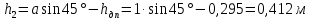 . .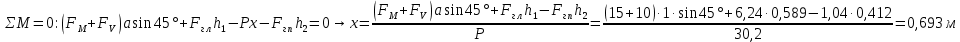 . .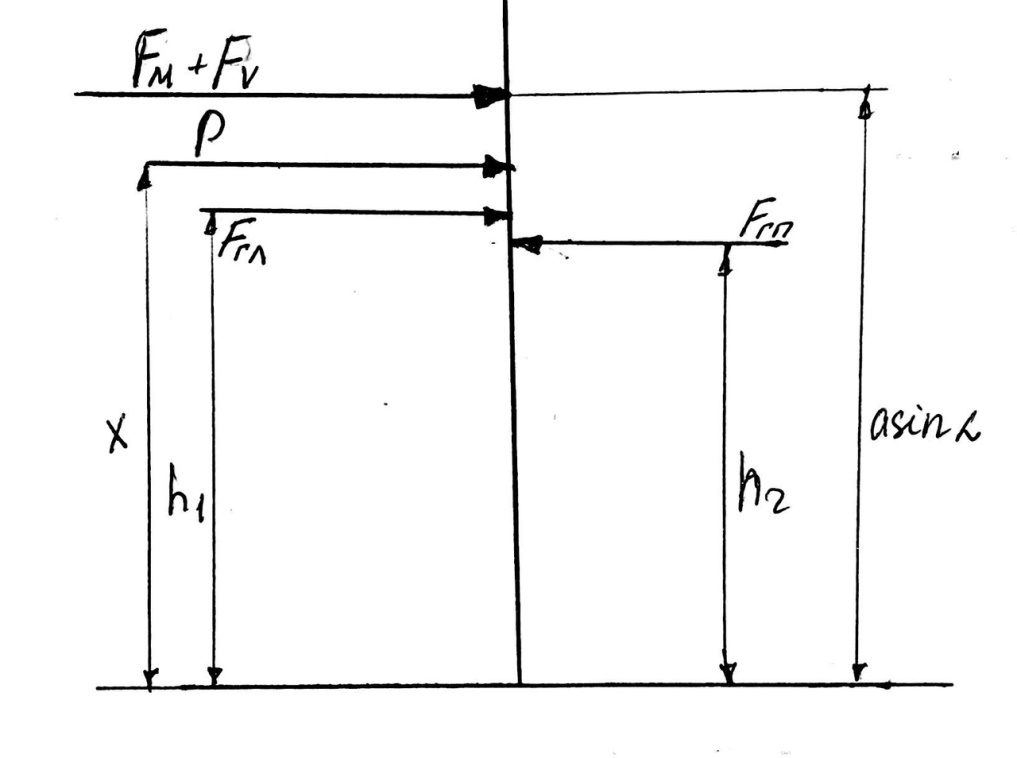 Рисунок 2 – Схема действия сил Ответ: 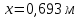 . .2 Задача 3.1 Определить величины и направления сил давления воды на плоское и полусферическое днища цилиндрическою сосуда диаметром D = 1 м в трех случаях: y = + D/5, y = - D/5, y = 0. Показать на чертеже горизонтальные и вертикальные составляющие и полные силы давления воды на днища. 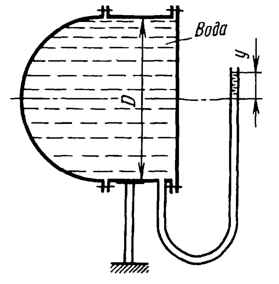 Рисунок 3 – Схема к задаче Решение Площадь вертикальной проекции плоского и полусферического днища 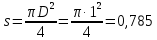 м2. м2.Горизонтальная составляющая силы давления 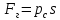 , ,где 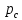 – избыточное давление в центре тяжести днища. – избыточное давление в центре тяжести днища.1) 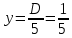 м; м; 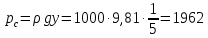 Па; Па; 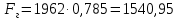 Н; Н;2) 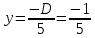 м; м; 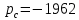 Па; Па; 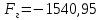 Н; Н;3) 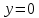 м; м; 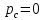 Па; Па; 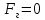 Н. Н.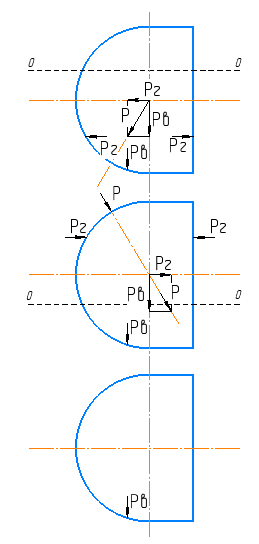 Рисунок 4 – Схема действия сил Вертикальная составляющая силы давления на полусферическую крышку во всех трех случаях одинакова, так как объем тела давления одинаков и равен 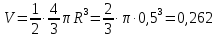 м3. м3.Вертикальная составляющая силы давления 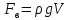 , ,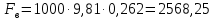 Н. Н.Суммарная сила давления: 1) 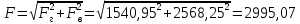 Н Н 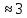 кН, кН,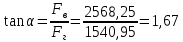 , , 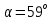 ; ;2) 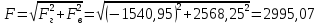 Н Н 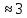 кН, кН,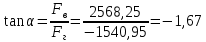 , , 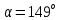 ; ;3) 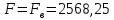 Н = 2,57 кН, вертикальная сила проходит через центр тяжести полусферы. Н = 2,57 кН, вертикальная сила проходит через центр тяжести полусферы.3 Гидравлический расчет разветвленного трубопровода Выполнить гидравлический расчет разветвленного трубопровода, схема которого прилагается. Определить Pвх, Q1 = Q2, Q3, Q4. 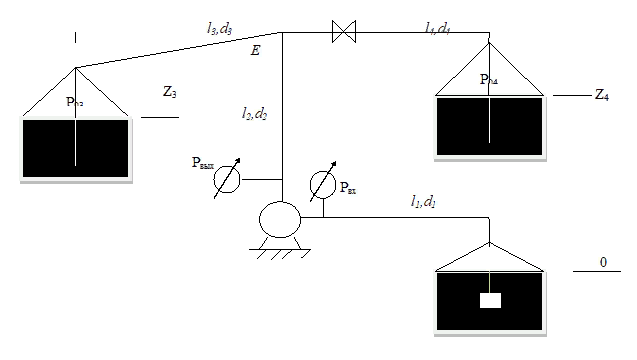 Рисунок 5 – Схема разветвленного трубопровода Исходные данные: Проектный расход, м3/ч _____________ Перекачиваемая жидкость ρ = 900 кг/м3; ν = 30⋅10-6 м2/c Температура перекачки __________________________ Эквивалентная шероховатость_Кэ = 0,2 мм___________
3.1. Теоретическая часть. Для решения сформулированных выше задач составляется система уравнений, устанавливающая связи между размерами труб, расходами жидкости, напорами. Эта система состоит из уравнений баланса расходов для каждого узла и уравнений Бернулли для каждой ветви трубопровода. При этом в сложных трубопроводах можно пренебрегать относительно малыми местными потерями напора в узлах. Это позволяет считать одинаковыми напоры потоков в концевых сечениях труб, примыкающих к данному узлу, и оперировать в уравнениях Бернулли понятием напора в данном узле. Уравнение Бернулли для участка трубопровода 1-2 записывается в виде 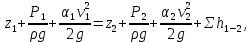 (1) (1)где z – геометрический напор, м; 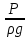 – пьезометрический напор, м; – пьезометрический напор, м;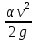 – скоростной напор, м; – скоростной напор, м;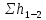 – потери напора, м. – потери напора, м.В данной курсовой работе участки, для которых записываются уравнения Бернулли, на всём протяжении имеют постоянный диаметр, поэтому Потери напора в трубах выражаются формулой Дарси–Вейсбаха (см.[2] стр. 103): 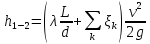 , (2) , (2)где L – длина трубы; d – диаметр трубы; λ – коэффициент сопротивления трения; ξ – коэффициент местного сопротивления; υ – средняя скорость потока в трубе. Поскольку средняя скорость потока в трубе выражается формулой 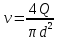 , (3) , (3)где Q – расход жидкости в трубе; то потери напора можно написать в следующем виде 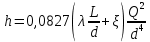 . (4) . (4)Коэффициент гидравлического сопротивления λ зависит от режима течения жидкости и является функцией расхода Q . Так, если режим течения ламинарный 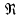 < < 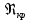 = 2300 и, с учётом того, что = 2300 и, с учётом того, что 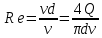 , условие перепишется так , условие перепишется так 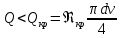 . .Запишем эмпирические формулы для определения коэффициента гидравлического сопротивления λ для каждого режима в таблицу 1. Таблица 1 – Зависимости коэффициента гидравлического от режима течения
где 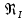 , , 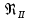 – переходные числа Рейнольдса, определяемые как: – переходные числа Рейнольдса, определяемые как: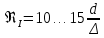 , (5) , (5)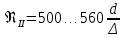 . (6) . (6)Используя тот факт, что 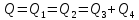 данную задачу можно решить графоаналитическим методом. данную задачу можно решить графоаналитическим методом.3.2. Расчётная часть. Данную схему можно разбить на 4 простых трубопровода, причем трубопровод 1 (l1,d1) является питающим и рассчитывается отдельно от сложного трубопровода, состоящего из трубы 2 (l2,d2), трубы 3 (l3,d3) и трубы 4 (l4,d4), Составим уравнение Бернулли для трубопроводов 1, 2, 3, 4, относительно плоскости отсчета. При этом начальное сечение трубопровода 2 соответствует выходу из насоса, а конечное сечение – в т.E. Для трубопроводов 3 и 4 начальное сечение находится в т.E, а конечное сечение – на входе в резервуары 3 и 4 соответственно. 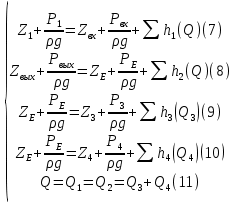 Для решения полученной системы уравнений рассчитаем гидравлические характеристики каждого трубопровода. Так как известен общий расход Q1 в системе, то задаваясь значениями расходов от 0 до 1,2Q, рассчитаем потери напора в каждой из труб по формуле (4). Гидравлическая характеристика трубопровода № 2 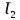 = 200 м ̶ длина трубопровода № 2; = 200 м ̶ длина трубопровода № 2;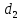 = 0,1 м ̶ диаметр трубы № 2; = 0,1 м ̶ диаметр трубы № 2;ρ = 900 кг/ 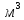 ̶ плотность перекачиваемой жидкости; ̶ плотность перекачиваемой жидкости;ν = 30⋅ 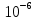 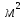 /c ̶ кинематическая вязкость жидкости; /c ̶ кинематическая вязкость жидкости;к = 0,2⋅ 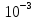 м ̶ эквивалентная шероховатость труб. м ̶ эквивалентная шероховатость труб.Чтобы построить гидравлическую характеристику трубопровода 2, зададимся произвольными значениями скорости от 1 до 5 м/с. Покажем расчет для 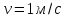 . Определим коэффициент . Определим коэффициент 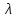 , для этого определим число Re, чтобы определить режим движения жидкости. , для этого определим число Re, чтобы определить режим движения жидкости.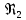 = = 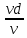 = = 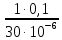 = 3333; = 3333;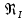 = = 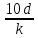 = = 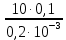 = 5000; = 5000;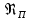 = = 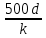 = = 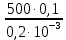 = 250000; = 250000;Т.к. 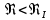 режим движения ̶ турбулентный, зона гладкого трения, и режим движения ̶ турбулентный, зона гладкого трения, и 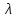 определяется по формуле Блазиуса определяется по формуле Блазиуса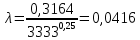 ; ;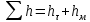 ; ;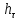 = = 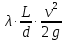 = = 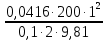 = 4,24 м; = 4,24 м;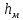 = = 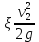 = = 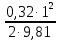 = 0,02 м; = 0,02 м;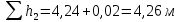 ; ;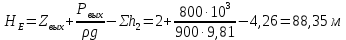 . .Таблица 2 – Данные для построения гидравлической характеристики трубопровода № 2
Аналогично рассчитаем напор в т.Е для трубопроводов 3 и 4, задаваясь различными значениями скоростей от 1 до 5 м/с. Гидравлическая характеристика трубопровода № 3 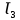 = 150 м ̶ длина трубопровода № 3; = 150 м ̶ длина трубопровода № 3;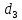 = 0,06 м ̶ диаметр трубы № 3; = 0,06 м ̶ диаметр трубы № 3;ρ = 900 кг/ 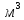 ̶ плотность перекачиваемой жидкости; ̶ плотность перекачиваемой жидкости;ν = 30⋅ 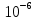 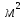 /c ̶ кинематическая вязкость жидкости; /c ̶ кинематическая вязкость жидкости;к = 0,2⋅ 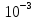 м ̶ эквивалентная шероховатость труб. м ̶ эквивалентная шероховатость труб.Зададимся скоростью в пределах от 1 до 5 м/с и вычислим 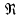 , коэффициент гидравлического сопротивления λ, потери напора ∑ h3 и напор в т.E относительно трубопровода №3. , коэффициент гидравлического сопротивления λ, потери напора ∑ h3 и напор в т.E относительно трубопровода №3.Таблица 3 – Данные для построения гидравлической характеристики трубопровода № 3
Гидравлическая характеристика трубопровода № 4 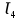 = 130 м ̶ длина трубопровода № 4; = 130 м ̶ длина трубопровода № 4;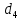 = 0,08 м ̶ диаметр трубы № 4; = 0,08 м ̶ диаметр трубы № 4;ρ = 900 кг/ 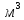 ̶ плотность перекачиваемой жидкости; ̶ плотность перекачиваемой жидкости;ν = 30⋅ 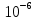 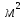 /c ̶ кинематическая вязкость жидкости; /c ̶ кинематическая вязкость жидкости;к = 0,2⋅ 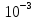 м ̶ эквивалентная шероховатость труб. м ̶ эквивалентная шероховатость труб.Зададимся скоростью в пределах от 1 до 5 м/с и вычислим 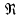 , коэффициент гидравлического сопротивления λ, потери напора ∑ h4 и напор в т.E относительно трубопровода №4. , коэффициент гидравлического сопротивления λ, потери напора ∑ h4 и напор в т.E относительно трубопровода №4.Таблица 4 – Данные для построения гидравлической характеристики трубопровода № 4
Далее решаем полученную выше систему уравнений графоаналитически. Построим график уравнений (8), (9) и (10) в координатах Н-Q. Далее, на основании уравнения (11), сложим графически кривые путем добавления расхода в трубопроводе 3 к расходу в трубопроводе 4 при одинаковом значении напора. Полученная «сиреневая» кривая представляет собой эквивалентную гидравлическую характеристику трубопроводов 3 и 4. Найдем точку пересечения графика гидравлической характеристики трубопровода 2 с графиком эквивалентной гидравлической характеристики трубопроводов 3 и 4 По графику находим значения расходов 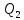 , ,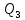 , ,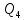 : :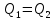 = 93,79 = 93,79 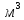 /ч; /ч;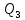 = 28,19 = 28,19 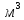 /ч; /ч;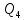 = 65,60 = 65,60 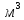 /ч; /ч;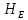 = 55,36 м. = 55,36 м.Гидравлическая характеристика трубопровода № 1 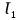 = 50 м ̶ длина трубопровода № 1; = 50 м ̶ длина трубопровода № 1;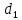 = 0,1 м ̶ диаметр трубы № 1; = 0,1 м ̶ диаметр трубы № 1;ρ = 900 кг/ 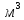 ̶ плотность перекачиваемой жидкости; ̶ плотность перекачиваемой жидкости;ν = 30⋅ 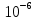 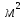 /c ̶ кинематическая вязкость жидкости; /c ̶ кинематическая вязкость жидкости;к = 0,2⋅ 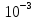 м ̶ эквивалентная шероховатость труб. м ̶ эквивалентная шероховатость труб.Преобразуем уравнение (7), учитывая исходные данные 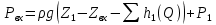 . .Чтобы определить коэффициент 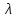 , нужно определить режим движения жидкости , нужно определить режим движения жидкости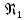 = = 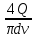 = = 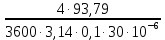 = 11057; = 11057;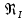 = = 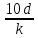 = = 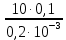 = 5000; = 5000;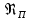 = = 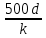 = = 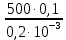 = 250000; = 250000;Т.к. 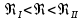 режим движения ̶ турбулентный, зона смешанного трения, и режим движения ̶ турбулентный, зона смешанного трения, и 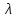 определяется по формуле Альтшуля определяется по формуле Альтшуля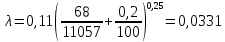 ; ;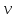 = = 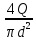 = = 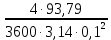 = 3,317 = 3,317 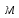 /c; /c;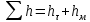 ; ;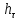 = = 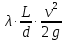 = = 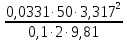 = 9,268 м; = 9,268 м;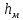 = = 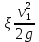 = = 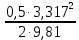 = 0,280 м; = 0,280 м;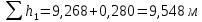 . .Избыточное давление на входе в насос равно 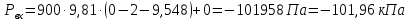 . .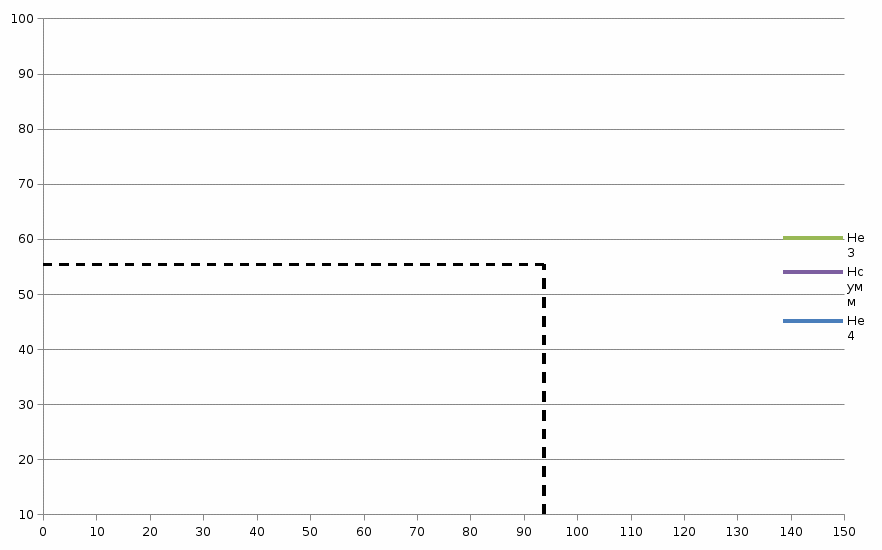 Рисунок 6 – Графическое представление каждого из уравнений системы 3.3 Расчетная часть при изменении вязкости. Проверим зависимость Q1, Q2, Q3, Q4 от вязкости, построив гидравлические характеристики труб, по которым течет жидкость с вязкостью в 0,6 раза больше. Новая вязкость примет значение υ = 18⋅10-6 м2/c. Будем считать, что давление на выходе из насоса осталось прежним. Составим гидравлические характеристики трубопроводов, с учетом зоны трения и расчета коэффициента гидравлических сопротивлений по соответствующим формулам. Таблица 5 – Данные для построения гидравлической характеристики трубопровода №2
Таблица 6 – Данные для построения гидравлической характеристики трубопровода №3
Таблица 7 – Данные для построения гидравлической характеристики трубопровода №4
По графику определяем значения расходов Q1, Q2, Q3 и Q4. Они соответственно равны: 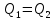 = 98,29 = 98,29 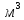 /ч; /ч;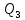 = 29,60 = 29,60 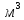 /ч; /ч;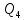 = 68,69 = 68,69 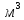 /ч; /ч;Вывод: при изменении вязкости в 0,6 раза (уменьшении), расход увеличивается. 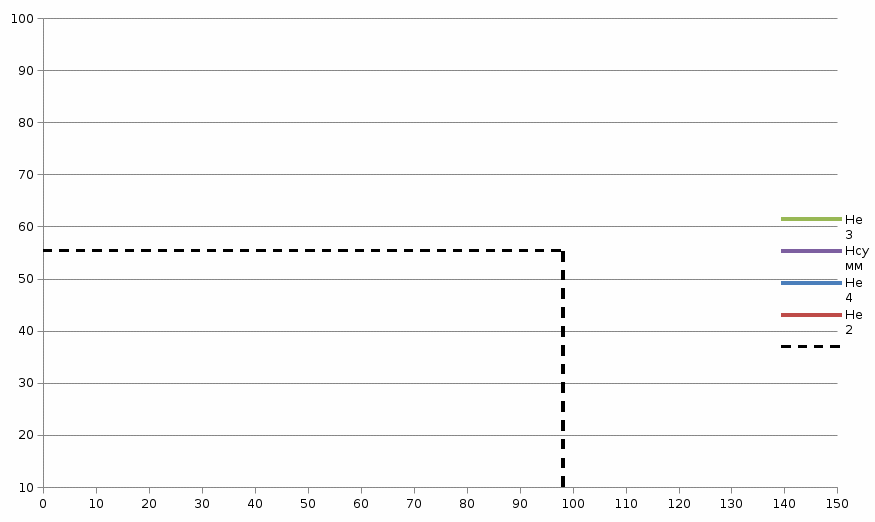 Рисунок 7 – Гидравлические характеристики трубопроводов по которым течет жидкость вязкостью ν = 18⋅10-6 м2/с СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1 Гидромеханика: учеб. пособие по решению задач / Л. Н. Раинкина - М.: Нефть и газ РГУ нефти и газа им. И.М. Губкина, 2005. - 131 с. 2 Прикладные задачи гидравлики: учебное пособие по дисциплинам «Гидравлика» и «Гидромеханика» / Е.Г. Разбегина, А.Р. Сумбатова. – М.: РГУ нефти и газа им.И.М.Губкина, 2007. – 86 с. 3 Учебно-методическое пособие к выполнению курсовой работы по дисциплине «Гидравлика и нефтегазовая гидромеханика» / сост. Л.Р. Байкова, Э.С. Бахтегареева, А.А. Гудникова. – Уфа.: Изд-во УГНТУ, 2014. – 29 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||