Курсовая на тему имитационное моделирование. Курсовая работа Имитационное моделирование Нерюнгри, 2012 Содержание Введение. Имитационное моделирование
 Скачать 5.52 Mb. Скачать 5.52 Mb.
|
3. Технология имитационного моделирования в среде MS ExcelПроведение имитационных экспериментов в среде MS Excel можно осуществить двумя способами - с помощью встроенных функций и путем использования инструмента "Генератор случайных чисел" дополнения "Анализ данных" (Analysis ToolPack). В курсовой работе будет использован первый способ проведения имитационных экспериментов - с помощью встроенных функций MS Excel. Следует отметить, что применение встроенных функций целесообразно лишь в том случае, когда вероятности реализации всех значений случайной величины считаются одинаковыми. Тогда для имитации значений требуемой переменной можно воспользоваться математическими функциями СЛЧИС или СЛУЧМЕЖДУ. Форматы функций приведены в табл. 3. Таблица 3. Математические функции для генерации случайных чисел
Функция "СЛЧИС"Функция СЛЧИС () возвращает равномерно распределенное случайное число E, большее, либо равное 0 и меньшее 1, т. е.: 0 ≤ E < 1. Вместе с тем, путем несложных преобразований, с ее помощью можно получить любое случайное вещественное число. Например, чтобы получить случайное число между a и b, достаточно задать в любой ячейке ЭТ следующую формулу: =СЛЧИС () * (b-a) +a Эта функция не имеет аргументов. Если в ЭТ установлен режим автоматических вычислений, принятый по умолчанию, то возвращаемый функцией результат будет изменяться всякий раз, когда происходит ввод или корректировка данных. В режиме ручных вычислений пересчет всей ЭТ осуществляется только после нажатия клавиши [F9]. Настройка режима управления вычислениями производится установкой соответствующего флажка в подпункте "Вычисления" пункта "Параметры" темы "Сервис" главного меню. В целом применение данной функции при решении задач финансового анализа ограничено рядом специфических приложений. Однако ее удобно использовать в некоторых случаях для генерации значений вероятности событий, а также вещественных чисел. Функция "СЛУЧМЕЖДУ"Как следует из названия этой функции, она позволяет получить случайное число из заданного интервала. При этом тип возвращаемого числа (т. е. вещественное или целое) зависит от типа заданных аргументов. В качестве примера, сгенерируем случайное значение для переменной Q (объем выпуска продукта). Согласно табл. 1., эта переменная принимает значения из диапазона 150 - 300. Введем в любую ячейку ЭТ формулу: =СЛУЧМЕЖДУ (150; 300) (Результат: 210). Если задать аналогичные формулы для переменных P и V, а также формулу для вычисления NPV и скопировать их требуемое число раз, можно получить генеральную совокупность, содержащую различные значения исходных показателей и полученных результатов. После чего, используя статистические функции, нетрудно рассчитать соответствующие параметры распределения и провести вероятностный анализ. Продемонстрируем изложенный подход на решении примера 1. Перед тем, как приступить к разработке шаблона, целесообразно установить в ЭТ режим ручных вычислений. Приступаем к разработке шаблона. С целью упрощения и повышения наглядности анализа выделим для его проведения в рабочей книге MS Excel два листа. Первый лист - "Имитация", предназначен для построения генеральной совокупности (рис. 1.). Определенные в данном листе формулы и собственные имена ячеек приведены в табл. 4. и 5. 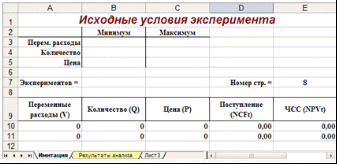 Рис. 1. Лист "Имитация" Таблица 4. Формулы листа "Имитация"
Таблица 5. Имена ячеек листа "Имитация"
Первая часть листа (блок ячеек А1. Е7) предназначена для ввода диапазонов изменений ключевых переменных, значения которых будут генерироваться в процессе проведения эксперимента. В ячейке В7 задается общее число имитаций (экспериментов). Формула, заданная в ячейке Е7, вычисляет номер последней строки выходного блока, в который будут помещены полученные значения. Смысл этой формулы будет раскрыт позже. Вторая часть листа (блок ячеек А9. Е11) предназначена для проведения имитации. Формулы в ячейках А10. С11 генерируют значения для соответствующих переменных с учетом заданных в ячейках В3. С5 диапазонов их изменений. Обратим внимание на то, что при указании нижней и верхней границы изменений используется абсолютная адресация ячеек. Формулы в ячейках D10. E11 вычисляют величину потока платежей и его чистую современную стоимость соответственно. При этом значения постоянных переменных берутся из следующего листа шаблона - "Результаты анализа". Лист "Результаты анализа" кроме значений постоянных переменных содержит также функции, вычисляющие параметры распределения изменяемых (Q, V, P) и результатных (NCF, NPV) переменных и вероятности различных событий. Определенные для данного листа формулы и собственные имена ячеек приведены в табл. 6. и 7. Общий вид листа показан на рис. 2. Таблица 6. Формулы листа "Результаты анализа"
Таблица 7. Имена ячеек листа "Результаты анализа"
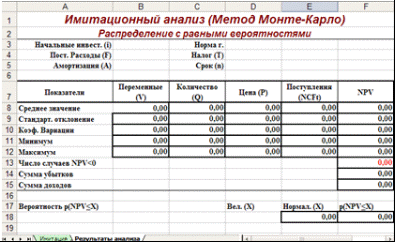 Рис. 2. Лист "Результаты анализа" Поскольку формулы листа содержат ряд новых функций, приведем необходимые пояснения. Функции МИН () и МАКС () вычисляют минимальное и максимальное значение для массива данных из блока ячеек, указанного в качестве их аргумента. Имена и диапазоны этих блоков приведены в табл. 7. Функция СЧЕТЕСЛИ () осуществляет подсчет количества ячеек в указанном блоке, значения которых удовлетворяют заданному условию. Функция имеет следующий формат: =СЧЕТЕСЛИ (блок; "условие"). В данном случае, заданная в ячейке F13, эта функция осуществляет подсчет количества отрицательных значений NPV, содержащихся в блоке ячеек ЧСС (см. табл. 7). Механизм действия функции СУММЕСЛИ () аналогичен функции СЧЕТЕСЛИ (). Отличие заключается лишь в том, что эта функция суммирует значения ячеек в указанном блоке, если они удовлетворяют заданному условию. Функция имеет следующий формат: =СУММЕСЛИ (блок; "условие"). В данном случае, заданные в ячейках F14, F15, функции осуществляет подсчет суммы отрицательных (ячейка F14) и положительных (ячейка F14) значений NPV, содержащихся в блоке ЧСС. Смысл этих расчетов будет объяснен позже. Две последние формулы (ячейки Е18 и F18) предназначены для проведения вероятностного анализа распределения NPV и требуют небольшого теоретического отступления. В рассматриваемом примере мы исходим из предположения о независимости и равномерном распределении ключевых переменных Q, V, P. Однако какое распределение при этом будет иметь результатная величина - показатель NPV, заранее определить нельзя. Одно из возможных решений этой проблемы - попытаться аппроксимировать неизвестное распределение каким-либо известным. При этом в качестве приближения удобнее всего использовать нормальное распределение. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет распределение, приблизительно соответствующее нормальному. В прикладном анализе для целей аппроксимации широко применяется частный случай нормального распределения - т. н. стандартное нормальное распределение. Математическое ожидание стандартно распределенной случайной величины Е равно 0: M (E) = 0. График этого распределения симметричен относительно оси ординат и оно характеризуется всего одним параметром - стандартным отклонением s, равным 1. Приведение случайной переменной E к стандартно распределенной величине Z осуществляется с помощью т.н. нормализации - вычитания средней и последующего деления на стандартное отклонение: Как следует из (2), величина Z выражается в количестве стандартных отклонений. Для вычисления вероятностей по значению нормализованной величины Z используются специальные статистические таблицы. В MS Excel подобные вычисления осуществляются с помощью статистических функций НОРМАЛИЗАЦИЯ () и НОРМСТРАСП (). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
