Курсовая на тему имитационное моделирование. Курсовая работа Имитационное моделирование Нерюнгри, 2012 Содержание Введение. Имитационное моделирование

• Название: Курсовая работа Имитационное моделирование Нерюнгри, 2012 Содержание Введение. Имитационное моделирование
• Анкор: Курсовая на тему имитационное моделирование
• Дата: 05.03.2022
• Размер: 5.52 Mb.
• Имя файла: bibliofond.ru_822722.rtf
• Тип: Курсовая; #383643
• страница: 4 из 5

Функция "НОРМАЛИЗАЦИЯ"

НОРМАЛИЗАЦИЯ (X; СРЕДНЕЕ; СТАНД_ОТКЛ)

Эта функция возвращает нормализованное значение Z величины x, на основании которого затем вычисляется искомая вероятность p (E ≤ x).

Она реализует соотношение (2). Функция требует задания трех аргументов:

х - нормализуемое значение;

среднее - математическое ожидание случайной величины Е;

станд_откл - стандартное отклонение.

Полученное значение Z является аргументом для следующей функции - НОРМСТРАСП ().

Функция "НОРМСТРАСП"

НОРМСТРАСП (Z)

Эта функция возвращает стандартное нормальное распределение, т.е. вероятность того, что случайная нормализованная величина Е будет меньше или равна х. Она имеет всего один аргумент - Z, вычисляемый функцией НОРМАЛИЗАЦИЯ ().

Нетрудно заметить, что эти функции следует использовать в тандеме. При этом наиболее эффективным и компактным способом их задания является указание функции НОРМАЛИЗАЦИЯ () в качестве аргумента функции - НОРМСТРАСП (), т.е.:
=НОРМСТРАСП (НОРМАЛИЗАЦИЯ (x; среднее; станд_откл)).
С целью повышения наглядности, в проектируемом шаблоне функции заданы раздельно (ячейки Е18 и F18).

Приступаем к имитационному эксперименту. Для его проведения необходимо выполнить следующие шаги:

· Ввести значения постоянных переменных (табл. 2.) в ячейки В2, В4 и D2, D4 листа "Результаты анализа".

· Ввести значения диапазонов изменений ключевых переменных (табл. 1.) в ячейки В3, С5 листа "Имитация".

· Задать в ячейке В7 требуемое число экспериментов.

· Установить курсор в ячейку А11 и вставить необходимое число строк в шаблон (номер последней строки будет вычислен в Е7).

· Скопировать формулы блока А10, Е10 требуемое количество раз.

· Перейти к листу "Результаты анализа" и проанализировать полученные результаты.

Рассмотрим реализацию выделенных шагов более подробно. Введем значения постоянных переменных в ячейки В2, В4 листа "Результаты анализа". Введем значения диапазонов изменений ключевых переменных в ячейки В3, С5 листа "Имитация". Укажем в ячейке В7 число проводимых экспериментов, например - 20. Установим табличный курсор в ячейку А11.

На следующем шаге необходимо вставить в шаблон нужное количество строк (18). Теперь необходимо заполнить вставленные строки формулами блока ячеек А10. Е10. Фрагмент результатов имитации приведен на рис. 4. Соответствующие проведенному эксперименту результаты анализа приведены на рис. 5.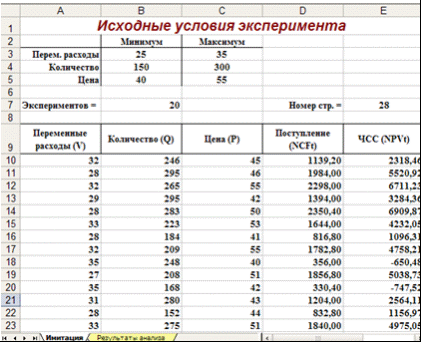


Рис. 4. Результаты имитации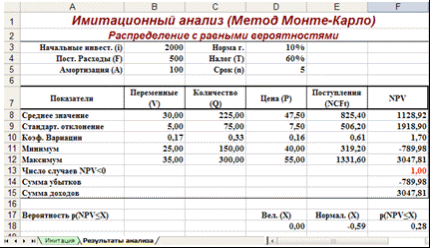


Рис. 5. Результаты анализа
Сумма всех отрицательных значений NPV в полученной генеральной совокупности (ячейка F14) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (ячейка F15) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности проведения дальнейшего анализа.

На практике одним из важнейших этапов анализа результатов имитационного эксперимента является исследование зависимостей между ключевыми параметрами. Количественная оценка вариации напрямую зависит от степени корреляции между случайными величинами. На рис. 6. приведен график распределения значений ключевых параметров V, P и Q, построенный на основании 20 имитаций.

Нетрудно заметить, что в целом, вариация значений всех трех параметров носит случайный характер, что подтверждает принятую ранее гипотезу о их независимости. Для сравнения ниже приведен график распределений потока платежей NCF и величины NPV (рис. 7).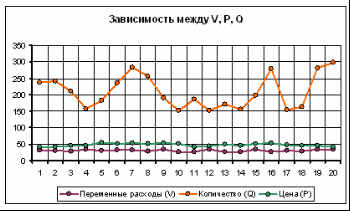


Рис. 6. Распределение значений параметров V, P и Q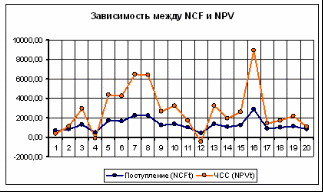


Рис. 7. Зависимость между NCF и NPV

Как и следовало ожидать, направления колебаний здесь в точности совпадают и между этими величинами существует сильная корреляционная связь, близкая к функциональной.

4. Статистический анализ результатов имитации

Как уже отмечалось, в анализе стохастических процессов важное значение имеют статистические взаимосвязи между случайными величинами. В предыдущем примере для установления степени взаимосвязи ключевых и расчетных показателей мы использовали графический анализ. В качестве количественных характеристик подобных взаимосвязей в статистике используют два показателя: ковариацию и корреляцию.