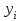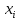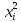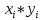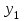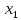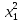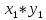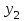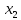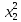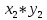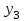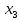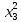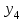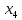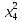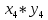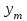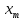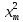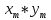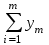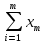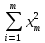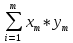Успеваемость студентов. 4. Пояснительная записка. Курсовая работа по дисциплине Алгоритмы и структуры данных
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
1 2 3.5 Базовое правило использования О большого Базовое правило формулируется следующим образом: время выполнения цикла не превышает времени выполнения операторов, входящих в цикл (включая операторы условия), умноженное на число итераций цикла. Время выполнения операторов внутри группы вложенных циклов равно времени выполнения операторов, умноженному на число итераций во всех циклах. Время выполнения последовательности циклов, следующих друг за другом, равно времени выполнения доминантного цикла. Первый случай описывается квадратичной функцией. Второй случай линеен. 3.6 Анализ функции сложности Определение сложности алгоритма сводится к анализу циклов и рекурсивных вызовов. Алгоритмы без циклов и рекурсивных вызовов имеют константную сложность.       T А int i, j, k, t, s, Fin1, Fin2; float* tmp = new float[n]; k = 1;   S while (k < n) {    t = 0; s = 0; t = 0; s = 0;  R B while (t + k < n) {    Fin1 = t + k; Fin1 = t + k;  C Fin2 = (t + 2 * k < n ? t + 2 * k : n); i = t; j = Fin1;  for (; i < Fin1 && j < Fin2; s++) { for (; i < Fin1 && j < Fin2; s++) {   J if (x[i] < x[j]) {   K tmp[s] = x[i];  i++; i++;  E }   L else {     M j++; }   I }   F for (; i < Fin1; i++, s++) {     G }   H for (; j < Fin2; j++, s++) {      N } t = Fin2;   O }   D k *= 2;    P for (s = 0; s < t; s++) {   x[s] = tmp[s];}} x[s] = tmp[s];}}O(J)=O(1)+O(1)=O(1) O(L)=O(1)+O(1)=O(1) O(E)= O(N)*(O(K)+O(M))=O(N) O(R)=O(1)+O(1)+O(1)+O(1)=O(1) O(F)=O(N)*O(1)=O(N) O(G)=O(N)*O(1)=O(N) O(C)=O(N) * (O(R) + O(E) + O(F) + O(G)+O(1))=O(N) * (O(1) + O(N) + O(N) + + O(N) + O(1))= O( 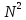 ) )O(D)= O(N) * O(1)=O(N) O(B)= O(N) * (O(1)+O(C) + O(1) + O(D)) = O(N) * (O(1) + O( 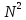 ) + O(1) + O(N))= = O( ) + O(1) + O(N))= = O( ) )O(A) = O(1) + O(B) = O(1) + O(  ) = O( ) = O( ) )Функция сложности алгоритма равна O(  ). ).4 Описание сруктуры программного комплекса На рисунке 3 приведена структура программного комплекса.   Диалоговые окна Интерфейс пользователя      Меню   Ввод-вывод данных  Графическое представление    Бизнес-логика Обработка данных     Оценивание коэффициентов уравнения связи   Расчет коэффициентов корреляции и детерминации    Расчет среднеквадратичной ошибки     Таблицы Хранение данных   Графики Рисунок 3 – Структура программного комплекса. 5 Разработка диаграммы классов На рисунке 4 приведена диаграмма классов.  Form1  button1_Click()    Form2  button3_Click() button4_Click() выходToolStripMenuItem_Click() анализToolStripMenuItem_Click()    Form3  button1_Click() button2_Click() button3_Click() Рисунок 4 – Диаграмма классов 6 Описание структур данных
Таблица 3 – Описание структур данных 7 Описание методики проведения экспериментального исследования 7.1 Математические методы оценивания времени выполнения алгоритмов Цель эксперимента – определение уравнения связи между временем выполнения программного алгоритма (временной параметр T) и размером задачи (емкостной параметр V). В зависимости от постановки задачи разрабатывается регрессионная модель парной корреляции или регрессионная модель множественной корреляции. Например, в случае внешней сортировки данных для установления связи между временем выполнения программного алгоритма и количеством элементов исходного массива разрабатывается классическая регрессионная модель парной корреляции. Пусть оценки коэффициентов являются состоятельными, несмещенными и эффективными. 7.2 Классическая регрессионная модель парной корреляции Классическая регрессионная модель парной корреляции (КРМПК) устанавливает связь между эндогенной переменной и одной экзогенной переменной. Уравнение связи имеет вид  (1)  , ,где 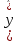 – эндогенная переменная; – эндогенная переменная;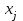 – экзогенная переменная, – экзогенная переменная, 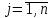 ; ;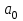 – свободный коэффициент; – свободный коэффициент;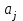 – выборочные коэффициенты; – выборочные коэффициенты;Эндогенная переменная  – время выполнения программного алгоритма решения задачи, экзогенные переменные – время выполнения программного алгоритма решения задачи, экзогенные переменные 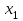 – количество элементов. – количество элементов. Экспериментальное исследование программного алгоритма решения задачи включает этапы: Этап 1. Получение выборки статистических данных в ходе проведения эксперимента на ЭВМ. Количество наблюдений m=10. Результаты проведения эксперимента представляются в таблице 4. Таблица 4 – Исходные статистические данные
Этап 2. Определение уравнения связи в общем виде. По результатам проведения эксперимента на ЭВМ строится и анализируется точечный график зависимости  от от 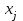 , ,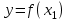 . .Анализ точечного графика позволяет сделать вывод о линейной тенденции. Уравнение связи в общем виде имеет вид (1). где 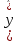 – время выполнения программного алгоритма; – время выполнения программного алгоритма;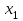 – количество элементов; – количество элементов;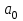 – свободный коэффициент; – свободный коэффициент;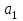 – выборочные коэффициенты. – выборочные коэффициенты.Этап 3. Оценивание коэффициентов уравнения связи. Оценивание коэффициентов 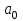 , , 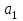 производится МНК (1) по шагам. производится МНК (1) по шагам.Метод наименьших квадратов формулируется следующим образом. Сумма квадратов разности между наблюденной и расчетной эндогенными переменными наименьшая. Уравнение метода наименьших квадратов имеет вид 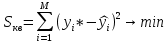 (2) (2)Шаг 1. Подставим в математическое описание (2) МНК вместо 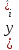 правую часть уравнения связи в общем виде (1). Математическое описание МНК будет иметь вид правую часть уравнения связи в общем виде (1). Математическое описание МНК будет иметь вид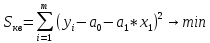 (3) (3)Шаг 2. Определим систему нормальных уравнений для оценивания коэффициентов 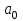 , ,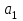 уравнения связи. уравнения связи.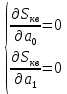 (4) (4)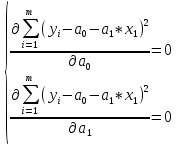 (5) (5) 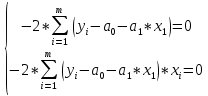 (6) (6)Выполним преобразования: сократим на (-2) левую и правую части, раскроем скобки, сгруппируем слагаемые, заменим аддитивную операцию 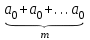 на мультипликативную операцию на мультипликативную операцию 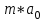 . СНУ имеет вид . СНУ имеет вид (7) (7)Система нормальных уравнений решается методом Гаусса. Этап 4. Анализ уравнения связи и расчет доверительного интервала. Анализ уравнения связи включает расчет линейного коэффициента корреляции, совокупного коэффициента детерминации, частных коэффициентов корреляции, частных коэффициентов детерминации, частных коэффициентов эластичности и частных бэта-коэффициентов. Коэффициент корреляции между  иx рассчитывается по формуле иx рассчитывается по формуле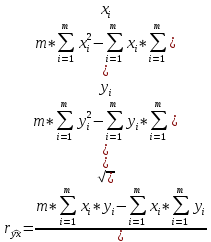 (8) (8)Частные коэффициенты корреляции позволяют провести анализ тесноты связи между эндогенной переменной  и одной из экзогенных переменных при неизменных других. и одной из экзогенных переменных при неизменных других.Коэффициент детерминации рассчитывается как 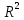 (9) (9) (10) Уравнение регрессии примет вид 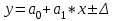 . .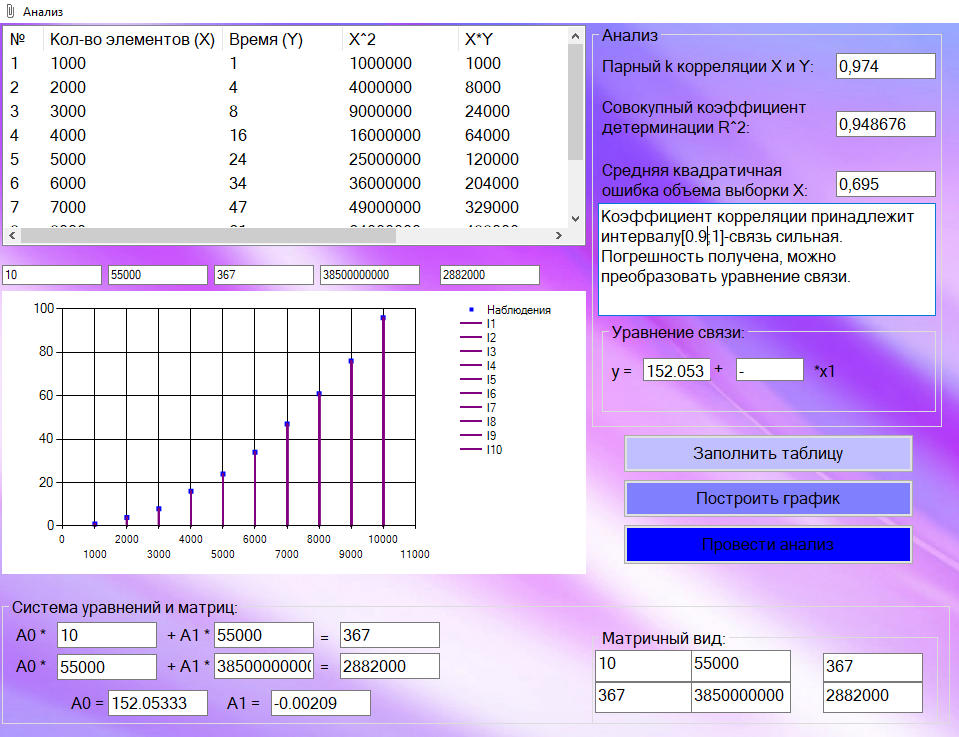 Пример анализа алгоритма приведен на рисунке 5. Пример анализа алгоритма приведен на рисунке 5.Рисунок 5 – Пример анализа алгоритма сортировки методом выбора. 8 Описание и анализ результатов проведенного исследования По результатам проведения экспериментального исследования можно сделать вывод о том, что коэффициент парной корреляции равен 0.974. Это означает, что связь между Y и x переменными – прямая тесная. Коэффициент детерминации 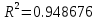 . Это означает, что входная переменная значима и весома. Уравнение связи имеет вид . Это означает, что входная переменная значима и весома. Уравнение связи имеет вид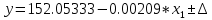 9 Вывод по результатам проведенного исследования В ходе выполнения курсовой работы разработан алгоритм решения задачи. Выполнены: формализация алгоритма метода выбора, оценка сложности программного алгоритма с помощью функции O(n), оценены коэффициенты уравнения связи между временным и емкостным параметрами и анализ уравнения связи. В результате выполнения курсовой работы повышены теоретические знания и приобретены практические навыки в разработке и анализе алгоритмов решения задачи. СПИСОК ЛИТЕРАТУРЫ 1. Ахо Альфред В., Хопкрофт Джон, Ульман Джеффри Д. Структуры данных и алгоритмы: Учебное пособие/Пер. с англ. - М.: Издательский дом «Вильямс», 2000. – 432 с. 2. Каррано Фрэнк М. Абстракция данных и решение задач на С++. Стены и зеркала. – М.; – СПб; – Киев: «Вильямс», 2003г. – 848 с. 3. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы. Анализ и построение. – М.: «БИНОМ», 2000. – 960 с. 4. Сэджвик Р. Фундаментальные алгоритмы на С++. – М.: «DiaSoft», 2001. – 688 с. - Части 1-5. 5. Кубенский А.А. Структуры и алгоритмы обработки данных. Объектно-ориентированный подход и реализация на С++. – Санкт-Петербург: БХВ-Петербург, 2004. - 466 с. 6. Хусаинов Б.С. Структуры и алгоритмы обработки данных. Примеры на языке Си: Учебное пособие. – Финансы и статистика, 2004. – 464 с. 7. Труб И. И. Объектно-ориентированное моделирование на С++: Учебный курс. – СПб.: Питер, 2006. – 411 с. 8.Анашкина Н.В. Технологии и методы программирования: учеб. Пособие для студ. учреждений высш. проф. образования /Н.В. Анашкина, Н.Н. Петухова, В.Ю. Смольянинов. – М.: Издательский центр «Академия», 2012. -384 с. – (сер. Бакалавриат). 9. Павловская Т.А. С/С++. Программирование на языке высокого уровня. – СПб.: Питер, 2006. – 461 с. 10. Павловская Т.А., Щупак Ю.А. С/С++. Структурное программирование: Практикум. – СПб.: Питер, 2007. – 239 с. 11. Давыдов В.Г. Программирование и основы алгоритмизации: Учеб. Пособие. – М.: Высш. шк., 2003. – 447 с. 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||