Успеваемость студентов. 4. Пояснительная записка. Курсовая работа по дисциплине Алгоритмы и структуры данных
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
1 2 Министерство образования и науки Российской федерации федеральное государственное бюджетное образование учреждение высшего образования «Курганский государственный университет» Кафедра «Программное обеспечение автоматизированных систем» РФ КГУ 09.03.04.КР18.701105 02 КУРСОВАЯ РАБОТА по дисциплине «Алгоритмы и структуры данных» Пояснительная записка Листов 28 Курган 2018 АННОТАЦИЯ Проектируемая программная система предназначена для анализа качества алгоритмов сортировки данных, расположенных на внешнем носителе. Основные задачи, решаемые разработчиком в процессе выполнения курсового проекта: Программная реализация алгоритма сортировки данных, расположенных на внешнем носителе. Проведение оценки качества реализованного алгоритма. Программная реализация экспериментального исследования алгоритма и анализ его результатов. Документирование проекта в соответствии с установленными требованиями. Программа состоит из набора программных средств. Программа содержит формы, описывающие программное и информационное обеспечения оптимальной сортировки файлов методом простого слияния. Программный комплекс реализован с использованием языка программирования Microsoft Visual C++. СОДЕРЖАНИЕ Введение…………………………………………………………….......................4 1 Аналитический обзор………….…………………………………......................5 2 Описание алгоритма решения задачи………….….…………………...………6 3 Анализ алгоритма решения задачи…..………….……………………..……....9 3.1 Характеристики алгоритма……………………………………..…….....9 3.2 Функции сложности алгоритмов……………………………..…...…....9 3.3 Виды функций сложности алгоритмов..……….……………....……..11 3.4 Сравнение асимптотического поведения функции…………….…….15 3.5 Базовое правило использования О большого……………………...…17 3.6 Анализ функции сложности……………….………………………......17 4 Описание структуры программного комплекса…..……………....................19 5 Разработка диаграммы классов…………………….…………...……….……20 6 Описание структур данных…...…………………….………….......................21 7 Описание методики проведения экспериментального исследования...........22 7.1 Математические методы оценивания времени выполнения алгоритмов……………………………………………………………………….22 7.2 Классическая регрессионная модель множественной корреляции..22 8 Описание и анализ результатов проведенного исследования……….…...…27 9 Вывод по результатам проведенного исследования……………….………..28 СПИСОК ЛИТЕРАТУРЫ……………………………………………………….29 ВВЕДЕНИЕ Необходимость отсортировать какие-либо величины возникает в программировании довольно часто. Существуют ситуации, когда предварительная сортировка данных позволяет сократить содержательную часть алгоритма в разы, а время его работы – в десятки раз. Данная курсовая работа посвящена рассмотрению одного из важных методов сортировки данных – сортировке файлов методом выбора. Сортировка методом простого выбор является одним из наиболее известных алгоритмов внешних сортировок – сортировок, требующих для работы внешней памяти компьютера. Данные, хранящиеся на внешних устройствах, имеют больший объём, что не позволяет их целиком переместить в оперативную память, отсортировать с использованием одного из алгоритмов внутренней сортировки, а затем вернуть их во внешнее устройство. Для достижения цели необходимо решить следующие задачи: 1 Изучить теоретическое понятие сортировки и алгоритма сортировки. 2 Изучить критерии оценивания алгоритмов сортировок. 3 Изучить описание метода выбора. 4 Разработать собственную программу, реализующую алгоритм сортировки файлов методом выбора. 1 АНАЛИТИЧЕСКИЙ ОБЗОР Данное приложение формализует алгоритм сортировки файлов методом выбора. Программное приложение разработано с использованием технологии визуального проектирование и событийного программирования. Программный алгоритм формализует метод выбора. В программе обеспечен ввод исходных данных, сортировки данных при помощи алгоритма метода выбора и вывод данных в форме таблицы, оценивание коэффициентов уравнения связи между временем выполнения программы и объемом входных данных, анализ коэффициентов уравнения связи. Приложение написано на языке С++ в программной среде Microsoft Visual Studio 2017 Professional. 3 ОПИСАНИЕ АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ Сортировка – один из важнейших аспектов обработки данных, позволяющий ускорить и упростить этот наиважнейший в области вычислительной техники процесс. Под сортировкой в узком смысле контекста вычислительной техники понимают упорядочивание записей внутри структуры данных. Сортировка выбором – возможно, самый простой в реализации алгоритм сортировки. Как и в большинстве других подобных алгоритмов, в его основе лежит операция сравнения. Сравнивая каждый элемент с каждым, и в случае необходимости производя обмен, метод приводит последовательность к необходимому упорядоченному виду. Идея алгоритма очень проста. Пусть имеется массив A размером n, тогда сортировка выбором сводится к следующему: 1. берем первый элемент последовательности A[i], здесь i – номер элемента, для первого i равен 1; 2. находим минимальный (максимальный) элемент последовательности и запоминаем его номер в переменную key; 3. если номер первого элемента и номер найденного элемента не совпадают, т. е. если key≠1, тогда два этих элемента обмениваются значениями, иначе никаких манипуляций не происходит; 4. увеличиваем i на 1 и продолжаем сортировку оставшейся части массива, а именно с элемента с номером 2 по n, так как элемент A[1] уже занимает свою позицию. С каждым последующим шагом размер подмассива, с которым работает алгоритм, уменьшается на 1, но на способ сортировки это не влияет, он одинаков для каждого шага. Пример использования метода выбора приведен на рисунке 1.  Рисунок 1 – Сортировка массива методом выбора. 3 анализ алгоритма решения задач Анализ алгоритма – определение объема ресурсов (памяти и времени выполнения), требуемых алгоритмом для успешной обработки данных. Для оценки качества алгоритма вводятся понятия сложность и эффективность алгоритма. Чем большее время и объем памяти требуются для реализации алгоритма, тем больше сложность и ниже эффективность. 3.1 Характеристики алгоритма Алгоритм обладает набором численных характеристик, сравнивая значения, которых можно произвести выбор наилучшего алгоритма. Сложность алгоритма делится на временную и ёмкостную, практическую и теоретическую. Временная (вычислительная) сложность – критерий, характеризующий временные затраты на реализацию алгоритма. Практическая временная сложность оценивается во временных единицах (миллисекунды, секунды, количество временных тактов процессора, количество выполнения циклов). Емкостная сложность – объем памяти компьютера, требуемый для реализации алгоритма. Практическая ёмкостная сложность выражается в битах, байтах, словах. Вычислительная и емкостная сложности позволяют проводить анализ алгоритмов 3.2 Функции сложности алгоритмов Эффективность программы является важной характеристикой. Пространственная эффективность измеряется количеством памяти, требуемой для выполнения программы. Временная эффективность программы определяется временем, необходимым для выполнения. Сравнение алгоритмов производится сопоставлением порядков сложности. Порядок сложности – это функция, доминирующая над точным выражением временной сложности. Функция 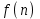 имеет порядок имеет порядок 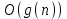 , если имеются константа , если имеются константа  и счетчик и счетчик 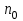 , такие, что выполняются условия , такие, что выполняются условия 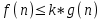 для любых для любых 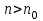 . Например, точное время обработки массива определяется по формуле . Например, точное время обработки массива определяется по формуле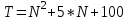 , ,где 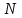 – размер массива. – размер массива.Приближенное время определяется функцией 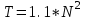 . .Функция сложности – это функция, которая определяет количество сравнений, перестановок, временные и объемные затраты на реализацию алгоритма. Функция сложности О выражает относительную скорость алгоритма в зависимости от переменных. Для функции сложности сформулированы три правила: 1) 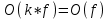 . Постоянные множители не имеют значения для определения порядка сложности, например, . Постоянные множители не имеют значения для определения порядка сложности, например, 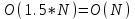 ; ;2) 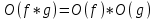 , ,  . Порядок сложности произведения двух функций равен произведению их сложностей, например, . Порядок сложности произведения двух функций равен произведению их сложностей, например, 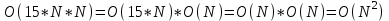 ; ;3) 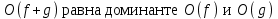 . Порядок сложности суммы функций определяется как порядок доминанты первого и второго слагаемых (выбирается наибольший порядок), например, . Порядок сложности суммы функций определяется как порядок доминанты первого и второго слагаемых (выбирается наибольший порядок), например, 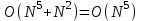 , где k – константа, f и g – функции. , где k – константа, f и g – функции.3.3 Виды функции сложности алгоритмов Время выполнения алгоритма T зависит от объема входных данных N (рисунок 2)  , ,где  – время выполнения алгоритма, мс; – время выполнения алгоритма, мс;N – объем входных данных. Для оценивания трудоемкости алгоритмов введена специальная система обозначений – О-нотация. 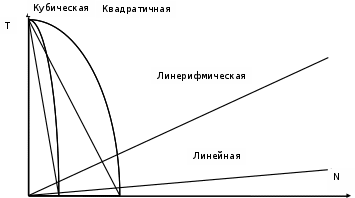 Рисунок 2 – Графики функций сложности алгоритмов Рисунок 2 – Графики функций сложности алгоритмовО-нотация позволяет учитывать в функции f (n) значимые элементы, отбрасывая второстепенные: 1) кубическая функция – функция f(n), старший член которой содержит 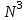 . О-нотация имеет вид . О-нотация имеет вид 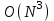 ; ;2) квадратическая функция – функция f(n), старший член которой содержит 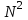 . О-нотация имеет вид . О-нотация имеет вид 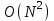 ; ;3) линейная функция – функция f(n), старший член которой содержит 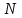 . О-нотация имеет вид . О-нотация имеет вид 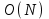 ; ;4) функция линерифмическая – функция, старший член которой равен 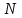 логарифмов логарифмов 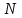 . О-нотация имеет вид . О-нотация имеет вид 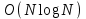 . .Например, в функции 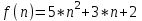 при больших при больших 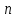 компонента компонента 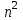 превосходит остальные слагаемые. Поведение функции определяется компонентой превосходит остальные слагаемые. Поведение функции определяется компонентой 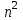 . Остальные компоненты отбрасываются. Функция . Остальные компоненты отбрасываются. Функция 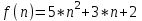 имеет оценку поведения (скорость роста значений) имеет оценку поведения (скорость роста значений) 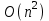 . .О-оценивание позволяет описывать характер поведения функции f(n) с ростом n: насколько быстро или медленно растет эта функция. О-оценка разбивает функции сложности на группы в зависимости от скорости роста: 1) постоянные функции 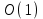 , которые с ростом n не растут; , которые с ростом n не растут;2) функции с логарифмической скоростью роста 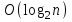 ; ;3) функции с линейной скоростью роста 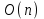 ; ;4) функции с линейно-логарифмической скоростью роста 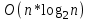 ; ;5) функции с квадратичной скоростью роста 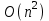 ; ;6) функции со степенной скоростью роста 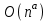 при а>2; при а>2;7) функции с показательной или экспоненциальной скоростью роста 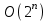 8) функции с факториальной степенью роста  /9/. /9/.Описание О-нотаций приведено в таблице 1. Таблица 1 – Описание О-нотации.
3.4 Сравнение асимптотического поведения функций Математические обозначения для сравнения асимптотического поведения функций имеют вид: 1) определение О большое. Функция 2) определение Омега большое. Функция 3) определение Тета большое. Функция 4) определение о малое. Функция Определение О большое устанавливает, что имеется такая точка Определение Омега большое утверждает, что скорость роста функции Определение Тета большое утверждает, что скорость роста функции Определение о малое утверждает, что скорость роста функции Сравнение асимптотического поведения функций приведено в таблице 2.
Таблица 2 – Относительная скорость роста 1 2 |
