Контрольная работа Алгоритмы и вычислительные методы. Отчет. Курсовая работа по дисциплине Алгоритмы и вычислительные методы оптимизации Выполнил Цема В. И. Группа пб90
 Скачать 385.72 Kb. Скачать 385.72 Kb.
|
|
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации Сибирский государственный университет телекоммуникаций и информатики Межрегиональный учебный центр переподготовки специалистов Курсовая работа по дисциплине: Алгоритмы и вычислительные методы оптимизации Выполнил: Цема В.И. Группа: ПБ-90 Вариант: 0 Проверил: Новосибирск 2022 СодержаниеВведение 2 Задания к курсовой работе 4 Выполнение курсовой работы. 6 1. Переход к канонической форме 6 2. Результаты работы программы 8 3. Листинг программы 10 3. Графический способ 15 4.Составление двойственной задачи к исходной и поиск ее решения на основании теоремы равновесия 17 5. Ответы на вопросы для защиты курсовой работы 20 Вывод 21 Список использованной литературы 22 ВведениеВ настоящее время значительное количество управленческих и прикладных задач, решаются с помощью методов математического программирования. Математическое программирование занимается изучением проблем принятия решений, которые могут быть математически сформулированы как задачи нахождения максимума (минимума) некоторой, вообще говоря, нелинейной функции (целевой функции) многих переменных, при заданной системе ограничений на основные переменные задачи. Задачи программирования связаны с вопросами эффективного использования или распределения ограниченных ресурсов для достижения желаемых целей. Характерной чертой таких задач является большое число решений, удовлетворяющих их основным условиям. Поэтому необходимо уметь находить наилучшее из возможных решений. Выбор наилучшего решения (плана) – называется программированием, а само наилучшее решение называется оптимальным планом. Термин «программирование» в данном случае ничего общего с термином «программирование (т.е. составление программ) для ЭВМ» не имеет, так как дисциплина «линейное программирование» возникла еще до того времени, когда ЭВМ стали широко применяться при решении математических, инженерных, экономических и других задач. Термин «линейное программирование» возник в результате неточного перевода английского «linear programming». Одно из значений слова «programming» - составление планов, планирование. Следовательно, правильным переводом «linear programming» было бы не «линейное программирование», а «линейное планирование», что более точно отражает содержание дисциплины. Однако, термин линейное программирование, нелинейное программирование и т.д. в нашей литературе стали общепринятыми. Наиболее развитыми в области решения оптимизационных задач являются методы линейного программирования. Если ограничения (система уравнений и неравенств) и целевая функция представлены переменными (Х1, Х2,…Хn) в первой степени, т.е. линейны, возникает задача линейного программирования. Если имеет место хотя бы одно нелинейное выражение, то задача относится к нелинейному программированию. Во многих случаях математическое моделирование систем приводит к задачам линейного программирования (ЛП). Задачи линейного программирования в канонической форме широко распространены в инженерной практике, и для их решения разработана большая группа методов, основным из которых является симплекс-метод. Симплекс метод был предложен американским математиком Р.Данцигом в 1947 году, с тех пор для нужд промышленности этим методом нередко решаются задачи линейного программирования с тысячами переменных и ограничений. В последствии этим методом нередко стали решать задачи линейного программирования с тысячами переменных и ограничений. Симплекс-метод является универсальным методом, которым можно решить любую задачу линейного программирования. Одной из задач, поставленных в данной курсовой работе, будет задача по разработке программы, решающей задачу линейного программирования в канонической форме симплекс-методом. Задания к курсовой работеРешение задачи линейного программирования, теория двойственности Перейти к канонической форме задачи линейного программирования. 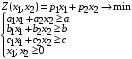 Написать программу, решающую задачу линейного программирования в канонической форме симплекс-методом с выводом всех промежуточных симплексных таблиц. Решить исходную задачу графически и отметить на чертеже точки, соответствующие симплексным таблицам, полученным при выполнении программы из п.1. Составить двойственную задачу к исходной и найти ее решение на основании теоремы равновесия. Ответить на вопросы для защиты курсовой работы. Вариант выбирается по последней цифре пароля.
Выполнение курсовой работы.1. Переход к канонической формеРассмотрим задачу линейного программирования: 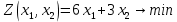 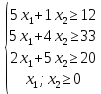 Перейдем к канонической форме записи введя дополнительные переменные с знаком « - » кроме того переходим к целевой функции, подлежащей максимизации. Для этого целевая функция Z умножается на –1.Изменяем знаки коэффициентов целевой функции на противоположные. в неравенства: 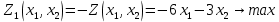 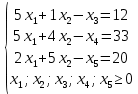 Расширенная матрица системы 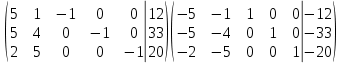 В матрице выделен единичный базис, но базисное решение не является опорным, т.к. в правой части содержатся отрицательные коэффициенты. Поэтому необходимо в каждое уравнение ввести искусственные переменные и решать задачу методом искусственного базиса. В уравнения, не содержащие базисной переменной, добавляем со знаком «+» неотрицательные переменные x6, x7, x8, называемые искусственными. 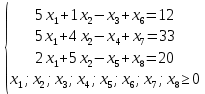 Выразим базисные переменные 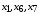 через свободные через свободные 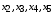 , и приведем их и функцию к специальному виду для составления симплексной таблицы. , и приведем их и функцию к специальному виду для составления симплексной таблицы.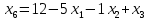 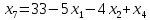 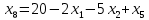 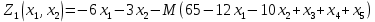 где М – большое положительное число. 2. Результаты работы программы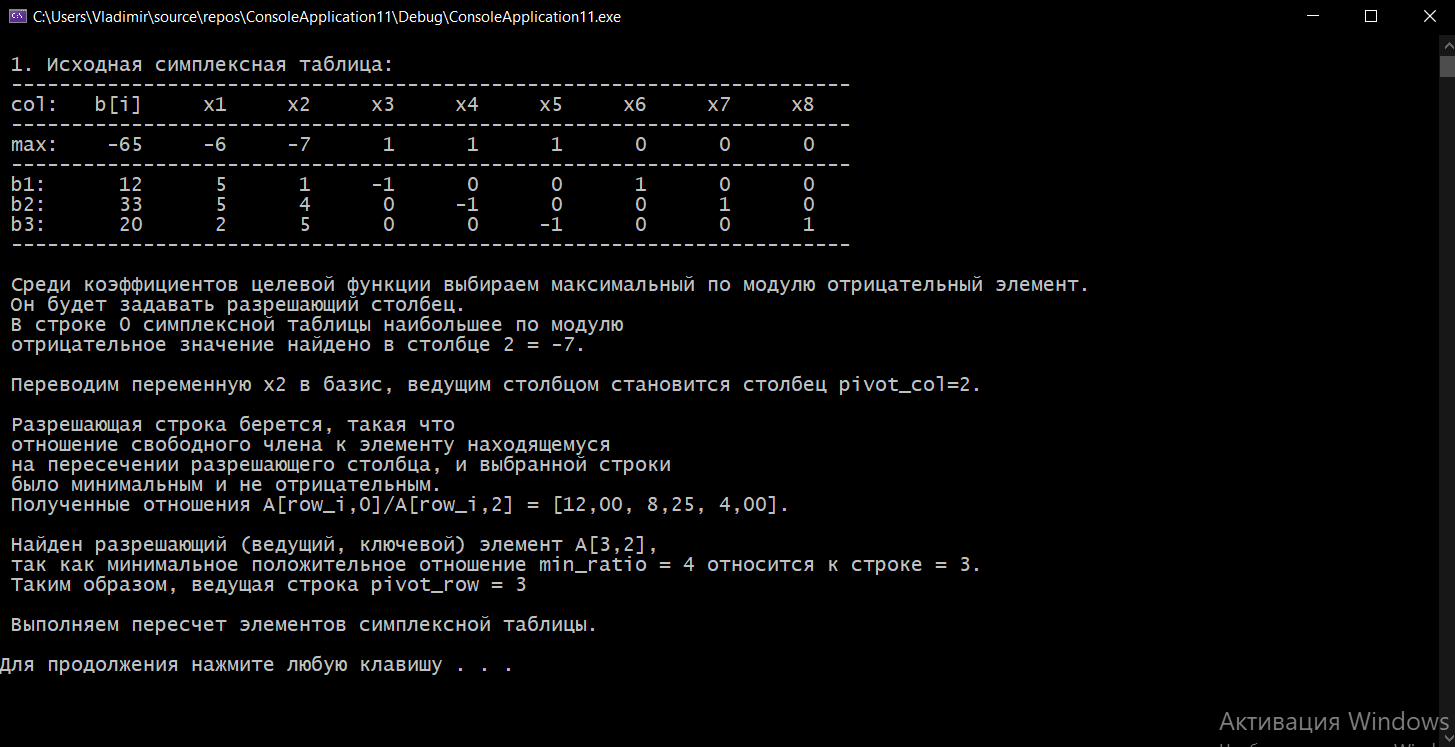 Рисунок 1 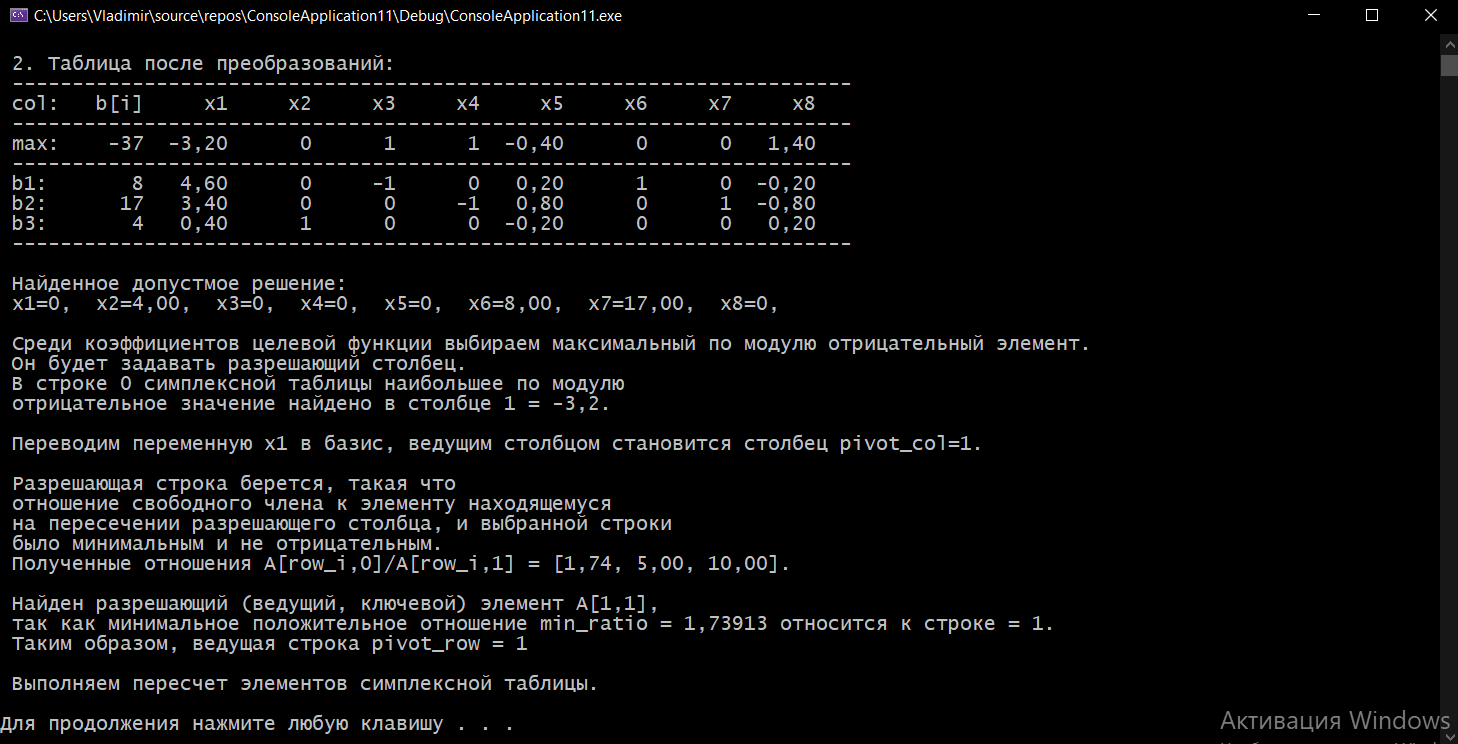 Рисунок 2 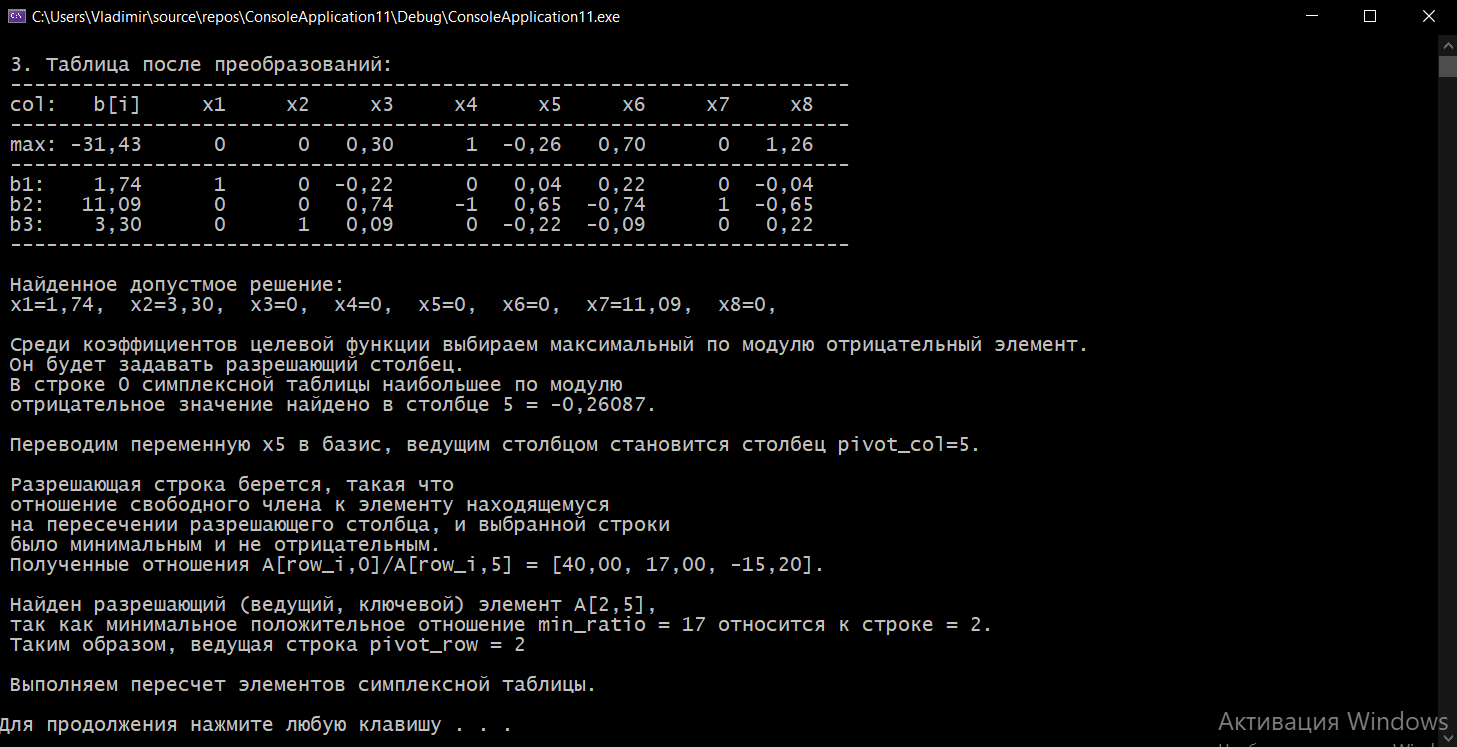 Рисунок 3 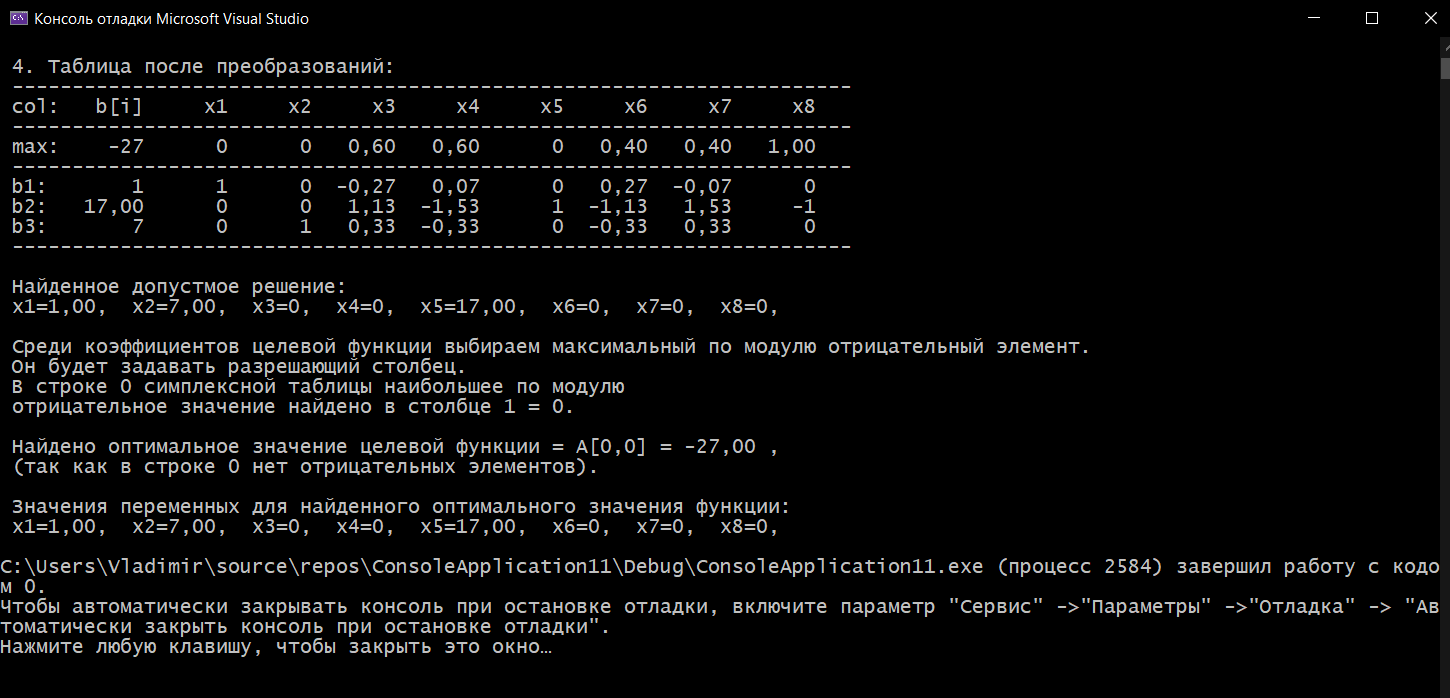 Рисунок 4 Как видно из полученного решения (рис. 4) оптимальное (максимальное) значение целевой функции достигается при следующих значениях переменных: 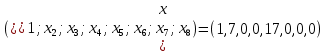 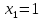 ; ; 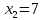 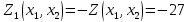 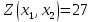 3. Листинг программы#include #include #include #include using namespace std; #define M 100 /* ограничения по количеству строк и столбцов для матрицы с исходными данными */ #define N 100 static const double epsilon = 1.0e-8; int equal(double a, double b) { return fabs(a - b) < epsilon; } typedef struct { int m, n; // m=количество строк в исходных данных, n=количество столбцов, at[m x n] double mat[M][N]; // Двумерный массив для данных } Simplex_table; /* Функция, служащая для печати строки из символов '-' заданной длины */ void print_line(int k) { int j; putchar(' '); for (j = 0; j < k; j++) putchar('-'); putchar('\n'); } /* функция, служащая для вывода на экран симплексной таблицы */ void print_Simplex_table(Simplex_table* tab, const char* mes) { static int counter = 0; int i, j; printf("\n %d. %s:\n", ++counter, mes); print_line(70); printf(" %-6s%5s", "col:", "b[i]"); for (j = 1; j < tab->n; j++) { printf(" x%d", j); } cout << endl; print_line(70); for (i = 0; i < tab->m; i++) { if (i == 0) printf(" max:"); else printf(" b%d: ", i); for (j = 0; j < tab->n; j++) { if (equal((int)tab->mat[i][j], tab->mat[i][j])) printf(" %6d", (int)tab->mat[i][j]); else printf(" %6.2lf", tab->mat[i][j]); } printf("\n"); if (i == 0) print_line(70); } print_line(70); } void pivot_on(Simplex_table* tab, int row, int col) { int i, j; double pivot; /* Обращение к полям производится путем создания составных имён pivot = tab->mat[row][col]; /* Функция assert оценивает выражение, которое передается ей в качестве аргумента, через параметр expression. assert(pivot > 0); for (j = 0; j < tab->n; j++) tab->mat[row][j] /= pivot; assert(equal(tab->mat[row][col], 1.)); for (i = 0; i < tab->m; i++) // Цикл для каждой из оставшихся строк { double multiplier = tab->mat[i][col]; // multiplier - коэффициент if (i == row) continue; for (j = 0; j < tab->n; j++) /* Формула для пересчета элементов таблицы r[i] = r[i] - z * r[row]; */ { tab->mat[i][j] -= multiplier * tab->mat[row][j]; } } } /* Функция для поиска основного (главного) столбца. Критерием выбора служит наибольшее по модулю отрицательное значение столбца в матрице mat[0][1..n] */ int find_pivot_column(Simplex_table* tab) { int j, pivot_col = 1; double lowest = tab->mat[0][pivot_col]; for (j = 1; j < tab->n; j++) { if (tab->mat[0][j] < lowest) { lowest = tab->mat[0][j]; pivot_col = j; } } printf("\n Среди коэффициентов целевой функции выбираем максимальный по модулю отрицательный элемент.\n" " Он будет задавать разрешающий столбец." "\n В строке 0 симплексной таблицы наибольшее по модулю\n" " отрицательное значение найдено в столбце %d = %g.\n\n", pivot_col, lowest); if (lowest >= 0) { return -1; /* Если в строке [0] все столбцы положительные, то базисный план является оптимальным. */ } return pivot_col; } /* Функция для поиска разрешающей строки В качестве разрешающей строки выбирается строка с наименьшим отношением ratio = col[0] / col[pivot] */ int find_pivot_row(Simplex_table* tab, int pivot_col) { int i, pivot_row = 0; double min_ratio = -1; printf("\n Разрешающая строка берется, такая что\n" " отношение свободного члена к элементу находящемуся\n" " на пересечении разрешающего столбца, и выбранной строки\n" " было минимальным и не отрицательным.\n" " Полученные отношения A[row_i,0]/A[row_i,%d] = [", pivot_col); for (i = 1; i < tab->m; i++) { double ratio = tab->mat[i][0] / tab->mat[i][pivot_col]; if (i == (tab->m - 1)) { printf("%3.2lf", ratio); } else { printf("%3.2lf, ", ratio); } if ((ratio > 0 && ratio < min_ratio) || min_ratio < 0) { min_ratio = ratio; pivot_row = i; } } printf("].\n"); if (min_ratio == -1) return -1; printf("\n Найден разрешающий (ведущий, ключевой) элемент A[%d,%d],\n" " так как минимальное положительное отношение min_ratio = %g относится к строке = %d.\n", pivot_row, pivot_col, min_ratio, pivot_row); return pivot_row; } void check_b_positive(Simplex_table* tab) { int i; for (i = 1; i < tab->m; i++) assert(tab->mat[i][0] >= 0); } /* Эта Функция по заданному столбцу единичной матрицы находит строку, содержащую 1. Функция возвращает -1, если столбец не из единичной матрицы. Ищем базисную переменную */ int find_basis_variable(Simplex_table* tab, int col) { int i, xi = -1; for (i = 1; i < tab->m; i++) { if (equal(tab->mat[i][col], 1)) { if (xi == -1) xi = i; // Находим первую '1'. Сохраняем номер содержащей её строки else return -1; // В случае если найдена вторая '1', то матрица не единичная. } else if (!equal(tab->mat[i][col], 0)) { return -1; /* При нахождении элемента отличного от 0 и не равного '1', данный столбец не является столбцом единичной матрицы */ } } return xi; } /* Функция, служащая для выводна на экран оптимального плана */ void print_optimal_vector(Simplex_table* tab, const char* message) { int j, xi; printf(" %s", message); for (j = 1; j < tab->n; j++) // Цикл по каждому столбцу { xi = find_basis_variable(tab, j); if (xi != -1) printf(" x%d=%3.2lf, ", j, tab->mat[xi][0]); else printf(" x%d=0, ", j); } printf("\n"); } void Pauza(); void simplex(Simplex_table* tab) { int loop = 0; check_b_positive(tab); while (++loop) { int pivot_col, pivot_row; pivot_col = find_pivot_column(tab); if (pivot_col < 0) { printf(" Найдено оптимальное значение целевой функции = A[0,0] = %3.2lf ,\n" " (так как в строке 0 нет отрицательных элементов).\n\n", tab->mat[0][0]); print_optimal_vector(tab, "Значения переменных для найденного оптимального значения функции:\n"); break; } printf(" Переводим переменную x%d в базис, ведущим столбцом становится столбец pivot_col=%d.\n", pivot_col, pivot_col); pivot_row = find_pivot_row(tab, pivot_col); if (pivot_row < 0) { printf(" Нет ведущей строки.\n"); break; } printf(" Таким образом, ведущая строка pivot_row = %d\n", pivot_row); printf("\n Выполняем пересчет элементов симплексной таблицы.\n\n", pivot_row); Pauza(); pivot_on(tab, pivot_row, pivot_col); print_Simplex_table(tab, "Таблица после преобразований"); print_optimal_vector(tab, "\n Найденное допустмое решение:\n"); if (loop > 50) { printf("Превышено допустимое число итераций > %d.\n", loop); break; } } } void Pauza() { //printf("\n"); system("pause"); system("CLS"); //Очищаем экран } /* До начала работы программы здесь необходимо ввести все данные для симплексной таблицы */ Simplex_table tab = { 4, 9, { // Размер симплексной таблицы [4 строки x 9 столбцов ] {-65.0, -6.0, -7.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0,}, // Max: z = 9*x1 + 8*x2 - x3 - x4 - x5 - 38 {12.0, 5.0, 1.0, -1.0, 0.0, 0.0, 1.0, 0.0, 0.0,}, // 4*x1 + 1*x2 - x3 + x6 = 9 .. b1 {33.0, 5.0, 4.0, 0.0, -1.0, 0.0, 0.0, 1.0, 0.0,}, // 3*x1 + 2*x2 - x4 + x7 = 13 .. b2 {20.0, 2.0, 5.0, 0.0, 0.0, -1.0, 0.0, 0.0, 1.0,}, // 2*x1 + 5*x2 - x5 + x8 = 16 .. b3 } }; /// /////////////////////////////////////////////////////////// int main() { setlocale(LC_ALL, "rus"); //отображение кириллицы в консоле SetConsoleCP(1251); SetConsoleOutputCP(1251); print_Simplex_table(&tab, "Исходная симплексная таблица"); simplex(&tab); /* здесь знак & обозначает операцию получения адреса объекта, а не его значения */ /* Оператор getch(); заставит программу ждать нажатия любой клавиши */ //_getch(); return 0; } 3. Графический способРешим исходную задачу графически. Каждое неравенство исходной системы ограничений определяет полуплоскость. Запишем уравнения граничный прямых для этих полуплоскостей.
Построим прямые по двум точкам. 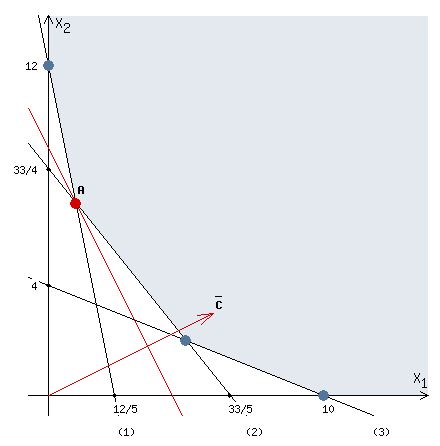 Каждая прямая разбивает плоскость на две полуплоскости. Для выбора полуплоскостей, определяемых каждым неравенством, подставим координаты «пробной» точки (0;0) в каждое неравенство. Получаем: 50 + 10 12 не верно. Следовательно, отмечаем полуплоскость, не содержащую «пробную» точку (0;0). 50 + 40 33 не верно. Следовательно, отмечаем полуплоскость, не содержащую «пробную» точку (0;0). 20 + 50 20 не верно. Следовательно, отмечаем полуплоскость, не содержащую «пробную» точку (0;0). Найдем пересечение отмеченных полуплоскостей с учетом условия: х1, х2 0. Выделим серым цветом получившийся неограниченный четырёхугольник- область допустимых решений системы ограничений. Построим линию уровня Z = 0: 6х1 + 3х2 = 0
Вектор grad Z = (6;3) определяет направление наибольшего возрастания функции Z. Построим из начала координат вектор 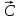 =grad Z = (6;3). Этот вектор также показывает направление наибольшего возрастания функции. =grad Z = (6;3). Этот вектор также показывает направление наибольшего возрастания функции.Перемещая линию уровня параллельным переносом в направлении вектора 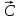 , находим первую точку пересечения линии уровня и заштрихованного четырехугольника – точку A. Эта точка является точкой минимума функции. Точка A получается в результате пересечения прямых (1) и (2). Для нахождения ее координат решим уравнения: , находим первую точку пересечения линии уровня и заштрихованного четырехугольника – точку A. Эта точка является точкой минимума функции. Точка A получается в результате пересечения прямых (1) и (2). Для нахождения ее координат решим уравнения: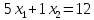 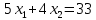 Находим решение системы: 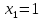 , , 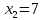 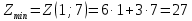 4.Составление двойственной задачи к исходной и поиск ее решения на основании теоремы равновесияПравила построения двойственной задачи по имеемой прямой задаче: 1) Если прямая задача решается на максимум, то двойственная задача решается на минимум; если прямая задача решается на минимум то двойственная на максимум; 2) В задаче на максимум ограничения неравенства имеют вид ≤, а в задаче на минимум 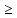 ; ;3) Количество переменных двойственной задачи соответствует количеству ограничений исходной задачи; 4) Коэффициенты при неизвестных в целевой функции исходной задачи являются правыми частями в ограничениях двойственной задачи и, наоборот, правые части ограничений исходной задачи являются коэффициентами при неизвестных в целевой функции двойственной задачи; 5) Матрица коэффициентов при неизвестных в системе ограничений двойственной задачи является транспонированной матрицей коэффициентов при неизвестных в системе ограничений исходной задачи; 6) Условия неотрицательности в обоих задачах сохраняются. Составим двойственную задачу для исходной. 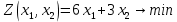 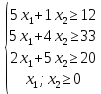 Матрица коэффициентов системы ограничений имеет вид: 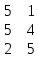 Транспонируем эту матрицу. Чтобы найти транспонированную матрицу поменяем ряды и столбцы исходной матрицы местами. Получаем: 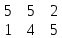 Двойственная задача имеет вид: 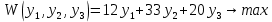 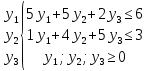 Прямая и обратная задачи линейного программирования связаны между собой теоремами двойственности. Первая теорема двойственности. Если одна задача из пары двойственных обладает оптимальным решением, то и другая имеет оптимальное решение, причем экстремальные значения соответствующих целевых функций равны. 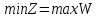 Если же хотя бы одна из задач не имеет допустимого решения, то ни одна из них не имеет оптимального решения. 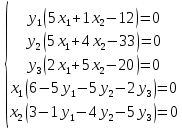 Подставим в составленную систему оптимальное решение исходной задачи: x1 = 1, x2 = 7. 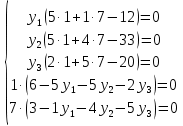 Произведение равно нулю, если один из множителей равен 0. Получаем 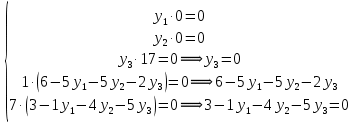 Тогда, 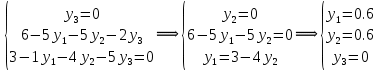 Оптимальное решение двойственной задачи Wmax = W(0.6; 0.6; 0). По теореме о минимаксе Zmin = Wmax = 27. Окончательно, Wmax = W(0.6; 0.6; 0) = 27. 5. Ответы на вопросы для защиты курсовой работы 1. В какой форме приведена исходная задача линейного программирования? В стандартной (или симметричной) форме. 9. Какая переменная называется искусственной, когда она вводится и какой коэффициент соответствует ей в функции? Искусственные переменные вводятся после приведения исходной задачи к канонической форме, а в функцию добавляется достаточно большой коэффициент M, который имеет смысл штрафа за введение искусственных переменных. 11. Как определяется разрешающий элемент при использовании искусственного базиса? Как в обычном симплекс методе используя: 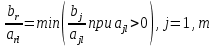 15. Как определить количество переменных при составлении двойственной задачи? Если в прямой задаче система ограничений содержит m строк, то в двойственной задаче будет m переменных. ВыводПри выполнении данной курсовой работы был изучен симплекс-метод решения задач линейного программирования, который является универсальным методом, позволяющим решить любую задачу линейного программирования. Для применения симплекс метода исходная задача была предварительно приведена к задаче линейного программирования в канонической форме. Далее на языке программирования C была разработана программа, решающая задачу линейного программирования в канонической форме симплекс-методом. Исходная задача первоначально решалась с помощью введения искусственного базиса и двухэтапного симплекс-метода. В дальнейшем эта же задача была решена при помощи графического метода. В ходе выполнении курсовой работы изучена технология составления двойственной задачи и найдено ее решение на основании теоремы равновесия. При этом получены равные экстремальные значения целевых функций прямой и двойственной задач. В результате выполнения заключительного этапа работы найдены ответы на поставленные вопросы. Файл с исходным текстом программы «simplex.c» и исполняемый файл «simplex.exe» прилагаются к отчету. Список использованной литературыМ.Ю. Галкина Лекции по курсу «Алгоритмы и вычислительные методы оптимизации». М.Ю. Галкина Методические указания к курсовой работе «Решение задачи линейного программирования, теория двойственности». Гераськин М.И. Линейное программирование: учеб. пособие / М.И. Гераськин, Л.С. Клентак; под общ. ред. Л.С. Клентак. – Самара: Изд-во СГАУ, 2014. – 104 с. Методы решения задач линейного программирования. Методические указания к лабораторным работам по курсу «Модели и методы в экономике» / Казань: КГАСУ. Сост.: Ф. Г. Ахмадиев, Д. К. Галиуллин, Р. М. Гильфанов Казань, 2008. – 45 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
