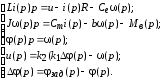Моделирование импульсной САУ. Курсач. Курсовая работа по дисциплине Цифровые системы управления Тема Анализ и синтез импульсной системы управления Вариант 2 магистрант гр. 14081115 Ануфриев Д. А
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
|
Министерство образования и науки РФ Федеральное государственное образовательное учреждение высшего образования «Тульский государственный университет» Институт высокоточных систем им. В.П. Грязева Кафедра «Приборы управления» Курсовая работа по дисциплине «Цифровые системы управления» Тема: «Анализ и синтез импульсной системы управления» Вариант № 2 Выполнил: магистрант гр.140811/15 Ануфриев Д.А. Проверил: к.т.н. кафедры ПУ Телухин С.В. Тула 2022 г. ЗАДАНИЕ«Система автоматического управления» 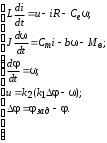
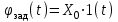 ; ; 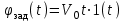 . .1 АНАЛИЗ ИМПУЛЬСНОЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯМатематическая модель системы автоматического управления имеет вид:
Операторная форма уравнений имеет вид:
Проведем преобразование первого уравнения системы 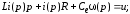 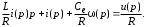 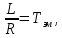 где 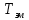 – электромагнитная постоянная времени. – электромагнитная постоянная времени.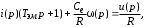 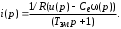 Для второго уравнения системы 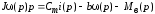 при 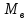 = 0 имеем = 0 имеем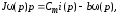 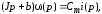 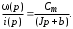 Исходя из проведенных проеобразований, структурная схема системы автоматического управления имеет вид, приведенный на рисунке 1 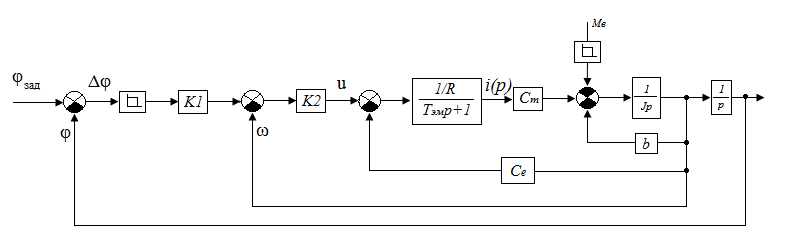 Рисунок 1 – Структурная схема системы автоматического управления Получим передаточную функцию двигателя при 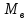 = 0 и выполним следующие преобразования = 0 и выполним следующие преобразованияТогда передаточная функция двигателя имеет вид: Wдв(p) записать Получим передаточную функцию замкнутого контура Wк(p) Далее получим непрерывную передаточную функцию прямой цепи, связывающую φ(p) и 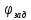 (p) (p) Wнепрерывн(p) Разложим разомкнутую передаточную функцию на множители 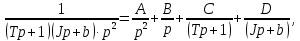 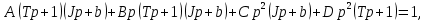 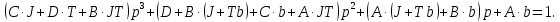 Система уравнений для нахождения A, B, C, D имеет вид: 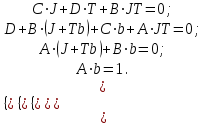 (3) (3)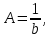 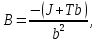 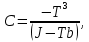 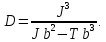 Импульсная передаточная функция разомкнутой системы имеет вид: 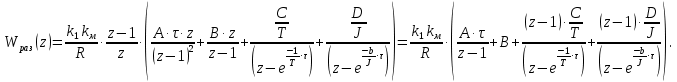 Подставляем A, B, C, D 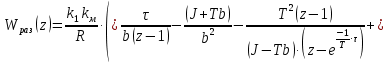 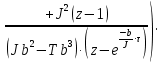 Подставляем значения 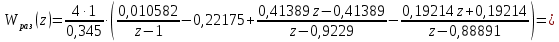 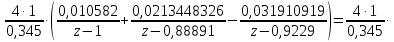 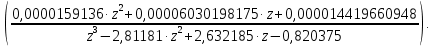 Импульсная передаточная функция замкнутой системы имеет вид: 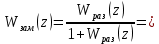 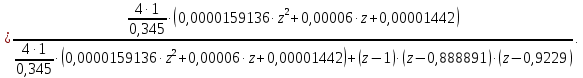 Импульсная передаточная функция ошибки системы имеет вид: 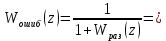 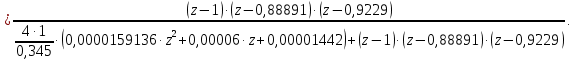 Структурная схема импульсной системы с экстраполятором нулевого порядка приведена на рисунке 2. 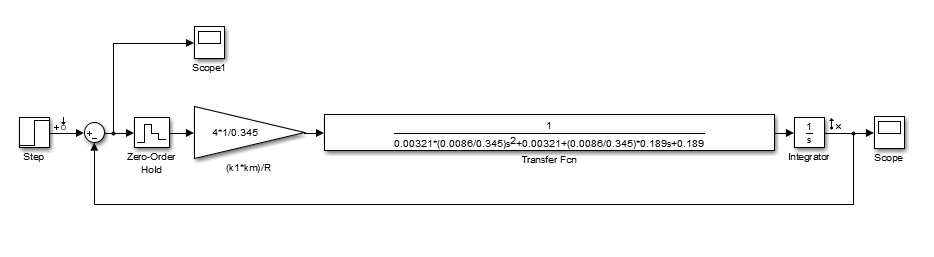 Рисунок 2 – Структурная схема импульсной системы Имитационная модель импульсной системы приведена на рисунке 3. 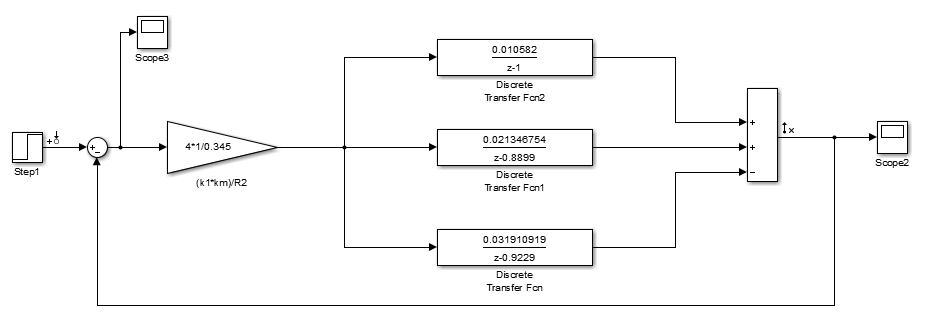 Рисунок 3 - Имитационная модель импульсной системы Годограф Найквиста приведен на рисунке 4 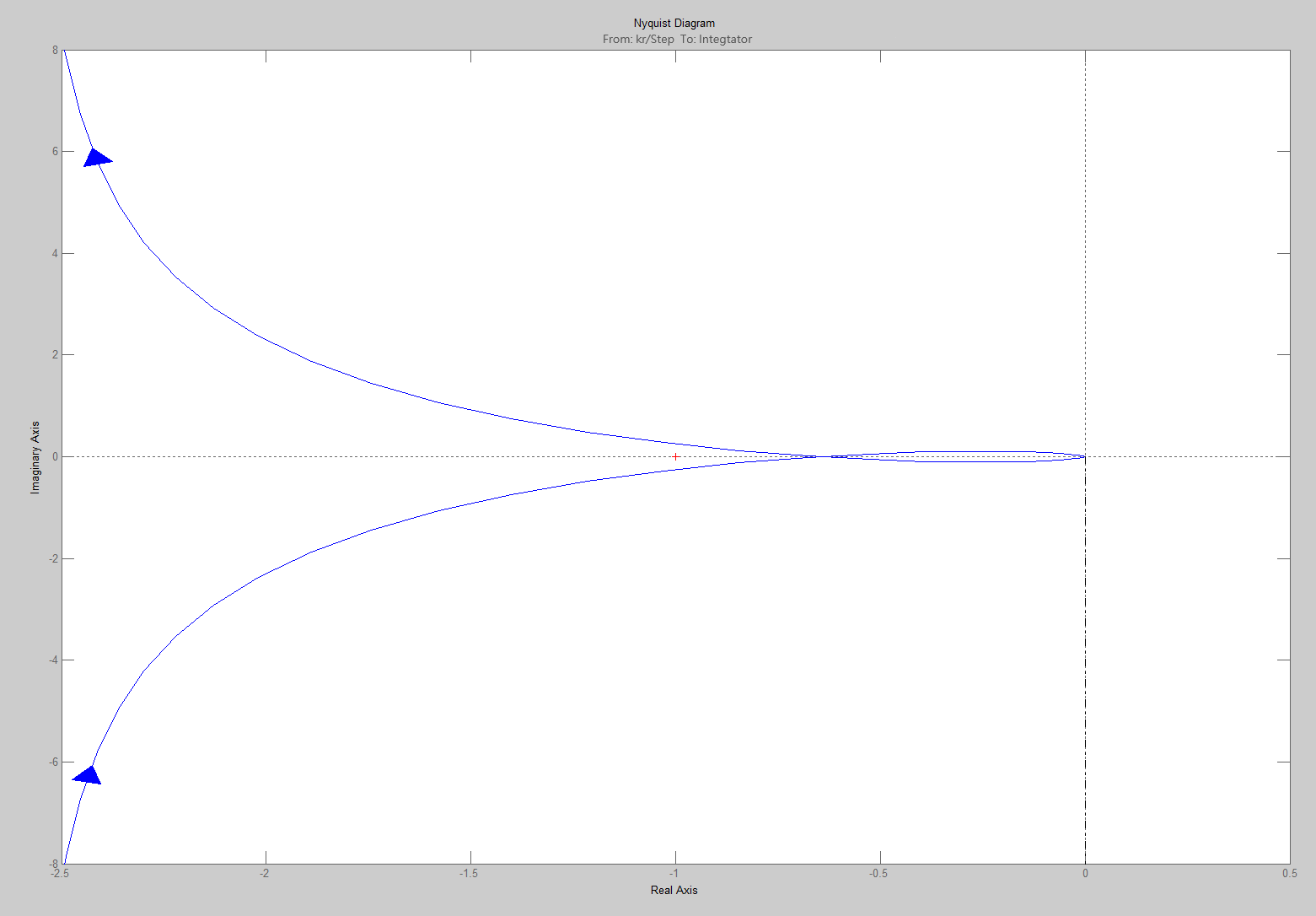 Рисунок 4 – Годограф Найквиста На годографе видно, что точка (-1;0) не охватывается, следовательно по критерию Найквиста система устойчива. ЛАФЧХ разомкнутой импульсной системы приведена на рисунке 5. 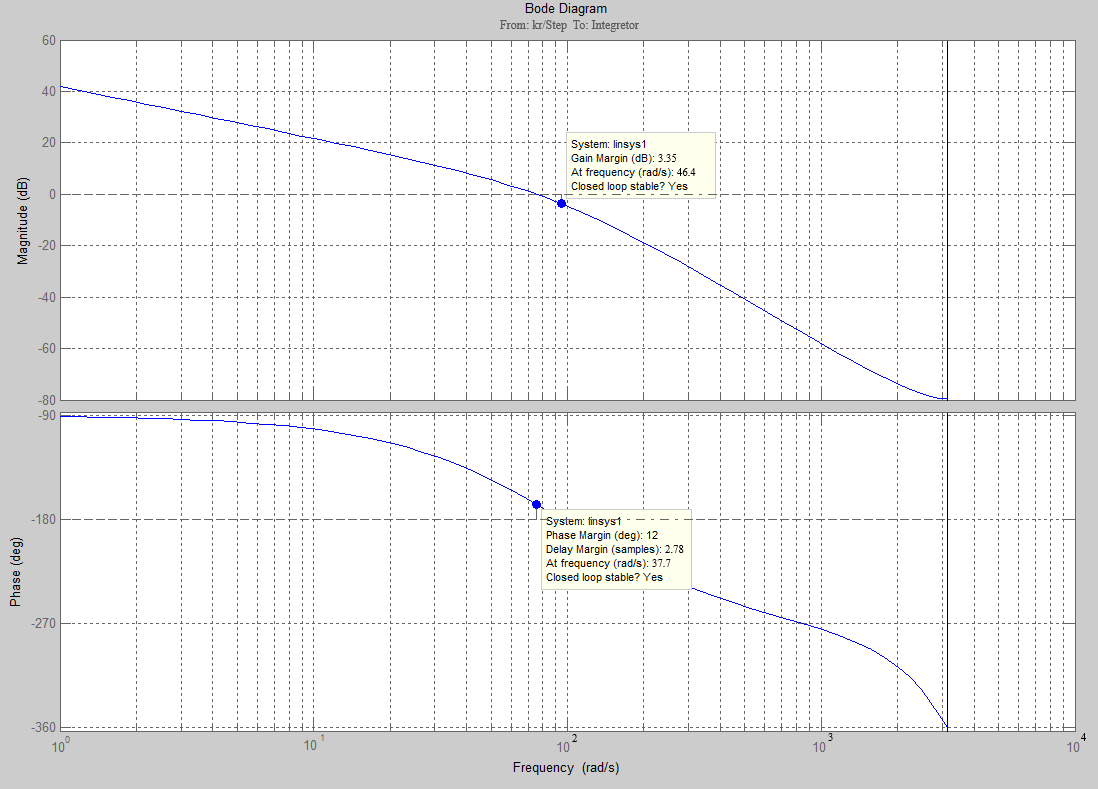 Рисунок 5 – ЛАФЧХ разомкнутой импульсной системы Система имеет запас устойчивости по фазе 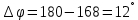 и запас по амплитуде и запас по амплитуде 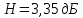 . .ЛАФЧХ замкнутой импульсной системы приведена на рисунке 6. 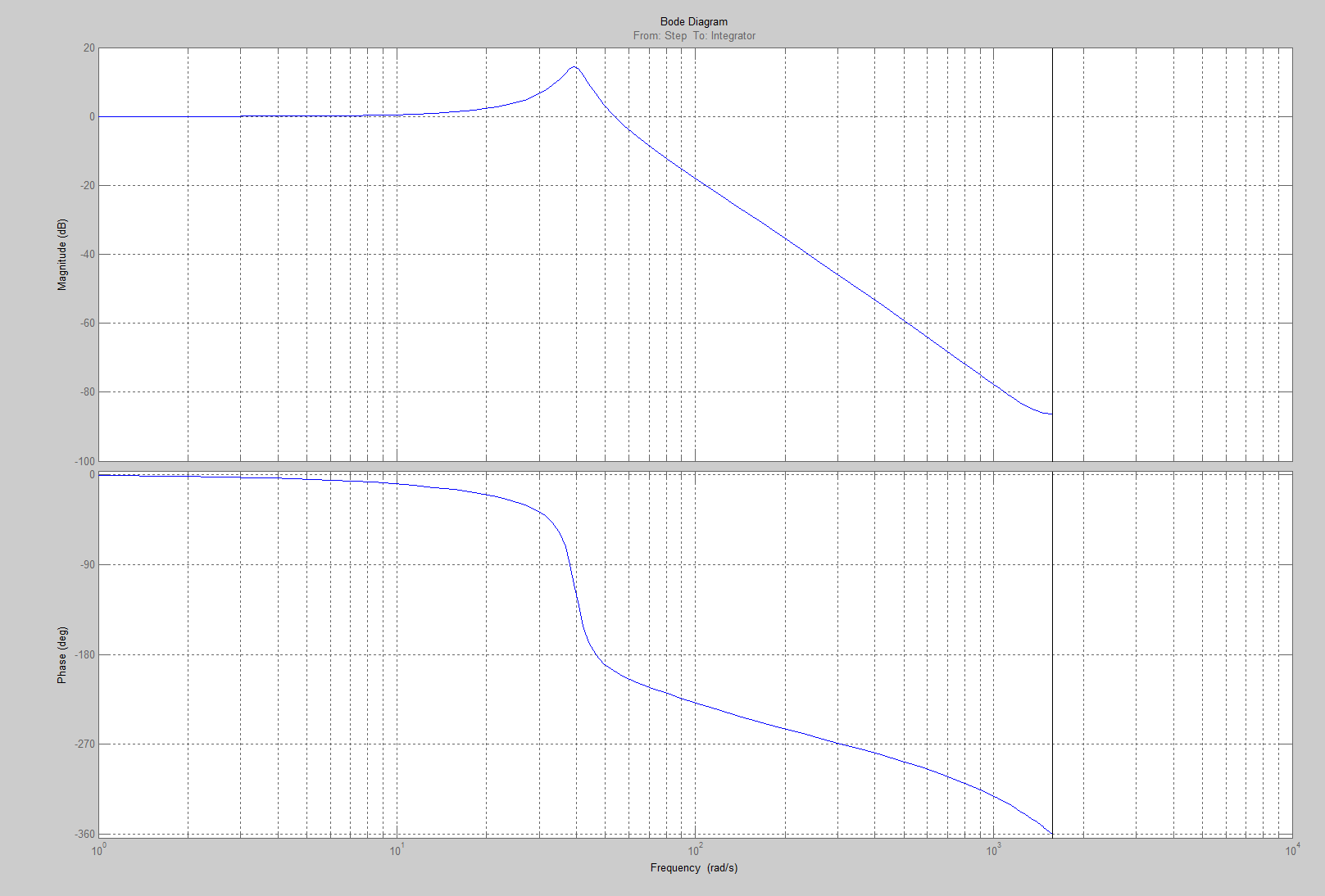 Рисунок 6 – ЛАФЧХ замкнутой импульсной системы Для построения псевдочастотных характеристик разомкнутой и замкнутой системы необходимо произвести замену: 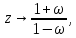 вместо 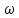 подставляем подставляем 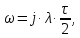 где 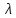 – псевдочастота. – псевдочастота.Графики псевдочастотных характеристик разомкнутой системы приведены на рисунках 7,8. 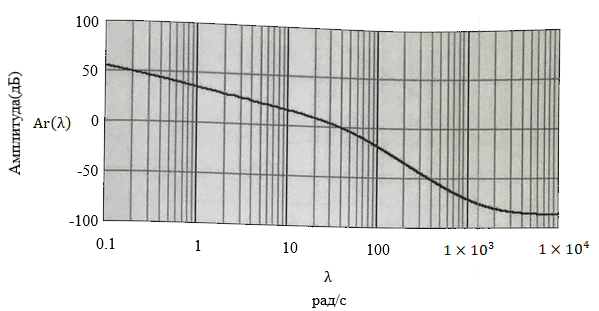 Рисунок 7 – Амплитудная псевдочастотная характеристика разомкнутой системы 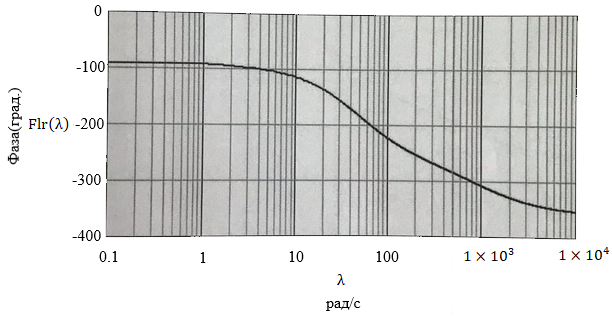 Рисунок 8 – Фазовая псевдочастотная характеристика разомкнутой системы Графики псевдочастотных характеристик замкнутой системы приведены на рисунках 9,10. 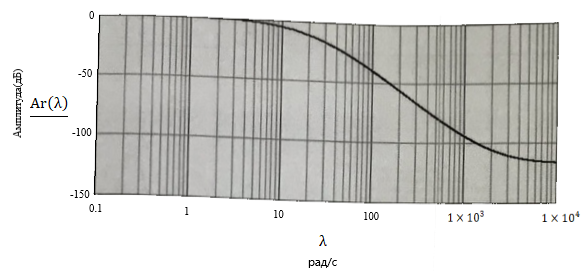 Рисунок 9 – Амплитудная псевдочастотная характеристика замкнутой системы 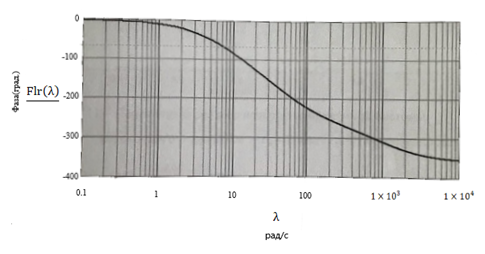 Рисунок 10 – Фазовая псевдочастотная характеристика замкнутой системы График переходного процесса нескорректированной системы приведен на рисунке 11. 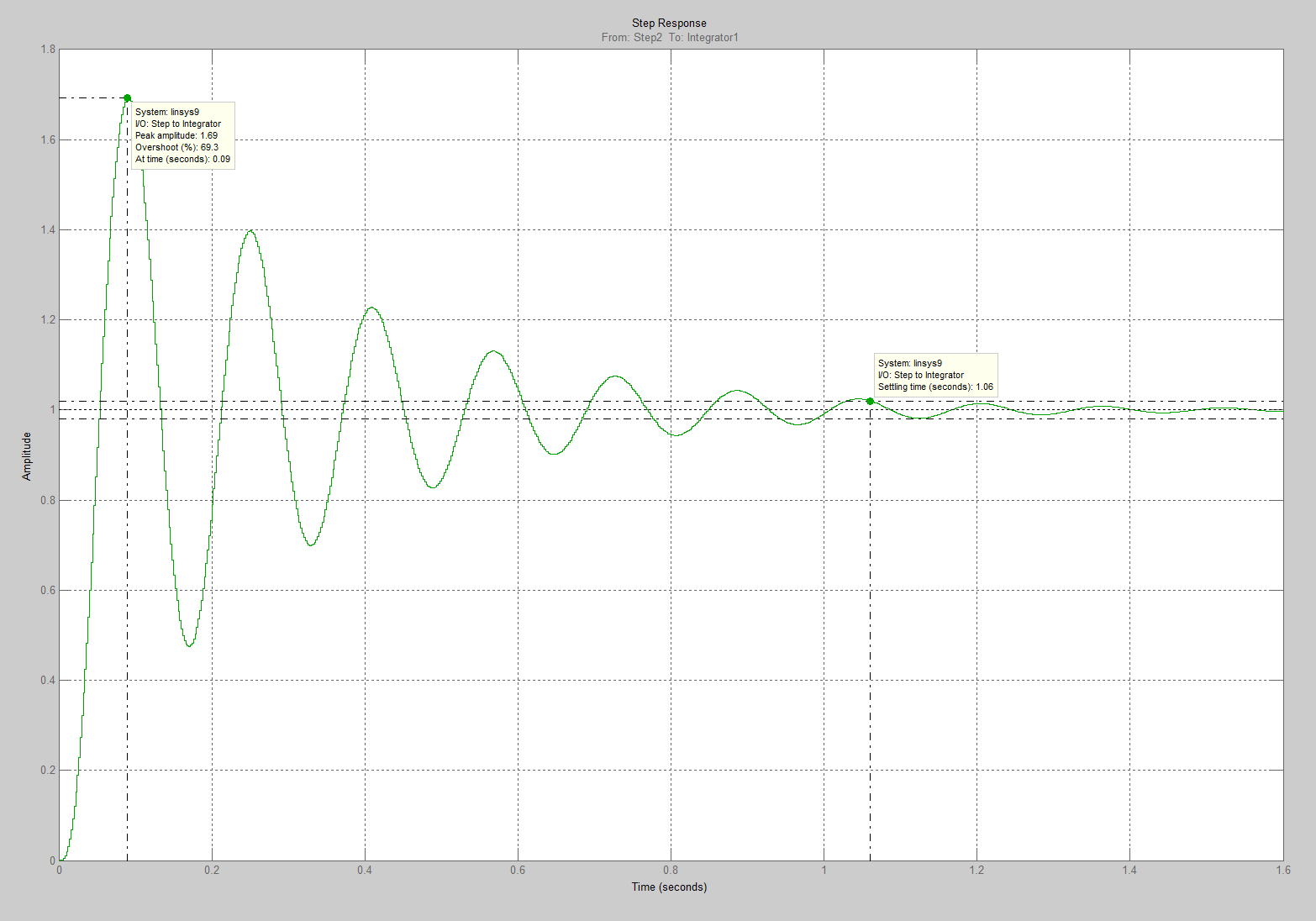 Рисунок 11 – Переходный процесс нескорректированной системы Время переходного процесса 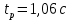 , а перерегулирование , а перерегулирование 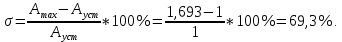 Теорема о конечном значении оригинала имеет вид: 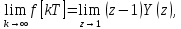 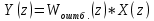 , ,где 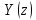 – выходной сигнал, – выходной сигнал, 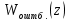 – передаточная функция ошибки, – передаточная функция ошибки, 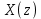 – входной сигнал. – входной сигнал.По заданию входной нарастающий сигнал записывается как 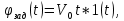 где 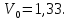 Входной сигнал имеет вид: 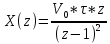 , ,Выходной сигнал имеет вид: 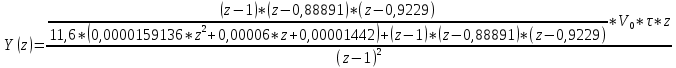 , ,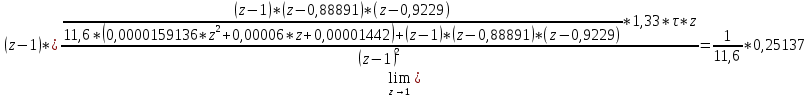 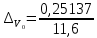 , ,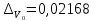 . .График ошибки нескорректированной системы приведён на рисунке 12 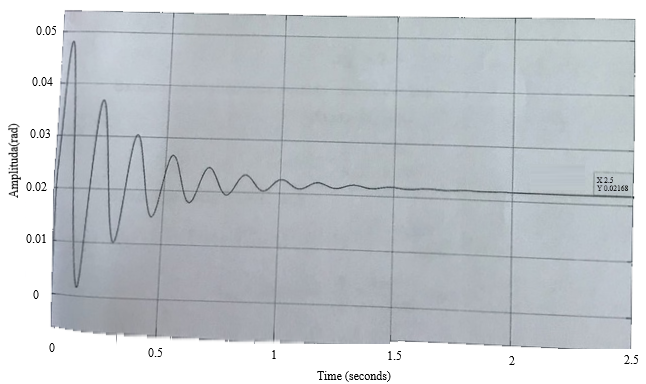 Рисунок 12 – График ошибки нескорректированной системы Установившиеся значение ошибки составляет 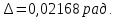 Входное ступенчатое воздействие записывается как 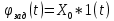 , ,где 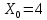 Входной сигнал имеет вид: 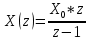 , ,Входной сигнал имеет вид: 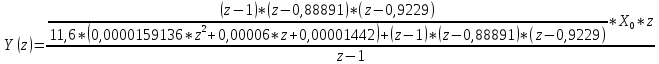 , ,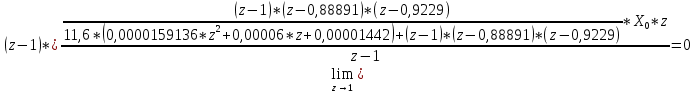 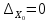 . .Входное возмущающее воздействие имеет вид: 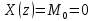 , ,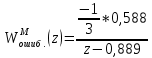 , ,Выходной сигнал имеет вид: 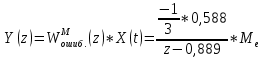 , ,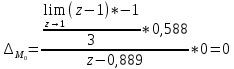  2 Синтез системы автоматического управленияК системе автоматического управления по заданию предъявляются следующие требования: 1)Время переходного процесса 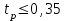 c c2)Перерегулирование 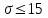 % %3)Ошибка 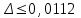 рад радИсходная система не удовлетворяет данным требованиям, поэтому она нуждается в коррекции. Коэффициент передачи системы автоматического управления имеет вид 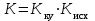 , ,где 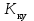 – коэффициент корректирующего устройства, – коэффициент корректирующего устройства, 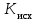 – коэффициент исходной системы. – коэффициент исходной системы.Коэффициент корректирующего устройства должен удовлетворять условию 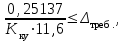 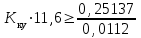 , ,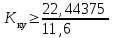 , ,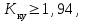 Выбираем 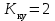 . .Структурная схема непрерывной системы с экстраполятором нулевого порядка и коэффициентом корректирующего устройства приведена на рисунке 13.  Рисунок 13 – Структурная схема непрерывной системы с экстраполятором нулевого порядка и коэффициентом корректирующего устройства Имитационную модель импульсной системы с коэффициентом корректирующего устройства приведена на рисунке 14. 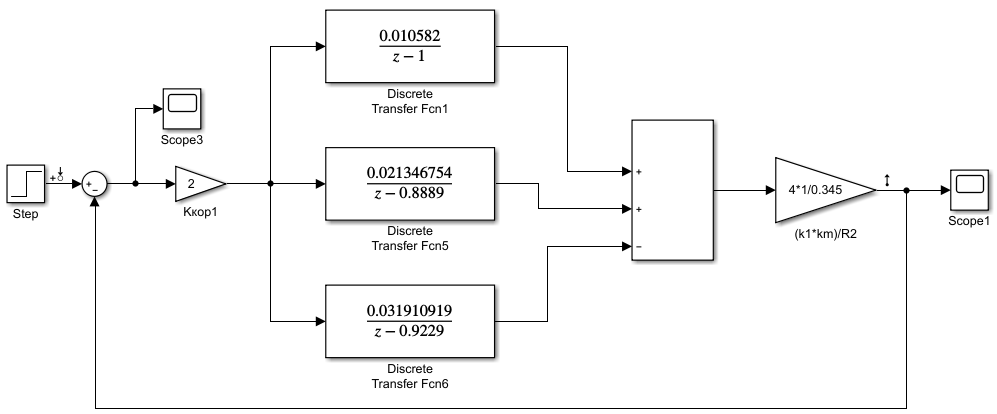 Рисунок 14 – Имитационную модель импульсной системы с коэффициентом корректирующего устройства Г 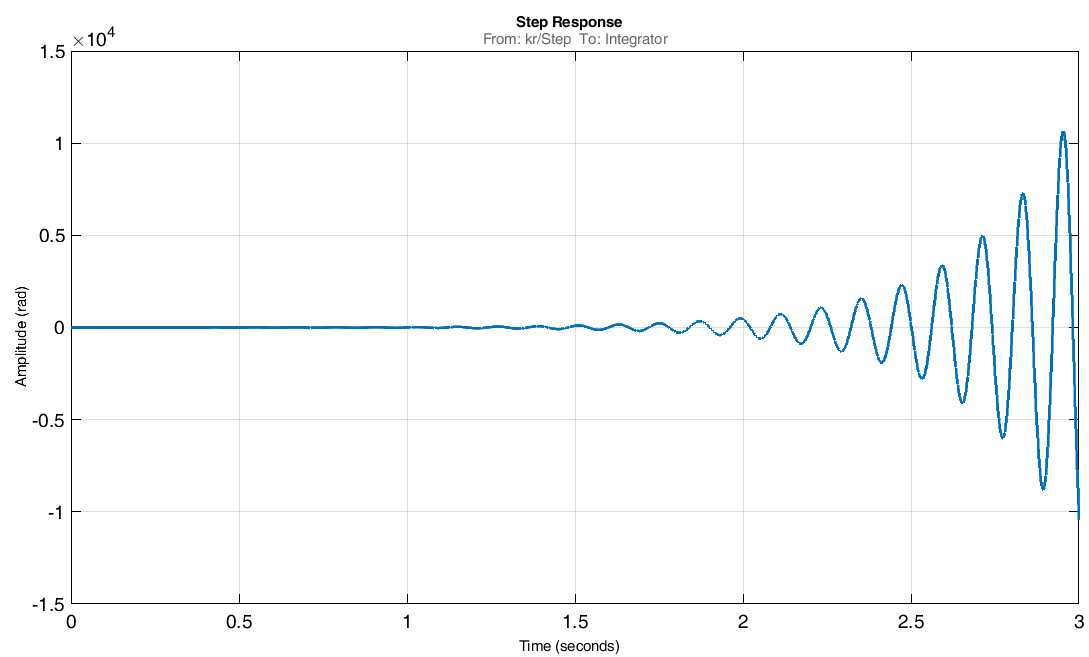 рафик переходного процесса приведён на рисунке 15. рафик переходного процесса приведён на рисунке 15.Рисунок 15 – График переходного процесса с коэффициентом коррекции Из графика видно, что система неустойчива. Следовательно, требуется ввести дополнительно передаточную функцию корректирующего устройства. Для того чтобы найти передаточную функцию корректирующего устройства необходимо построить желаемую ЛАФЧХ и вычесть из неё реальную ЛАФЧХ. В результате получится ЛАФЧХ корректирующего устройства по которой можно определить передаточную функцию. Желаемый коэффициент передачи разомкнутой должен быть больше 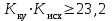 . .Частота среза разомкнутой системы должна быть не менее 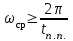 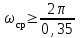 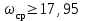 рад/с рад/сЖ 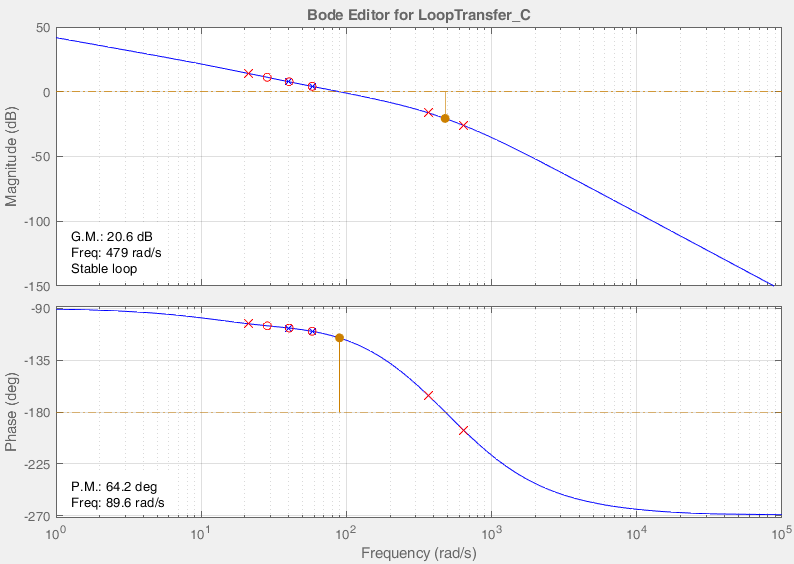 елаемая ЛАФЧХ разомкнутой системы приведена на рисунке 16 елаемая ЛАФЧХ разомкнутой системы приведена на рисунке 16Рисунок 16 – График желаемой ЛАФЧХ разомкнутой системы Передаточная функцию корректирующего устройства приведена на рисунке 17.  Рисунок 17 – Передаточная функцию корректирующего устройства Имитационная модель импульсной системы с корректирующим устройством приведена на рисунке 18. Р  исунок 18 – Имитационная модель импульсной системы с корректирующим устройством исунок 18 – Имитационная модель импульсной системы с корректирующим устройствомГ 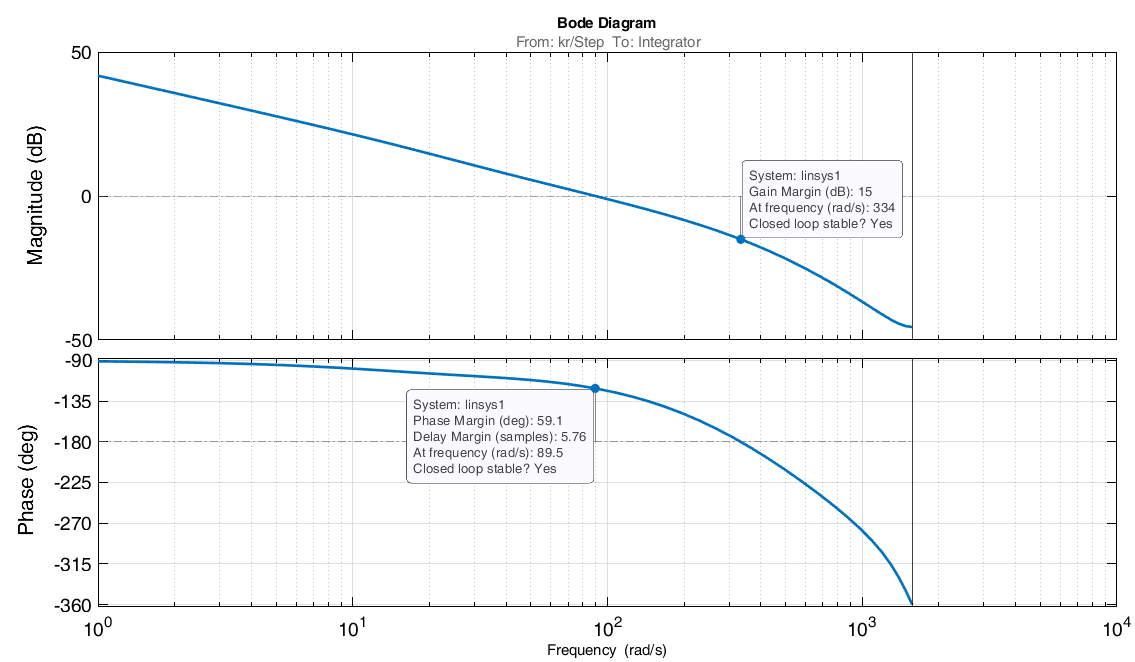 рафик ЛАФЧХ разомкнутой импульсной системы с корректирующим устройством приведён на рисунке 19. рафик ЛАФЧХ разомкнутой импульсной системы с корректирующим устройством приведён на рисунке 19.Рисунок 19 – ЛАФЧХ разомкнутой импульсной системы с корректирующим устройством Запас устойчивости по фазе равен 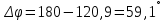 , запас по амплитуде , запас по амплитуде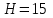 дБ. дБ.График ЛАФЧХ замкнутой импульсной системы с корректирующим устройством приведён на рисунке 20. Р 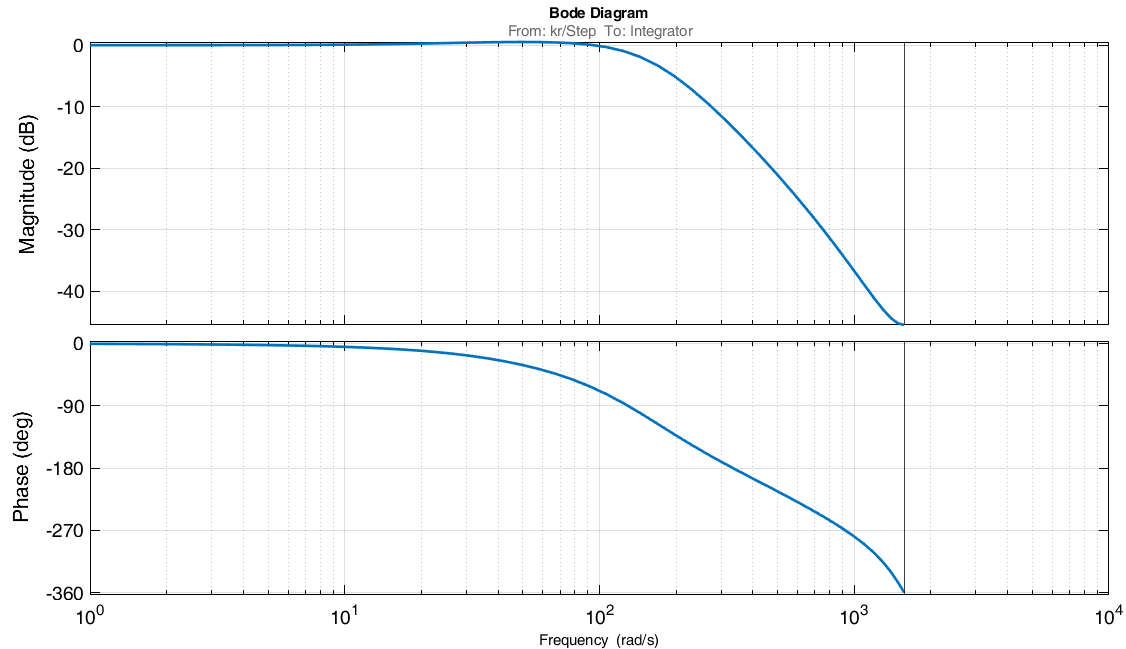 исунок 20 – ЛАФЧХ замкнутой импульсной системы с корректирующим устройством исунок 20 – ЛАФЧХ замкнутой импульсной системы с корректирующим устройствомГрафик переходного процесса импульсной системы с корректирующим устройством приведён на рисунке 21. 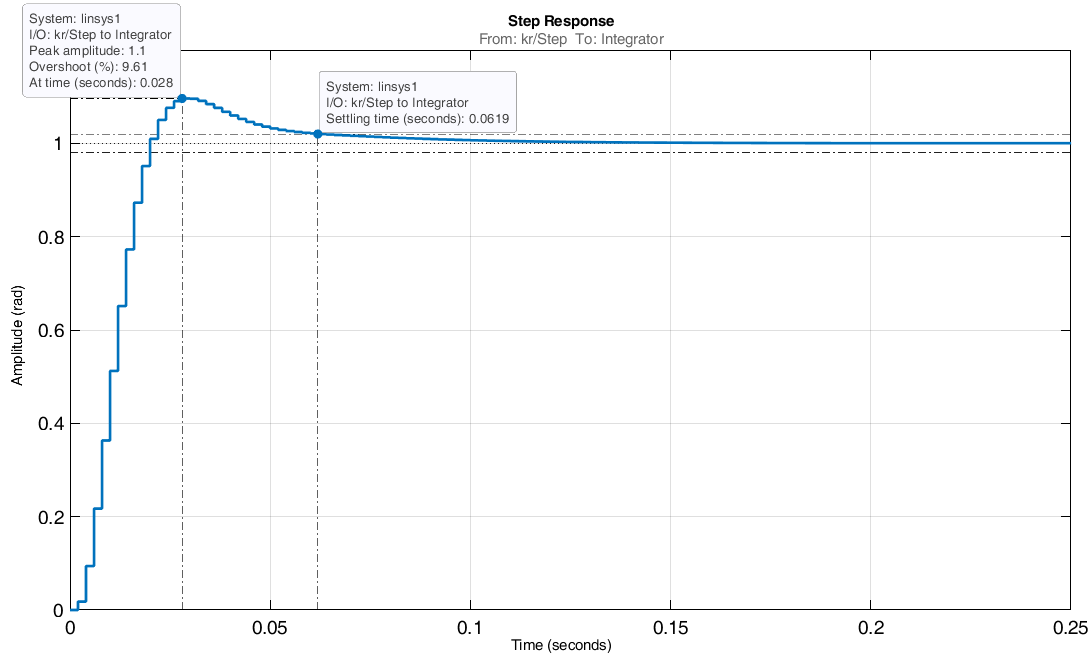 Рисунок 21 – График переходного процесса импульсной системы с корректирующим устройством Рисунок 21 – График переходного процесса импульсной системы с корректирующим устройствомИз графика видно что время переходного процесса 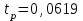 c, а перерегулирование c, а перерегулирование 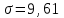 %. %.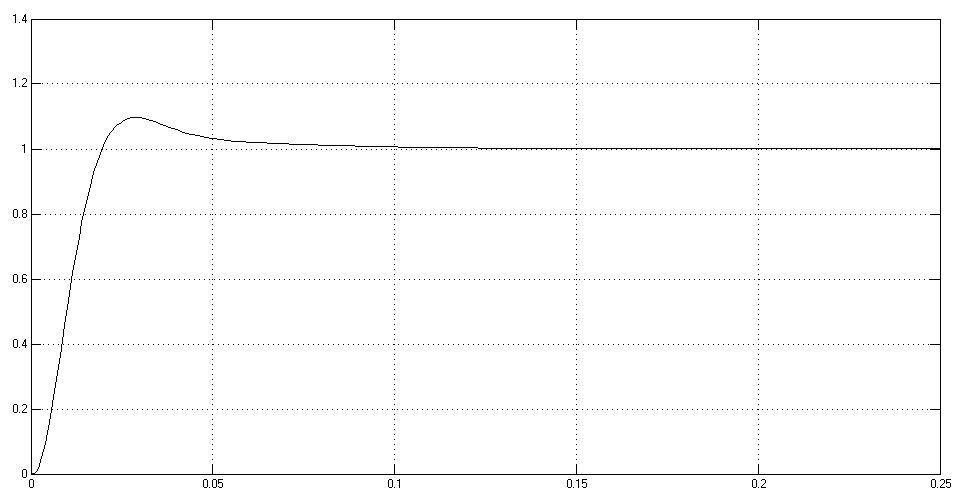 Рисунок 22 – График непрерывной импульсной системы с корректирующим устройством График ошибки импульсной системы с корректирующим устройством приведён на рисунке 23. 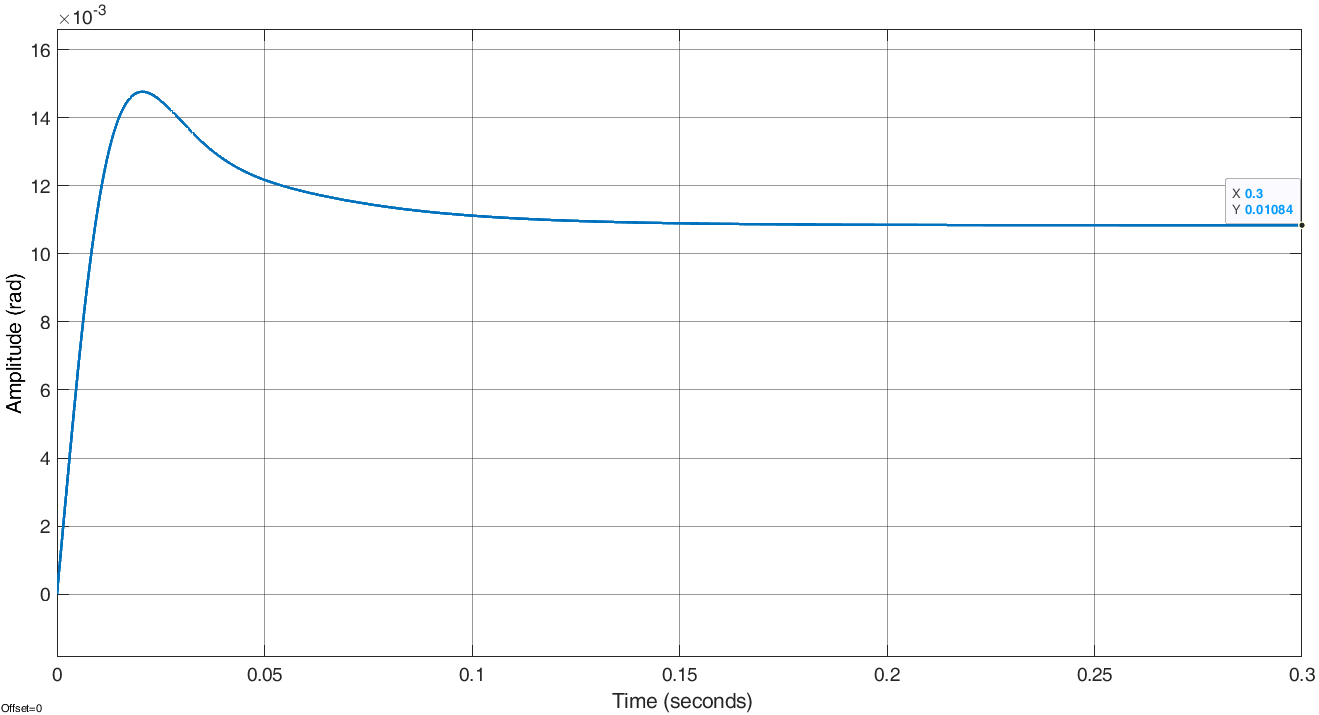 Рисунок 23 – График ошибки импульсной системы с корректирующим устройством Рисунок 23 – График ошибки импульсной системы с корректирующим устройствомУстановившееся значение ошибки составляет 0,01084 рад и удовлетворяет требованиям задания. ЗаключениеПроведен анализ и синтез импульсной системы автоматического управления. Получены передаточные функции, логарифмические амплитудно-фазовые частоты и псевдочастотные характеристики. Построены графики передаточных процессов и ошибок импульсной системы автоматического управления. В результате синтеза в скорректированной системе запас устойчивости по фазе равен 59,1̊ , запас устойчивости по амплитуде равен 15 дБ. Время переходного процесса равно 0,0619 секунд, а перерегулирование 9,61%. Установившееся значение ошибки равно 0,01084 рад. Системы удовлетворяет заданию. Список литературы1. Бесекерский В.А. Теория систем автоматического управления: [Учебное издание] / В.А. Бесекерский, Е.П. Попов. – 4-е изд., перераб. и доп. – СПб.: Профессия, 2004. – 752 с. 2. Пупков К.А. Методы классической и современной теории автоматического управления: учебник для вузов: в 5 т. Т.1. Математические модели, динамические характеристики и анализ систем автоматического управления / К.А. Пупков [и др.]; под ред. К.А. Пупкова, Н.Д. Егупова. – 2-е изд., перераб. и доп. – М.: МГТУ им. Баумана, 2004. – 656 с. 3. Пупков К.А. Методы классической и современной теории автоматического управления: учебник для вузов: в 5 т. Т.2. Статистическая динамика и идентификация систем автоматического управления / К.А. Пупков [и др.]; под ред. К.А. Пупкова, Н.Д. Егупова. – 2-е изд., перераб. и доп. – М.: МГТУ им. Баумана, 2004. – 640 с. 4. Пупков К.А. Методы классической и современной теории автоматического управления: учебник для вузов: в 5 т. Т.5. Методы современной теории автоматического управления / К.А. Пупков [и др.]; под ред. К.А. Пупкова, Н.Д. Егупова. – 2-е изд., перераб. и доп. – М.: МГТУ им. Баумана, 2004. – 784 с. 5. Ким Д.П. Сборник задач по теории автоматического управления. Линейные системы: учеб. пособие для вузов / Д.П. Ким, Н.Д. Дмитриева. – М.: ФИЗМАТЛИТ, 2007. – 168 с. 6. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – М.: Наука, 1975. – 768 с. 7. Сборник задач по теории автоматического регулирования и управления / Под ред. В.А. Бесекерского. – М.: Наука, 1978. – 512 с. 8. Иващенко Н.Н. Автоматическое регулирование. – М.: Машиностроение, 1978. – 736 с. 9. Васильев Д.В., Чуич В.Г. Системы автоматического управления (примеры расчета). – М.: Высш. школа, 1967. – 418 с. 10. Руководство по проектированию систем автоматического управления / Под ред. В.А. Бесекерского. – М.: Высшая школа, 1983. – 269 с. 11. Задачник по теории автоматического управления / Под ред. А.С. Шаталова. – М.: Энергия, 1979. – 490 с. 12. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал), 2-е изд. – М.: Машиностроение, 1982. – 504 с. |

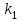 [В/рад]
[В/рад]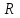 [Ом]
[Ом]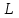 [Гн]
[Гн]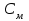 [Нм/А]
[Нм/А]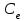 [Вс/рад]
[Вс/рад]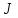 [Ом]
[Ом]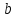 [Нм∙с/рад]
[Нм∙с/рад]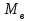 [Нм]
[Нм]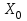
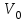
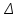
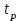 [с]
[с]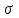 [%]
[%]