КР Физика НГ пласта. Курсовая работа По дисциплине Физика нефтяного и газового пласта
 Скачать 459.4 Kb. Скачать 459.4 Kb.
|
|
Коэффициент разгазирования – количество газа, выделившегося из единицы объёма нефти при снижении давления на единицу. При движении газа по пласту наблюдается т.н. дроссельный эффект – уменьшение давления газового потока при его движении через сужения в каналах. При этом наблюдается изменение температуры. Интенсивность изменения температуры при изменении давления характеризуется коэффициентом Джоуля-Томсона: Т=·Р, (40) где Т – изменение температуры: – коэффициент Джоуля-Томсона (зависит от природы газа, давления, температуры); Р – изменение давления. Плотность пластовой нефти зависит от состава нефти, давления, температуры, количества растворённого газа (рис. 6.). Чем меньше плотность нефти, тем выше выход светлых фракций. Не все газы, растворяясь в нефти, одинаково влияют на её плотность. С повышением давления плотность нефти значительно уменьшается при насыщении её углеводородными газами. Плотность нефтей при насыщении азотом или углекислым газом несколько возрастает с увеличением давления. Обычно плотность нефтей колеблется в пределах 820-950 кг/м3. 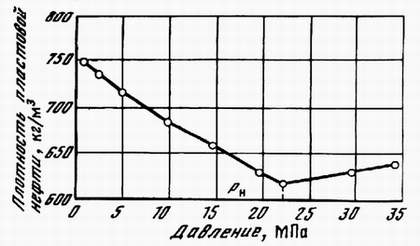 Рис. 6. Изменение плотности пластовой нефти в зависимости от давления Вязкость – сила трения (внутреннего сопротивления), возникающая между двумя смежными слоями внутри жидкости или газа на единицу поверхности при их взаимном перемещении (рис. 7). Динамическая вязкость определяется через закон Ньютона: 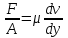 , (41) , (41)где А – площадь перемещающихся слоёв жидкости (газа) – см. рис. 3.2; F – сила, требующаяся для поддержания разницы скоростей движения между слоями на величину dv; dy – расстояние между движущимися слоями жидкости (газа); dv – разность скоростей движущихся слоёв жидкости (газа). 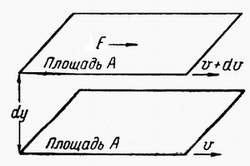 Рис. 7. Движение двух слоёв жидкости относительно друг друга. 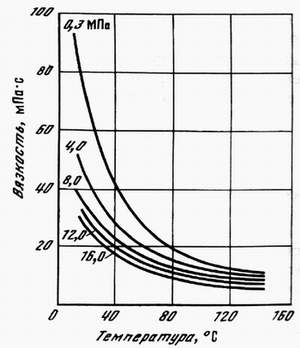 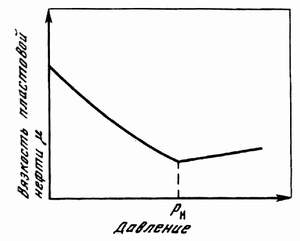 Рис. 8. Изменение вязкости пластовой нефти в зависимости от давления и температуры Вязкость пластовой нефти всегда значительно отличается от вязкости сепарированной вследствие большого количества растворённого газа, повышенного давления и температуры (рис. 8). При этом вязкость уменьшается с повышением количества газа в нефти и с увеличением температуры; повышение давления вызывает увеличение вязкости. Вязкость нефти в пластовых условиях различных месторождений изменяется от сотен мПас до десятых долей мПас. В пластовых условиях вязкость нефти может быть в десятки раз меньше вязкости сепарированной нефти. С вязкостью связан ещё один параметр – текучесть – величина обратная вязкости: 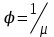 . (42) . (42)Кроме динамической вязкости для расчётов используют также кинематическую вязкость – свойство жидкости оказывать сопротивление перемещению одной части жидкости относительно другой с учётом силы тяжести. 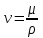 . (43) . (43)Нефть, как и все жидкости, обладает упругостью, т.е. способностью изменять свой объём под действием внешнего давления. Уменьшение объёма характеризуется коэффициентом сжимаемости (или объёмной упругости) : 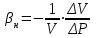 . (44) . (44)Коэффициент сжимаемости зависит от давления, температуры, состава нефти и газового фактора. Нефти, не содержащие растворённого газа, обладают сравнительно низким коэффициентом сжимаемости (0,4-0,7 ГПа-1), а лёгкие нефти со значительным содержанием растворённого газа – повышенным коэффициентом сжимаемости (до 14 ГПа-1). Высокие коэффициенты сжимаемости свойственны нефтям, находящимся в пластовых условиях, близких к критическим. С количеством растворённого газа в нефти также связан объёмный коэффициент b, характеризующий соотношение объёмов нефти в пластовых условиях и после отделения газа на поверхности: 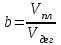 , (45) , (45)где Vпл – объём нефти в пластовых условиях; Vдег – объём нефти при атмосферном давлении и температуре 20С после дегазации. Используя объёмный коэффициент, можно определить усадку нефти (U), т.е. уменьшение объёма пластовой нефти при извлечении её на поверхность (в %): 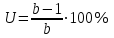 , (46) , (46)Ж) Единицы измерения проницаемости, пористости, вязкости нефти, межфазного натяжения. Единица измерения проницаемости – м2 или мкм2=1 Да. Пористость – безразмерная величина, д.ед или проценты. Размерность динамической вязкости: система СИ – [Пас] система СГС – [Пуаз]=[г/(смс)] Единицы измерения кинематической вязкости: система СИ – [м2/с] система СГС – [Стокс] Межфазное натяжение измеряется в Н/м. РАСЧЕТНАЯ ЧАСТЬ Задание 1. Состав газа и его использование для нахождения физических характеристик Определить степень отклонения природной газоконденсатной смеси от закона идеального газового состояния при следующих исходных данных: Т=310 К, Р=14 МПа, относительная плотность газа ρ=1,12; объем газа, добываемого с 1 м3 нефти при р0=0,1 МПа и Т0=273 К – V0=60 м3/м3. Таблица 4. Состав углеводородной части газа.
Решение. Рпр=14/4,98=2,81 Тпр=310/278,9=1,111 По графикам Брауна-Катца zг=0,64. По уравнению состояния Редлиха-Квонга a2=0,4278∙278,92,5/(4,98∙3102,5)=0,065 b=0,0867∙278,9/(4,98∙310)=0,016 (a2-b2p-b)p=0,656 a2bp2=0,202 z3-z2+0,656z-0,202=0 z=0,6 Средняя молекулярная масса газа M=28,14 кг/кмоль 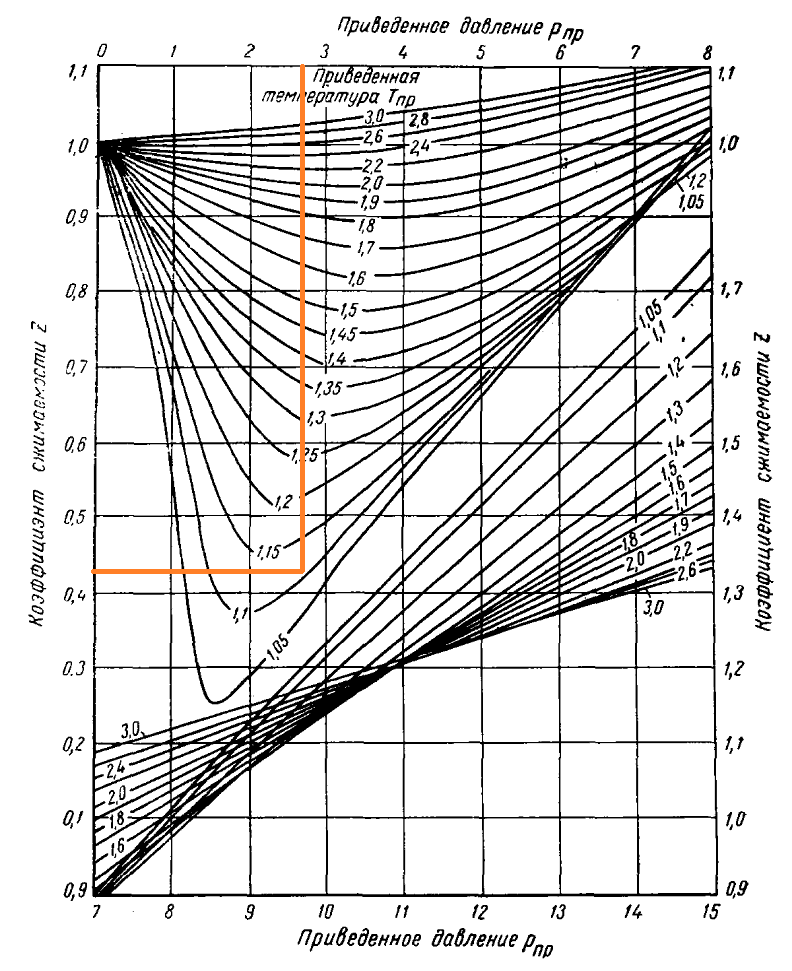 Рис. 9. График Брауна-Катца. Для расчета z методом Гафарова лучше всего подходят условия 0 1,17<Тпр<2,0 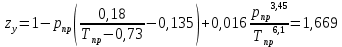 Плотность газа: при нормальных условиях ρг0=Mi/22,414=28,14/22,414=1,255 кг/м3 при стандартных условиях ρгст=Mi/24,05=28,14/24,05=1,170 кг/м3 Относительная плотность газа по воздуху ρ=Mi/29,98=28,14/29,98=0,938 кг/м3 Плотность газа при р=14 МПа и Т=310 К ρг=ρг0РТ0/(zP0T)=1,255∙14∙273/0,6/0,1/310=258 кг/м3. Объем газа, добываемый с 1 м3 нефти V=V0zp0T/(PT0)=60∙0,6∙0,1∙310/14/273=0,292 м3/м3. Задание 2. Основные зависимости расхода жидкости через поры, капилляр, трещину В образце породы размером 10х10х10 см имеется три вида пустот: поры, трещина, капилляр. Известны проницаемость пор матрицы, радиус капилляра, вязкость жидкости, общий расход жидкости через образец, проницаемость породы за счет пор, градиент давления. Найти расход жидкости в образце через поры, капилляр, трещину; раскрытость трещины, трещинную проницаемость. Сравнить расход жидкости через поры, капилляр, трещину. Расчет проводить в системе СИ. Таблица 5. Исходные данные для расчета.
Решение Площадь образца 100 см2=0,01 м2. Расход флюида через поры: Q1=KF/µ∙dp/dx=4∙10-15∙0,01/0,001∙34000=13,6∙10-10 м3/с Расход флюида через капилляр: Q2= 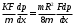 =1∙(0,00002)2/(8∙0,001)∙(3,14∙0,000022/4)∙34000= =1∙(0,00002)2/(8∙0,001)∙(3,14∙0,000022/4)∙34000==2,14∙10-12 м3/с Остаток расхода флюида – это его расход через трещину. Q3=7∙10-6-(13,6∙10-10 +2,14∙10-12 )=7 ∙10-6 м3/с Расход флюида через трещину 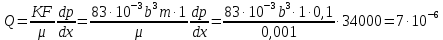 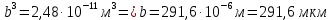 Ктр=83∙10-3∙b2m=83∙10-3∙0,00029162∙1=7,06∙10-9 м2=7058,6 Д. ВЫВОДЫ Приведен литературный обзор по видами пористости и проницаемости пород, зависимости коллекторских свойств от давления; статистические методы отображения неоднородности коллекторских свойств пород. Рассмотрены Методы определения относительных фазовых проницаемостей, коллекторские свойства трещиноватых пород. Приведены данные о составе природных газов и их свойствах, коэффициенте сверхсжимаемости смеси газов и методах его расчета, плотности природного газа, давлении насыщения и растворимости природных газов в нефтях; плотности и вязкости газированных нефтей, объемном коэффициенте, плотности и усадке нефти в пластовых условиях. Приведены единицы измерения проницаемости, пористости, вязкости нефти, межфазного натяжения. Рассчитан коэффициент сверхсжимаемости природного газа 3 способами: по номограммам Брауна-Катца, по уравнению состояния Редлиха-Квонга, по эмпирическим уравнениям Гафарова. Найдена плотность газа при нормальных, стандартных условиях и при действующих давлении и температуре. Определен объем газа, добываемого с 1 м3 нефти. Найдены расход жидкости в образце через поры, капилляр, трещину, раскрытость трещины, трещинная проницаемость. СПИСОК ЛИТЕРАТУРЫ Виноградов В.Г., Дахнов А.В. Практикум по петрофизике. - М, «Недра», 1990. - 287c. Мирзаджанзаде А.Х. Физика нефтяного и газового пласта. – М, «Недра», 1992. - 305c. Гиматудинов Ш.К. Физика нефтяного и газового пласта. – М, «Недра», 1982. - 351c. |
