ППД Практическая работа 1 Ерин ГБ18-03Б. Определение нефтеотдачи в зависимости от упругих свойств жидкости и породы
 Скачать 137.99 Kb. Скачать 137.99 Kb.
|
|
Определение нефтеотдачи в зависимости от упругих свойств жидкости и породы Однородная по проницаемости и толщине пласта нефтяная залежь, ограниченная контуром нефтеносности и площадью F, окружена кольцевой законтурной водонапорной областью с площадью F1. В процессе разработки средневзвешенное давление внутри нефтеносной части залежи изменилось от начального пластового давления до давления насыщения. За тот же промежуток времени средневзвешенное давление в законтурной водонапорной части пласта уменьшилось на величину Δp1. Задание 1: Определить нефтеотдачу, которую можно получить из залежи за счет упругих свойств среды внутри контура нефтеносности и в законтурной части пласта. Исходные данные приведены в табл. 1. Таблица 1 - Таблица исходных данных
РЕШЕНИЕ 1. Коэффициент сжимаемости нефти определяется через начальный объем нефти в залежи Vн0 и объем нефти при давлении насыщения Vн1 (в итоге используем определение объемного коэффициента b): 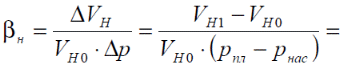 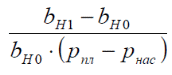 (1.1) (1.1)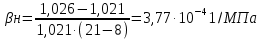 2. Коэффициент упругоемкости пласта (или сжимаемости пористой сжимаемость насыщающих ее жидкостей нефти c насыщенностью (1-S) и воды с насыщенностью S, а также сжимаемость породы: 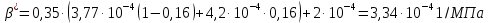 3. Используя коэффициент b* и объем залежи Vзал, вычислим объем нефти, извлекаемый под действием упругих сил внутри контура нефтеносности F: 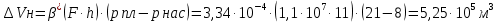 4. Подсчитаем начальные запасы нефти в залежи:  5. Вычислим нефтеотдачу, обусловленную действием только упругих сил внутри контура нефтеносности F: 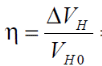 (1.5) (1.5)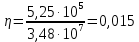 6. Падение давления в пределах контура нефтеносности F нарушит равновесие в пласте, поэтому часть воды под действием упругой энергии законтурной части пласта F1 поступит в нефтеносную область. Коэффициент упругоемкости (сжимаемости) пористой среды в законтурной обводненной части пласта F1 учитывает суммарную сжимаемость породы и насыщающей ее воды: 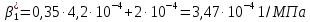 7. Используя коэффициент b*1, найдем количество воды ΔVВ, которое оступит в нефтеносный контур F и вытеснит равную по объему нефть под действием упругих сил при изменении давления Δp1 в законтурной части пласта F1: 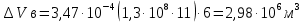 8. Вычисляется нефтеотдача, обусловленная суммарным действием упругих сил: 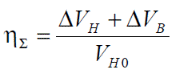 (1.8) (1.8)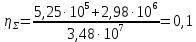 Прогнозирование изменения давления на контуре нефтяного месторождения при упругом режиме в законтурной области пласта При разработке месторождения важно знать изменение давления во времени на условном контуре нефтеносности месторождения pКОН=pКОН(t). Оно позволяет прогнозировать перевод отдельных скважин с фонтанного на механизированные способы эксплуатации, а также определять время, когда пластовое давление снизится до давления насыщения, начнется разгазирование нефти в пласте и возникнет режим растворенного газа, а затем – газонапорный. Таким образом, важно знать, в течение какого периода времени допустимо разрабатывать нефтяное месторождение без воздействия на пласт при упругом режиме, не доводя до возникновения режимов растворенного газа и газонапорного. Глубокозалегающее небольшое по размерам нефтяное месторождение, контур нефтеносности которого имеет форму, близкую к форме круга, окружено обширной водоносной областью, во много раз превосходящей по размеру месторождение. При разработке месторождения нефть будет вытесняться водой, поступающей из законтурной области, где реализуется упругий режим. Считается, что в пределах нефтяной залежи режим жестко водонапорный. Исходные данные приведены в табл.2. Количество воды qЗВ, поступающей из законтурной части месторождения в его нефтенасыщенную часть, определяется по закону, изображенному на (рис. 1.1). 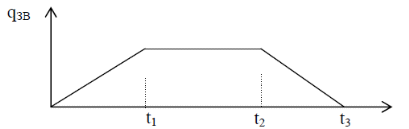 Рис. 1.1. Количество поступившей в залежь законтурной воды 1) В период 0 ≤ t≤ t1 - разбуривания месторождения qЗВ=αt. 2) В период t1 < t≤ t2- стабилизации отбора жидкости qЗВ= q = const . 3) В период t2< t≤ t3 - падения отбора жидкости qЗВ= q- αt. Задание 2: Определить изменение контурного давления при разработке месторождения, построить график PКОН [МПа]=f(t[годы]). Таблица 2 - Таблица исходных параметров Продолжение таблицы 2.
РЕШЕНИЕ Изменение давления для упругого режима в неограниченной законтурной области R < r ≤ ∞ при радиальной фильтрации воды описывается дифференциальным уравнением в частных производных: 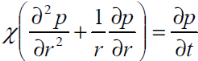 (1.9) (1.9)где: Известно частное решение уравнения (2.1), описывающее изменение давления в зависимости от мгновенного изменения объема жидкости в пласте:  (1.10) (1.10)где: С и А – константы интегрирования. С помощью интеграла Дюамеля можно показать, что при переменном во времени отборе воды qЗВ=αt.для 0 ≤ t≤ t1 решение имеет вид: 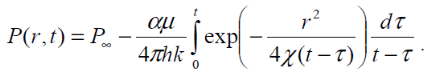 (1.11) (1.11)Для каждого следующего периода t1 < t≤ t2и t2 < t≤ t3в (1.13) будут появляться соответствующие интегралы, и окончательное решение примет вид: 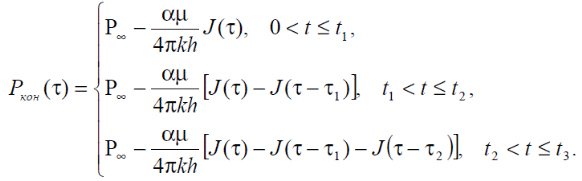 (1.12) (1.12)Здесь жидкости; Для произвольного τiинтеграл Дюамеля приближенно вычисляется по формуле:  (1.13) (1.13)Расчет представлен в таблице 1.3. Таблица 1.3 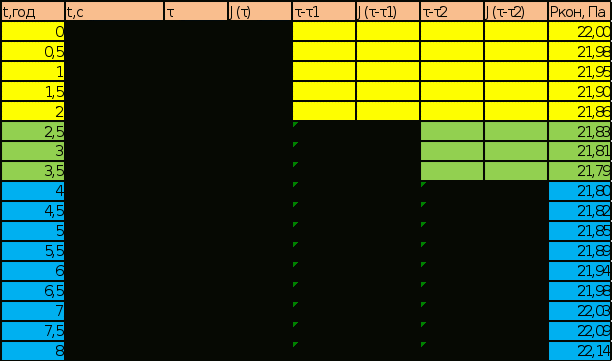 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
