Математика (автовосстановление). Решение Вычислим длины сторон ав Вычислим уравнения сторон ав и вс и их угловые коэффициенты

• Название: Решение Вычислим длины сторон ав Вычислим уравнения сторон ав и вс и их угловые коэффициенты
• Дата: 09.03.2023
• Размер: 66.43 Kb.
• Имя файла: Математика (автовосстановление).docx
• Тип: Решение; #976558

9. В задаче даны координаты вершин треугольника АВС. А (2;5) В (14;-4) С (18;18). Найти:

1. 
   Длины стороны АВ;
   
2. 
   Уравнение сторон АВ и ВС и их угловые коэффициенты;
   
3. 
   Уравнение высоты CD и ее длину;
   
4. 
   Уравнение медианы АЕ;
   
5. 
   Уравнение прямой, проходящей через точку С параллельно стороне АВ.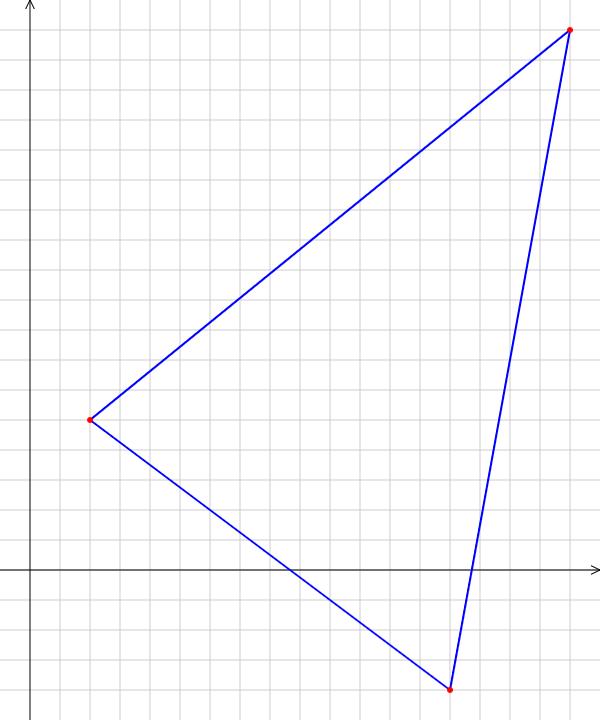
   

Решение:

1. 
   Вычислим длины сторон АВ: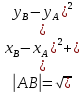
   

2. 
   Вычислим уравнения сторон АВ и ВС и их угловые коэффициенты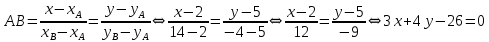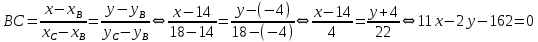
   

Угловые коэффициенты: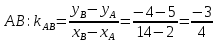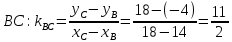

3. 
   Найдем уравнение высоты CD и ее длину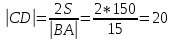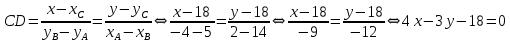
   

4. 
   Найдем уравнение медианы АЕ.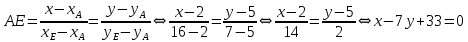
   

5. 
   Вычислим уравнение прямой, проходящей через точку С параллельно стороне АВ.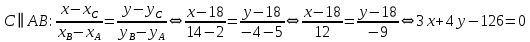
   

69. Найти производные и дифференциалы указанных функций

а)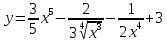

Решение: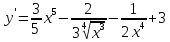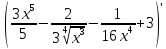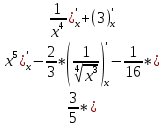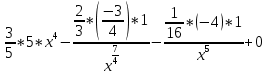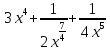










б)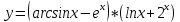
в)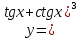
89. Найти неопределенные интегралы

а)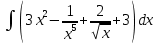
б)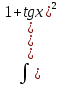
в)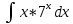
109. На ферме имеется 5 телочек и 4 бычка. Одна телочка и один бычок – близнецы. Какова вероятность, выбрать близнецов при случайном выборе телочки и бычка?
129. Доля поражения зерна вредителями в скрытой форме составляет 0,002. Найти вероятность, что из 500 семян 10 семян будут поражены вредителями.
149. В задаче задан закон распределения с.в.х. Найти:

1) математическое ожидание М(Х);

2) дисперсию D(Х);

3) среднее квадратическое отклонение σ

х	60	64	67	70
р	0,1	0,3	0,4	0,2

169. Масса выдавливаемых в пруду зеркальных карпов – случайная величина Х, распределенная по нормальному закону с математическим ожиданием 425 и средним квадратическим отклонением 30.

Найти:

а) вероятность того, что масса наудачу выловленного карпа будет заключена в пределах от 375 до 475;

б) вероятность того, что абсолютная величина отклонения X-d окажется меньше 60;

в) по правилу трех сигм найти наибольшую и наименьшую границы предполагаем массы.
189. Для средней урожайности пшеницы в каждом из двадцати совхозов района была определена урожайность на 100 га в каждом из них.

Для каждого совхоза найти:

1. 
   Величину, которую следует принять за среднюю урожайность на всем массиве;
   
2. 
   Величину, которую следует принять за среднее квадратическое отклонение урожайности на всем массиве;
   
3. 
   Доверительный интервал, в котором с вероятностью 0,95 заключена средняя урожайность на всем массиве.
   

10-12	12-14	14-16	16-18	18-20	20-22	22-24
4	8	15	21	25	13	14

Решение:

В качестве приближенного значения средней урожайности на всем массиве принимаем среднюю арифметическую данного распределения, то есть выборочную среднюю. За значение признака нужно принять середины интервалов. Получим: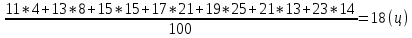



Среднеквадратическое отклонение: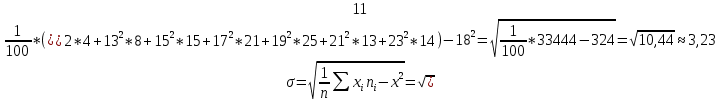