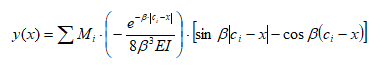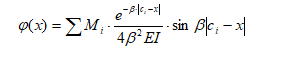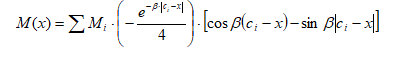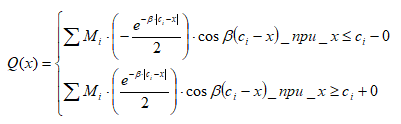Курсовая работа ППММ. Пояснительная записка. Курсовая работа По дисциплине Информатика (наименование учебной дисциплины, согласно учебному плану) Тема работы Метод начальных параметров при расчете балок на упругом основании
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
М  инистерство науки и высшего образования Российской Федерации инистерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего образования Санкт-Петербургский горный университет Кафедра информатики и компьютерных технологий Курсовая работа По дисциплине Информатика (наименование учебной дисциплины, согласно учебному плану) Тема работы Метод начальных параметров при расчете балок на упругом основании Выполнил: студент гр. НБ-19-2 Бадр М.А. (шифр группы) (подпись) (Ф.И.О.) Оценка: Дата: Проверил Руководитель работы: доцент Сибирев В.Н. (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2020 Министерство науки и высшего образования Российской Федерации  Федеральное государственное бюджетное образовательное учреждение высшего образования Санкт-Петербургский горный университет УТВЕРЖДАЮ Заведующий кафедрой Маховиков А.Б. (подпись) «»2020г. Кафедра информатики и информационных технологий КУРСОВАЯ РАБОТА По дисциплине Информатика (наименование учебной дисциплины, согласно учебному плану) ЗАДАНИЕ студенту группы НБ-19-2 Бадр М.А. (шифр группы) (Ф.И.О.) 1. Тема работы Решение базовых задач 2. Исходные данные к работе: Методом начальных параметров рассчитать стальную балку длиной L = 113 м, лежащую на упругом плотном грунте. Ширина постели b = 0,12 м. Балка нагружена сосредоточенной силой P = 92100 H, приложенной в точке b1=14 м. Механические параметры балки E=3200000000 Н/м2, I=0,2760 м4. 3. Содержаниепояснительной записки: Титульный лист, аннотация, оглавление; введение, разделы 1-2, заключение, список использованной литературы 4. Перечень графического материала: Рисунки, таблицы 5. Срок сдачи законченной работы 2020г. 6. Задание выдал (руководитель работы) Сибирев В.Н. (подпись) (Ф.И.О) 7. Задание принял к исполнению студент Бадр М.А. (подпись) (Ф.И.О) 8. Дата получения задания 2020г.  Аннотация В пояснительной записке приведен расчет балки на изгиб методом начальных параметров в табличном процессоре Microsoft Excel, вычислительной среде Mathcad и среде разработки Delphi. Пояснительная записка выполнена в текстовом редакторе Microsoft Word. Проект содержит пояснительную записку объемом 20 стр., вкл. 18 рис., библ. список из 5 наим. Annotation In the explanatory memorandum presents the calculation of the beam bending method of initial parameters in the spreadsheet application Microsoft Excel and environment Delphi. Explanatory note is made in the text editor Microsoft Word. The project contains an explanatory note displacement 20 pages, incl. 18 figures, 5 references. ОГЛАВЛЕНИЕ ВведениеНеобходимость использовать возможности компьютера появилась достаточно давно. Множество расчетов и работа с большими, а главное достаточно точными числа, обязывают использовать дополнительные программы для более точного решения задачи. Поэтому сейчас использовать компьютерные технологии не просто возможно, а необходимо. Это значительно повышает качество и уменьшает время выполнения работы. Компьютерные программы также позволяют практически мгновенно получить графическое изображение полученных результатов, например, в виде графиков, либо гистограмм. Это значительно повышает уровень восприятия информации. Кроме того, использование компьютерных программ уменьшает шанс совершения ошибки при расчете данных, а также позволяет практически мгновенно исправить допущенные ошибки. Напряжения, возникающие в разных сечениях балки, зависят от величины изгибающего момента и перерезывающей силы в соответствующих сечениях. При исследовании балок нужно знать величины M и Q в любом сечении. Изменение этих величин по всей длине балки удобнее всего представить графически. Линию, параллельную оси балки, принимают за ось абсцисс и строят два графика, ординаты которых изображают для каждого сечения балки соответствующие значения M и Q. Эти графики называют эпюрами изгибающих моментов и перерезывающих сил. Для построения эпюр используют различные методы: в частности, метод начальных параметров. Целью выполняемой работы является расчет стальною балки длиной L = 113 м, лежащую на упругом плотном грунте. Ширина постели b = 0,12 м. Балка нагружена сосредоточенной силой P = 92100 H, приложенной в точке b1=14 м. Механические параметры балки E=3200000000 Н/м2, I=0,2760 м4. Поскольку отношение β*L > 2π определяет тип балки, то необходимо высчитать произведение β*L. В данном случае оно равно 48,5. Поскольку 48,5 > 2π, то имеется длинная балка. 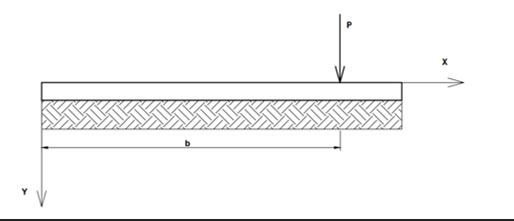 Схема балкиМетод начальных параметров при расчете балок на изгибВ тех случаях, когда нагрузка, действующая на балку, занимает незначительный по сравнению с длиной балки участок, достаточно удаленный от ее концов, балку можно считать бесконечно длинной. Критерием отнесения балки к длинной является выполнение неравенства 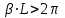 , где , где 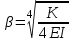 , , 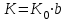 ( (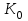 - коэффициент постели). В этом случае решение уравнения изгиба балки - коэффициент постели). В этом случае решение уравнения изгиба балки 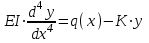 при приложении к ней сосредоточенной нагрузки при приложении к ней сосредоточенной нагрузки 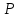 имеет вид: имеет вид:
Прогиб, угол поворота и момент симметричны относительно точки приложения силы, поперечная сила – кососимметрична. Применение аналитического решения к балке, нагруженной сосредоточенной силойРешение средствами табличного процессора Microsoft ExcelНачальные параметры определяются при помощи функций МОБР() и МУМНОЖ( ). Для наглядного представления строятся графики. 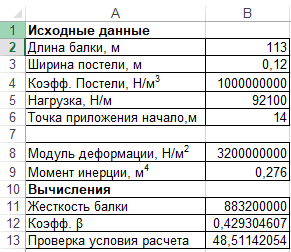 Начальные вычисления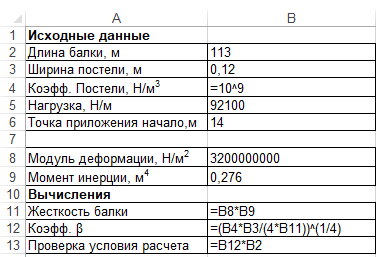 Начальные вычисления в виде отображения формул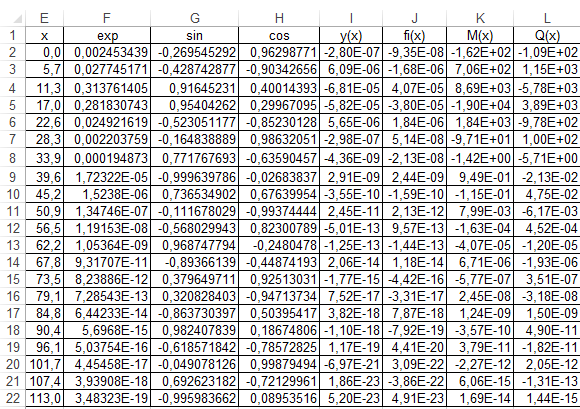 Вычисление фундаментальных функций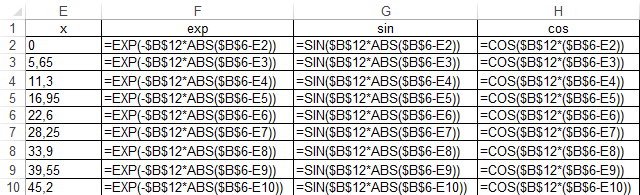 Вычисление фундаментальных функций и искомых величин в режиме отображения формул (часть 1)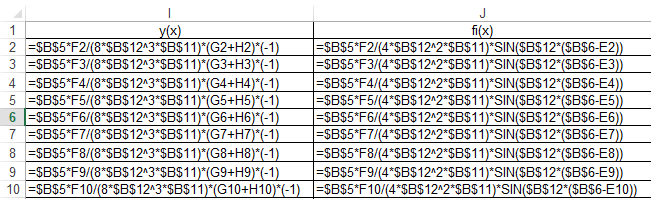 Вычисление фундаментальных функций и искомых величин в режиме отображения формул (часть 2)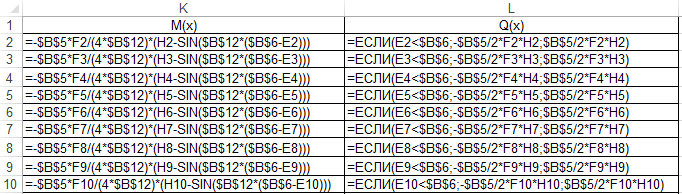 Вычисление фундаментальных функций и искомых величин в режимеПостроение эпюр: 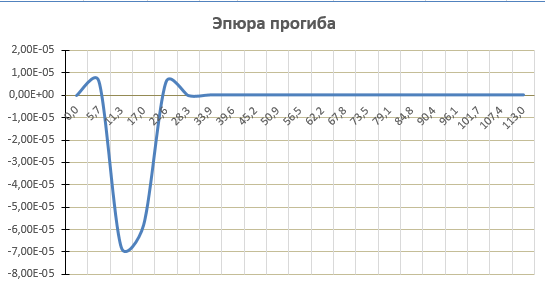 Эпюра прогиба балки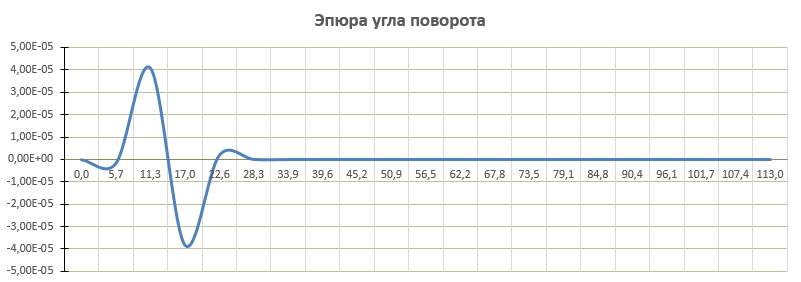 Эпюра угла поворота балки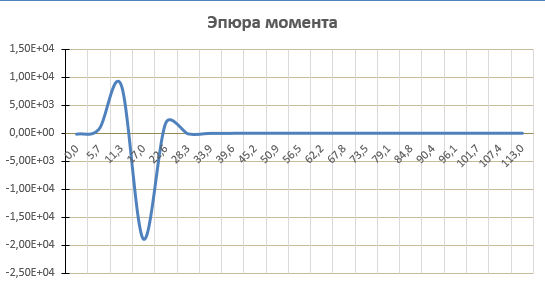 Эпюра изгибающего момента балки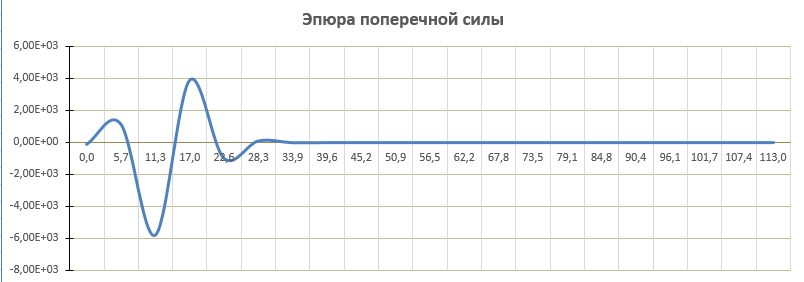 Эпюра поперечной силыРешение средствами пакета математических расчетов MathCADВычисление начальных параметров производится при помощи функции lsolve( ). Для наглядного представления строятся графики. 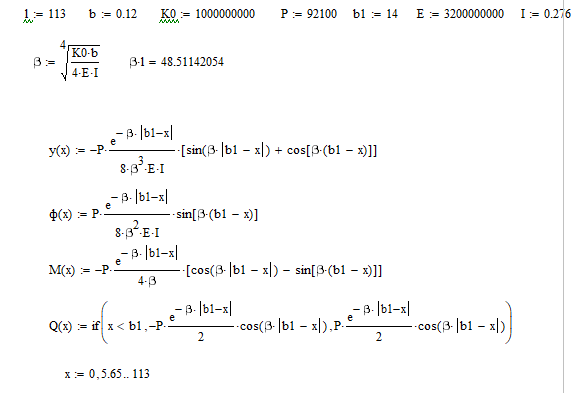 Вычисление начальных параметров и искомых величин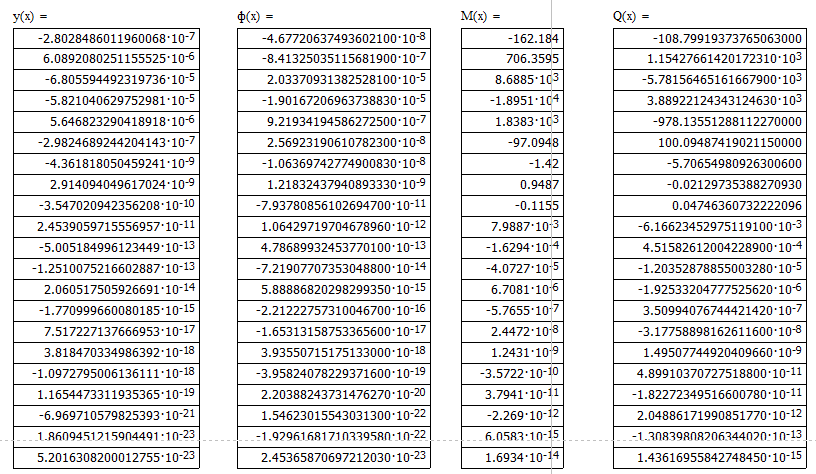 Результаты вычислений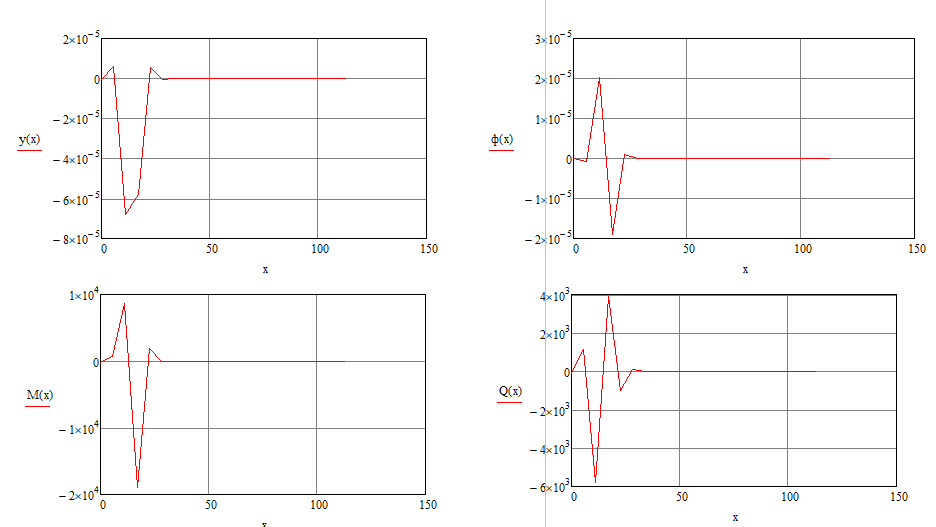 Эпюра вычисляемых величин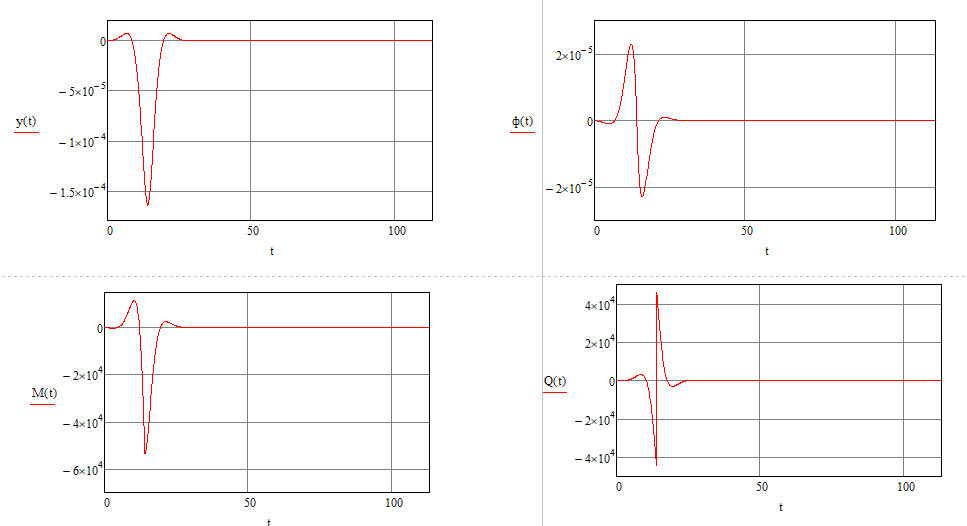 Эпюры, представленные в аналитическом виде.Решение задачи путем составления программы в среде создания WINDOWS-приложений DelphiДля лучшего понимания алгоритма действий для решения задачи, предлагаю рассмотреть блох-схему 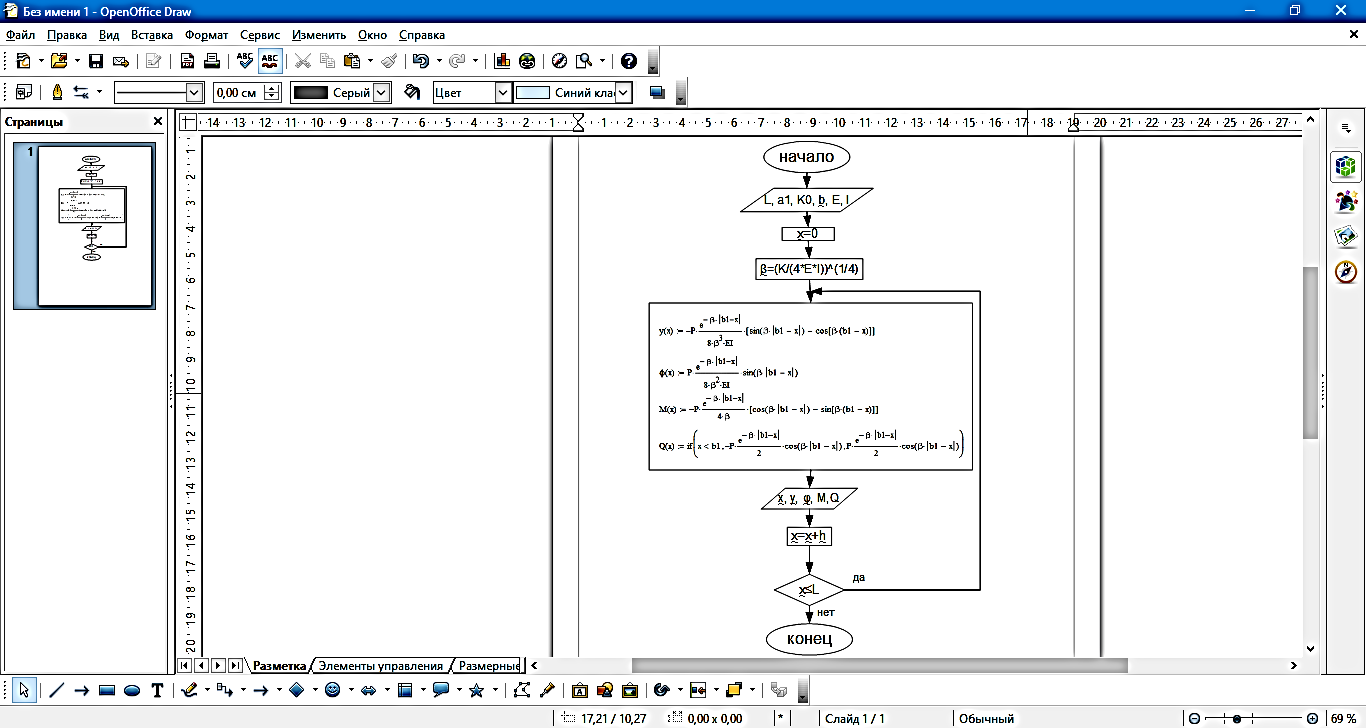 Блох-схема алгоритма решаемой задачиНиже описаны все переменные и массивы, использованные в программе: P, b1, L, b, K0, beta, E, I – переменные дробного типа, предназначенные для хранения исходных данных y, φ, M, Q- переменные дробного типа, предназначенные для хранения рассчитываемых значений x- переменная дробного типа, предназначенная для хранения значений коэффициентов Составили внешний вид программы, используя встроенные блоки Delphi: 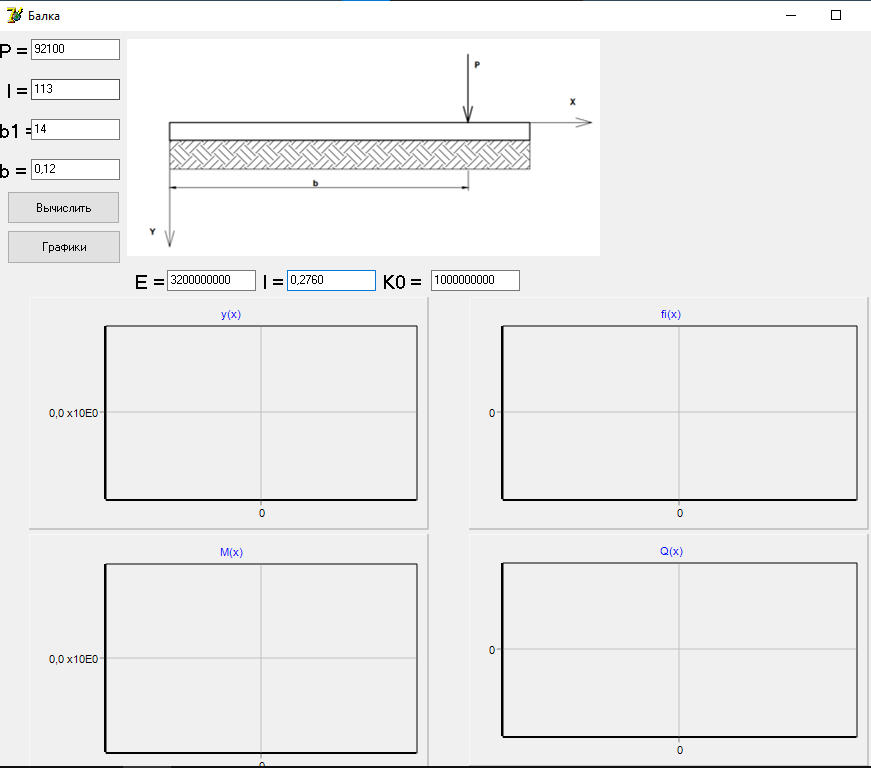 Внешний вид программы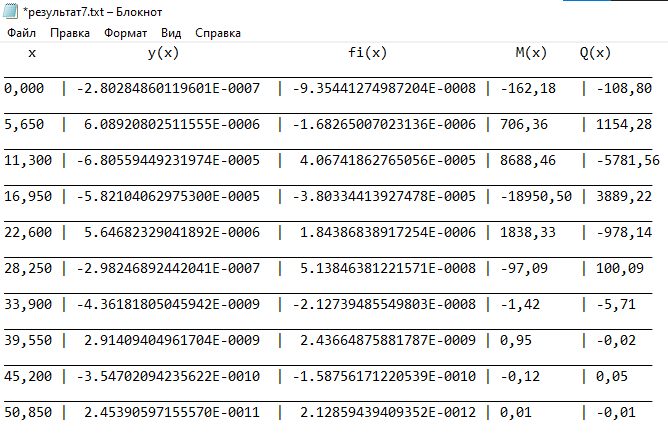 Результат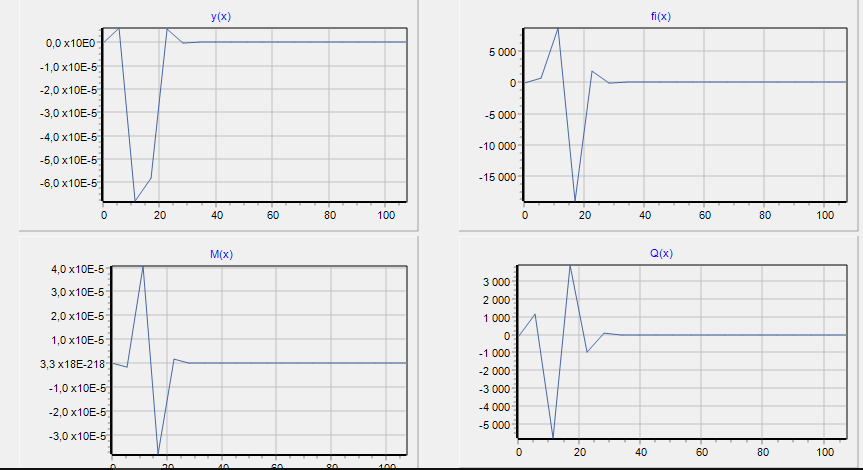 Полученные графикиКод программы: unit Unit1; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, ExtCtrls, jpeg, Math, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart, Vcl.Imaging.pngimage; type TForm1 = class(TForm) Edit1: TEdit; Edit2: TEdit; Button1: TButton; Label1: TLabel; Label2: TLabel; Image1: TImage; Edit3: TEdit; Label3: TLabel; Label5: TLabel; Edit5: TEdit; Label6: TLabel; Edit6: TEdit; Label7: TLabel; Edit7: TEdit; Edit8: TEdit; Label8: TLabel; Button2: TButton; Chart1: TChart; Chart2: TChart; Series2: TLineSeries; Series1: TLineSeries; Chart3: TChart; Series3: TLineSeries; Chart4: TChart; Series4: TLineSeries; procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); private { Private declarations } public { Public declarations } end; var Form1: TForm1; P,b1,l,b,K0,beta,E,I,v,v1,QX,MX,x:real; f:textfile; implementation {$R *.dfm} procedure TForm1.Button1Click(Sender: TObject); begin P:=strtofloat(Edit1.Text); l:=strtofloat(Edit2.Text); b1:=strtofloat(Edit3.Text); b:=strtofloat(Edit5.Text); E:=strtofloat(Edit6.Text); I:=strtofloat(Edit7.Text); K0:=strtofloat(Edit8.Text); beta:=power((K0*b/(4*E*I)),(1/4)); x:=0; Assignfile (f,'результат7.txt'); rewrite(f); Writeln(f,' x y(x) fi(x) M(x) Q(x)'); Writeln(f,'_________________________________________________________________________________'); while x<=l do begin If x begin v:=P*exp(-beta*abs(b1-x))/(8*power(beta,3)*E*I)*(sin(beta*abs(b1-x))+cos(beta*abs(b1-x)))*(-1); v1:=P*exp(-beta*abs(b1-x))/(4*sqr(beta)*E*I)*sin(beta*(b1-x)); MX:=-P*exp(-beta*abs(b1-x))/(4*beta)*(cos(beta*abs(b1-x))-sin(beta*(b1-x))); QX:=-P/2*exp(-beta*abs(b1-x))*cos(beta*abs(b1-x)); end else begin v:=P*exp(-beta*abs(b1-x))/(8*power(beta,3)*E*I)*(sin(beta*abs(b1-x))+cos(beta*abs(b1-x)))*(-1); v1:=P*exp(-beta*abs(b1-x))/(4*sqr(beta)*E*I)*sin(beta*(b1-x)); MX:=-P*exp(-beta*abs(b1-x))/(4*beta)*(cos(beta*abs(b1-x))-sin(beta*(b1-x))); QX:=P/2*exp(-beta*abs(b1-x))*cos(beta*abs(b1-x)); end; Writeln(f,FormatFloat('0.000',x),' | ', v,' | ',v1,' | ',FormatFloat('0.00',MX),' | ',FormatFloat('0.00',QX)); Writeln(f,'_________________________________________________________________________________'); x:=x+l/20; end; CloseFile(f); ShowMessage('Расчет произведен!'); x:=0; end; procedure TForm1.Button2Click(Sender: TObject); begin P:=strtofloat(Edit1.Text); l:=strtofloat(Edit2.Text); b1:=strtofloat(Edit3.Text); b:=strtofloat(Edit5.Text); E:=strtofloat(Edit6.Text); I:=strtofloat(Edit7.Text); K0:=strtofloat(Edit8.Text); beta:=power((K0*b/(4*E*I)),(1/4)); x:=0; Series1.Clear; Series2.Clear; Series3.Clear; Series4.Clear; while x<=(l) do begin If x begin v:=P*exp(-beta*abs(b1-x))/(8*power(beta,3)*E*I)*(sin(beta*abs(b1-x))+cos(beta*abs(b1-x)))*(-1); v1:=P*exp(-beta*abs(b1-x))/(4*sqr(beta)*E*I)*sin(beta*(b1-x)); MX:=-P*exp(-beta*abs(b1-x))/(4*beta)*(cos(beta*abs(b1-x))-sin(beta*(b1-x))); QX:=-P/2*exp(-beta*abs(b1-x))*cos(beta*abs(b1-x)); end else begin v:=P*exp(-beta*abs(b1-x))/(8*power(beta,3)*E*I)*(sin(beta*abs(b1-x))+cos(beta*abs(b1-x)))*(-1); v1:=P*exp(-beta*abs(b1-x))/(4*sqr(beta)*E*I)*sin(beta*(b1-x)); MX:=-P*exp(-beta*abs(b1-x))/(4*beta)*(cos(beta*abs(b1-x))-sin(beta*(b1-x))); QX:=P/2*exp(-beta*abs(b1-x))*cos(beta*abs(b1-x)); end; Series1.AddXY(x,v); Series2.AddXY(x,v1); Series3.AddXY(x,MX); Series4.AddXY(x,QX); x:=x+l/20; end end; end. ВыводыРасчет балки на изгиб можно производить с использованием компьютера в вычислительной части расчёта. Применение табличного процессора MS Excel, благодаря большому количеству встроенных функций, значительно ускоряет вычисления и позволяет не только производить расчёты на компьютере, но и получать графический вариант эпюр. Программа на языке программирования Delphi является реализацией цикла табулирования, типичной задачей курса информатики. При этом в MathCAD и Delphi достаточно изменить начальные условия, чтобы получить решения для большего количества данных, когда в то же время в MS Excel придется использовать операцию копирования формул, что не всегда удобно. Выполнение всех этих действий полностью подготовлено содержанием курса «Информатика», изученного в I и II семестрах. Список источниковПоловко А.М. MathCAD для студента / А.М. Половко, И.В. Ганичев. СПб.: БХВ-Петербург, 2006. 336 с. Леонтьев В. Самоучитель Word и Excel – все версии. М.: ОЛМА Медиа Групп, 2009. 256 с. В. К. Толстых Программирование в среде Delphi. Учеб.-метод. пособие для бакалавров инженерных и физических специальностей. – Донецк: ДонНУ, 2010. – 128 с. Правила оформления курсовых и квалификационных работ. Методические указания. /Онушкина И.О., Талалай П. Г. – СПб.: РИЦ горн. ин-т., 2005. 56 c. Степин П.А. Сопротивление материалов. М.: Недра, 1983. 303 с. |