криптография. Курсовая работа по дисциплине Криптография и безопасность компьютерных сетей На тему Математические основы и программная реализациясхемы разделения секрета на основе китайской теоремы об остатках

• Название: Курсовая работа по дисциплине Криптография и безопасность компьютерных сетей На тему Математические основы и программная реализациясхемы разделения секрета на основе китайской теоремы об остатках
• Анкор: криптография
• Дата: 17.06.2022
• Размер: 124.67 Kb.
• Имя файла: kursach_kripta (3).docx
• Тип: Курсовая; #600761

ФГБОУ ВО «Северо-Кавказский горно-металлургический институт (государственный технологический университет)»

Факультет: Информационных технологий и электронной техники

Кафедра: ИВТ

Курсовая работа

по дисциплине

«Криптография и безопасность компьютерных сетей»

На тему

«Математические основы и программная реализациясхемы разделения секрета на основе китайской теоремы об остатках»

Выполнил:студент гр. ИВб-18-2

Асламурзаев А.А.

Преподаватель: Калиниченко А.В.

Владикавказ 2021г.

Содержание

ВВЕДЕНИЕ 3

1.ОБЩИЙ РАЗДЕЛ 5

1.2 Основные определения 5

1.3 Схема разделения секрета 7

Совершенность и идеальность схемы разделения секрета 10

2. Специальный раздел 12

2.1Алгоритм работы программы 12

2.2Программный код и скриншоты 16

Заключение 20

Список использованной литературы 21

ВВЕДЕНИЕ

На протяжении всей истории человечество старалось скрыть определённую информацию от посторонних глаз. Поэтому не удивительно, что из этого желания возникла целая наука – криптография. Криптография -ровесница письменности. Эта наука прошла путь от папируса до компьютера и по возрасту старше египетских пирамид. Она в своем развитии прошла через этапы: криптография как искусство и криптография как ремесло к этапу криптография как наука.

Считается, что основы криптографии заложил Эней Тактик-один из самых ранних греческих авторов, писавший об искусстве войны. По-видимому, он был политическим деятелем и полководцем Аркадийского союза.

Попытки зашифровать данные делали ещё в древней Индии и Месопотамии. Нельзя сказать, что эти попытки были удачными, так как основой криптографии является математика и в те времена математический аппарат не был еще развит настолько, чтобы осуществлять такие нетривиальные задачи. Криптография всегда развивались в тесном взаимодействии с математикой. Эти науки взаимно дополняли и обогащали друг друга. Математический аппарат продолжает оставаться основным в криптографии. Ведь не случайно в многовековую историю криптографии вписано много имен видных математиков.

Шифры активно использовали древние цивилизации Вавилона, Египта, Греции, Рима, Китая и Индии.Существовали три основных способа защиты информации. Один из них предполагал защиту ее чисто силовыми методами: охрана документа - носителя информации - физическими лицами, передача его специальным курьером и т.д.

Второй способ получил название "стеганография" (латино-греческое сочетание слов, означающих в совокупности "тайнопись"). Он заключался в сокрытии самого факта наличия информации. В данном случае использовались так называемые симпатические чернила. При соответствующем "проявлении" бумаги текст становится видимым. Один из примеров сокрытия информации приведен в трудах древнегреческого историка Геродота. На голове раба, которая брилась наголо, записывалось нужное сообщение. И когда волосы его достаточно отрастали, раба отправляли к адресату, который снова брил его голову и считывал полученное сообщение.

Третий способ защиты информации заключался в преобразовании смыслового текста в некий набор хаотических знаков (или букв алфавита). Получатель данного донесения имел возможность преобразовать его в то же самое осмысленное сообщение, если обладал ключом к его построению. Этот способ защиты информации называется криптографическим. Криптография - слово греческое и в переводе означает "тайнопись". Первая надёжная система защиты была разработана в Древнем Китае. В этом шифре использовались элементы китайского алфавита, которые символизировали определенную мысль, которая в свою очередь шифровала истинный смысл сообщения.

1. ОБЩИЙ РАЗДЕЛ

1.2 Основные определения

Шифр – совокупность заранее оговоренных способов преобразования исходного секретного сообщения с целью его защиты.

Исходные сообщения обычно называют открытыми текстами.

Символ - это любой знак, в том числе буква, цифра или знак препинания.

Алфавит - конечное множество используемых для кодирования информации символов. Например, русский алфавит содержит 33 буквы от А до Я. Однако этих тридцати трех знаков обычно бывает недостаточно для записи сообщений, поэтому их дополняют символом пробела, точкой, запятой и другими знаками. Алфавит арабских цифр – это символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Этот алфавитсодержит 10 знаков и с его помощью можно записать любое натуральное число. Любое сообщение может быть записано также с помощью двоичного алфавита, то есть с использованием только нулей и единиц.

Сообщение, полученное после преобразования с использованием любого шифра, называется шифрованным сообщением(закрытым текстом, криптограммой).

Преобразование открытого текста в криптограмму называется зашифрованием. Обратное действие называется расшифрованием.

Ключ – информация, необходимая для шифрования и расшифрования сообщений.

Система шифрования или шифр-система, – это любая система, которую можно использовать для обратимого изменения текста сообщения с целью сделать его непонятным для всех, кроме тех, кому оно предназначено.

Криптостойкостью называется характеристика шифра, определяющая его стойкость к дешифрованию без знания ключа (т.е. способность противостоять криптоанализу).

С учетом всех сделанных определений можно дать определение науке "криптография". Криптографияизучает построение и использование систем шифрования, в том числе их стойкость, слабости и степень уязвимости относительно различных методов вскрытия.

 Шифрование с закрытым ключом (шифрование с секретным ключом или симметричное шифрование) используется человеком уже довольно долгое время. Для шифрования и расшифрования данных в этих методах используется один и тот же ключ, который обе стороны стараются хранить в секрете от противника.

Шифрование с открытым ключом(асимметричное шифрование) стало использоваться для криптографического закрытия информации лишь во второй половине ХХ века. В эту группу относятся методы шифрования, в которых для шифрования и расшифрования данных используются два разных ключа. При этом один из ключей (открытый ключ) может передаватьсяпооткрытому (незащищенному) каналу связи.

Электронной (цифровой) подписью называется обычно присоединяемый к сообщению блок данных, полученный с использованием криптографического преобразования. Электронная подпись позволяет при получении текста другим пользователем проверить авторство и подлинность сообщения.

Криптографическая система защиты информации – система защиты информации, в которой используются криптографические методы для шифрования данных.

1.3 Схема разделения секрета

Схема разделения секрета представляет собой схему предварительного распределения ключей между уполномоченными группами пользователей, в которой ключ заранее определен и одинаков для каждой уполномоченной группы. При этом каждый пользователь получает свою долю или “часть секрета”. Схема включает два протокола: протокол формирования долей (разделения секрета) и распределения их между пользователями и протокол восстановления секрета группой пользователей. Схема должна позволять восстанавливать ключ только тем группам пользователей, которые имеют на это полномочия, и никакая другая группа не должна иметь возможности для восстановления ключа или получения о нем какой-либо информации.

Основное назначение схемы разделения секрета — защита ключа от потери. Обычно для защиты от потери делают несколько копий ключа. С возрастанием числа копий ключа возрастает вероятность его компрометации. Если число копий мало, то велик риск потери ключа. Поэтому лучше “разделить” ключ между несколькими лицами так, чтобы допускалась возможность восстановления ключа при различных обстоятельствах несколькими уполномоченными группами с заранее оговоренным составом участников. Тем самым исключается риск безвозвратной потери ключа.

Еще одно положительное качество схем разделения секрета заключается в разделении ответственности за принятие решения, которое автоматически вводится при определении состава уполномоченных групп. Такая коллективная ответственность нужна для многих приложений, включая принятие важных решений, касающихся применения систем оружия, подписания корпоративных чеков или допуска к банковскому хранилищу.

В простейшем случае, когда имеется только одна группа, состоящая из t пользователей, уполномоченная формировать ключ, схему разделения секрета можно построить следующим образом. Предположим, к примеру, что ключ представляет собой двоичный вектор s длины m. Выберем случайным образом t векторов s₁…s_t, так, чтобы их сумма совпадала с вектором s и распределим их между пользователями. Теперь, собравшись вместе, они могут легко восстановить значение ключа, в то время как никакая группа, состоящая из меньшего числа пользователей, не сможет этого сделать. Действительно, в данном случае отсутствие хотя бы одной доли приводит к полной неопределенности относительно значения секрета, поскольку для каждого значения искомого секрета найдется возможный вариант значения отсутствующей доли.

Важно отметить, что если бы в предыдущем примере просто разбить вектор на t частей, то такая схема не могла быть схемой разделения секрета, так как знание любой доли давало бы частичную информацию о секретеs.

Протоколы разделения секрета призваны решить проблему хранения информации так, чтобы те группы людей, которым позволено знать секрет, могли бы его восстановить, а те группы, которым секрет знать не позволено, восстановить его не смогли даже путем перебора.

В протоколе разделения секрета имеются n участников (абонентов) P₁,P₂,...,P_nи один выделенный участник D, называемый дилером (раздающим). Пусть через P ={P₁,P₂,...,P_n}обозначено множество всех абонентов. Введем следующую терминологию:

• 
  группа доступа (разрешенная группа) – непустое подмножество A участников множества P, которые, собравшись вместе, имеют право восстановить секрет;
  
• 
  структура доступаГ будем называть непустое множество всех групп доступа.
  

Далее будем полагать, что любой участник P₁,P₂,...,P_nвходит хотя бы в одну группу доступа, иначе присутствие его присутствие бессмысленно. Также считаем, что Г замкнуто, то есть если A⊂B ⊂P и A⊂Г, то B⊂Г. Действительно, если абоненты P₁,P₂,...,P_kмогут совместно восстановить секрет, то, если к ним присоединятся дополнительные участники P_k+1,P_k+2,..., то получившаяся группа тем более сможет восстановить секрет.

Протокол разделения секрета состоит из двух основных фаз.

1. 
   Разделение секрета – фаза раздачи, когда дилер, знающий секрет M, генерирует n долей m₁, m₂,...,m_nсекрета и выдает каждому участнику его долю по защищенному каналу связи. Раздачу нужно организовать так, чтобы разрешенные группы участников, собравшись вместе, могли однозначно восстановить секрет, а неразрешенные – не могли.
   
2. 
   Фаза восстановлениясекрета, когда какая–либо группа из структуры доступа Г объединяет свои доли секретов и получает секрет.
   

Сформулируем китайскую теорему об остатках.

Система сравнений вида:



где m₁, m₂,...,m_k– попарно простые числа, имеет единственное решение





Схема разделения секрета на основе китайской теоремы об остатках выглядит следующим образом:

Пусть N – общий секрет.

1) Фаза раздачи секрета.

Дилер выбирает p₁, p₂,..., p_n– различные простые числа. Доля секрета, выдаваемая i -му участнику схемы, есть число x_i≡ N modp_i. При выборе чисел p₁, p₂,..., p_nдилер должен проверить два условия:

• 
  произведение, составленное из k любых этих чисел, должно быть больше, чем N. Это достигается, когда для всех i выполняется ;
  
• 
  чтобы гарантировать, что k−1 участников не могут восстановить секрет без k -го участника, необходимо, чтобы для всех i.
  

2) Фаза восстановления секрета.

Собравшись вместе, k участников составляют и решают систему сравнений относительно неизвестного N: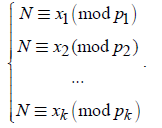



Решение системы дает общий секрет N.

Совершенность и идеальность схемы разделения секрета

Пусть M – множество секретов, которые можно разделить поданной схеме. Схема разделения секрета называется совершенной,если любая группа участников, не имеющая доступа к восстановлениюсекрета, объединив свои доли секрета, не может отвергнуть какневозможный ни один из секретов множества M.

Схема разделения секрета называется идеальной, если все частисекрета и сам секрет одинакового размера и могут равновероятнопринимать любое значение из допустимых значений в данной схеме.

Схема на основе китайской теоремы об остатках не являетсясовершенной, так как участник, зная свою долю (x_i,p_i) , можетисключить из рассмотрения все секреты, для которых остаток отделения на p_iне равен x_i.

Пороговой схемой разделения секрета(k,n; k ≤n) называется такая схема, в которой секрет разделяется между n участниками, причем разрешенной группой является любая группа из не менее, чем k участников.

Пусть M – секрет, который следует разделить между nучастниками, а структура доступа состоит из одного множестваГ= P ={P₁,P₂,...,P_n}, т.е. восстановить секрет могут только всеучастники схемы, соединив свои доли. Выбирается модуль d >M.

Фаза раздачи секрета.

Дилер выбирает случайные числа S₁,S₂,...,S_n−1 из Z_dивычисляется числоS_n= M −S₁−S₂−...−S_n−1(modd)

Поскольку S₁,S₂,...,S_n−1 – случайные числа, то и S_nтоже будетслучайным числом. Затем доли секрета S₁,S₂,...,S_nдилер рассылаютсяучастникам: i -ый участник получает число S_i.

Фаза восстановления секрета.

Участники P₁,P₂,...,P_nобъединяют свои доли секрета и вычисляютM= S₁+S₂+...+S_n−1+S_n(modd).

Описанная схема является совершенной и идеальной.

Совершенность следует из того, что, объединив менее чем n долейсекрета, участники вычислят случайное число, которое не даст никакойинформации о M. Идеальность очевидна, поскольку каждый участникполучает долю секрета, размер которой равен размеру самого секрета.

Ранее мы рассмотрели схемы разделения секрета как протокол, вкотором участники доверяют раздающему на фазе разделения секрета,и доверяют друг другу на фазе восстановления секрета. Рассмотримтеперь случай, когда некоторые участники протокола могут оказатьсяпротивниками. Задачей протокола разделения секрета в таком случаеявляется защита честных участников от мошенничества противников.Конечно, если противником является раздающий, он может простосаботировать выполнение протокола, и невозможно предложитькриптографическую защиту от такого рода действий. Но саботажпротокола мгновенно выявляется и может быть пресечен другимиметодами. Честные участники в таком случае доверят разделениесекретов другим, честным, дилерам.

Для защиты же от более хитрых действий противника возниклаидеяпроверяемого разделения секрета.Идея такова: на этапе разделения секрета дилер публикует секретв зашифрованном виде так, чтобы, пользуясь этой информацией, никтоне мог восстановить секрет, но, чтобы каждый абонент, используя своюдолю секрета, мог проверить, с того ли секрета была получена эта доля.

Кроме дилера, злоумышленниками могут являться некоторые изабонентов. Нечестные участники могут попытаться помешатьвосстановлению секрета, посылая не свои доли секрета, а какие-тодругие значения. От протокола требуется, чтобы все честные участники,если их не менее t, всегда правильно восстанавливали значениесекретаM.

2. Специальный раздел

2.1Алгоритм работы программы

Разделение секрета

Первым делом нужно объявить 3 коллекции однотипных объектов:

1)В первой будем хранить простые элементы.

2)Во второй храним доли секрета, выдаваемые каждому участнику.

3)В третьей будут храниться простые элементы, удовлетворяющие требуемым условиям для расчетов.

privatevoid button1_Click(object sender, EventArgs e)

{

Random R = newRandom();

List prost = newList();

List p = newList();

List x = newList();

int S = Convert.ToInt32(textBox1.Text);

int k = Convert.ToInt32(textBox2.Text);

Проверяем, есть ли среди наших простых чисел интервал длиной, превышающей количество участников, участвовавших в разделении секрета:

if (a == 0) { a = 1; };

bool f = false;

for (int q = a+1; q < b; q++ ) {

for (inti = 2; i< q; i++ )

{

if (q % i == 0) { f = true; break; };

};

if (f == false) { prost.Add(q); };

f = false;

};

if (prost.Count< k) { MessageBox.Show("натакоеколичествочастейнельзяразделитьсекрет"); return; };

Выбираем из массива простых чисел некоторое количество, выбранных случайным образом:

intvr = 0;

for (inti = 0; i< k; i++) {

vr=prost[R.Next(0,prost.Count-1)];

p.Add(vr);

prost.Remove(vr);

};

Дилер выбирает p₁,p₂,...,p_n– различные простые числа. Доля секрета,выдаваемаяi-му участнику схемы, есть число x_i=(Nmodp_i):

for (inti = 0; i< k; i++ ) {

vr = S % p[i];

x.Add(vr); //доля секрета, выдаваемая каждому участнику

};

Простые числа необходимо выбирать их интервала :p_i<< 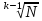для всех i:

if (k == 2) {

a = (int)Math.Pow(S, 1.0 / k);

b = Math.Sqrt(S);

}

elseif (k > 2)

{

a = (int)Math.Pow(S, 1.0 / k);

k--;

b = (int)Math.Pow(S, 1.0 / k);

k++;

};

Тестируем программу: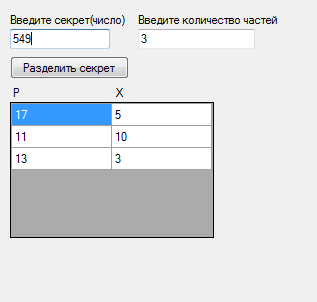



Программа корректно отображает взаимно простые числа и доли секрета, приходящихся на каждую из них. Если вдруг не удалось сгенерировать достаточную последовательность взаимно простых чисел для вводимого количества участников, программа даст об этом знать: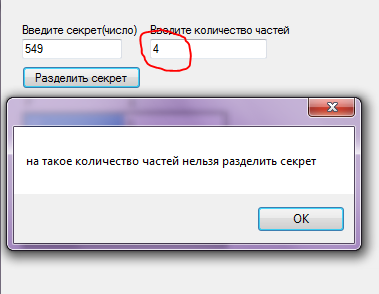



Фаза восстановления секрета

Собравшись вместе,k участников составляют и решают систему сравнений относительно неизвестного N.

Для этого перенесем данные, полученные в первой части программы:



Создадим новые коллекции однотипных элементов:

privatevoid button3_Click(object sender, EventArgs e)

{

int k = Convert.ToInt32(textBox3.Text);

List p = newList();

List x = newList();

List d = newList();

Listd_obr = newList();

Осуществляем проверку: соответствует ли количество введенных данных количеству частей разделенного секрета?

for (inti = 0; i< k; i++)

{

for (int j = 0; j < 2; j++)

{

if (dataGridView2.Rows[i].Cells[j].Value.ToString() == "")

{

MessageBox.Show("однаизячеекпустая"); return;

};

};

};

Запишемвнихсодержимое:

for (inti = 0; i< k; i++)

{

p.Add(Convert.ToInt32(dataGridView2.Rows[i].Cells[0].Value.ToString()));

};

for (inti = 0; i< k; i++)

{

x.Add(Convert.ToInt32(dataGridView2.Rows[i].Cells[1].Value.ToString()));

};

Соберем разделенный на части секрет в единый ключ согласно китайской теореме об остатках:

int D = 1;

for (inti = 0; i


D *= p[i];

};

for (inti = 0; i


{

d.Add( D/p[i]);

};

for (inti = 0; i
{

for (int q = 1; ; q++) {

if ((d[i] * q) % p[i] == 1) { d_obr.Add(q); break; };

};

};

intvr = 0;

for (inti = 0; i
{

vr += (x[i] * d[i] * d_obr[i]);

};

int S = vr % D;

Убедимся в том, что программа работает корректно и действительно безошибочно собирает ключ из его частей: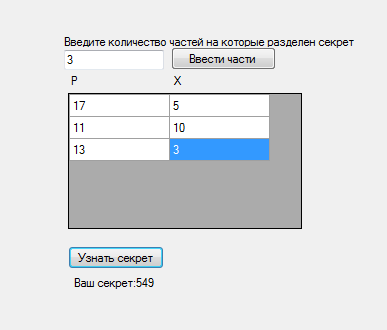



2.2Программный код и скриншоты

Using System;

Using System.Collections.Generic;

Using System.ComponentModel;

Using System.Data;

Using System.Drawing;

Using System.Linq;

Using System.Text;

Using System.Windows.Forms;
namespace WindowsFormsApplication1

{

publicpartialclassForm1 :Form

{

public Form1()

{

Initialize Component();

}
Private void button1_Click(object sender, EventArgs e)

{

Random R = new Random();

List prost = new List();

List p = new List();

List x = newL ist();

int S = Convert.ToInt32(textBox1.Text);

int k = Convert.ToInt32(textBox2.Text);

int a = 0 ;

double b=0;

if (k == 1) { MessageBox.Show("частей слишком мало"); return; };

if (k == 2) {

a = (int) Math.Pow(S, 1.0 / k);

b = Math.Sqrt(S);

}

elseif (k > 2)

{

a = (int)Math.Pow(S, 1.0 / k);

k--;

b = (int)Math.Pow(S, 1.0 / k);

k++;

};

if (a == 0) { a = 1; };

bool f = false;

for (int q = a+1; q < b; q++ ) {

for (int i = 2; i< q; i++ )

{

if (q % i == 0) { f = true; break; };

};

if (f == false) { prost.Add(q); };

f = false;

};

if (prost.Count< k) { MessageBox.Show("натакоеколичествочастейнельзяразделитьсекрет"); return; };

int vr = 0;

for (int i = 0; i< k; i++) {

vr=prost[R.Next(0,prost.Count-1)];

p.Add(vr);

prost.Remove(vr);

};

for (inti = 0; i< k; i++ ) {

vr = S % p[i];

x.Add(vr); //доля секрета, выдаваемая каждому участнику

};

dataGridView1.RowCount = k;

dataGridView1.ColumnCount = 2;

for (int i = 0; i< k; i++) {

dataGridView1.Rows[i].Cells[0].Value = p[i];

dataGridView1.Rows[i].Cells[1].Value = x[i];

};

}
Private void button2_Click(object sender, EventArgs e)

{

int k = Convert.ToInt32(textBox3.Text);

dataGridView2.RowCount = k;

dataGridView2.ColumnCount = 2;

for (int i = 0; i< k; i++)

{

for (int j = 0; j < 2; j++)

{

dataGridView2.Rows[i].Cells[j].Value = "";

};

};

}
Private void button3_Click(object sender, EventArgs e)

{

int k = Convert.ToInt32(textBox3.Text);

List p = new List();

List x = new List();

List d = new List();

Listd_obr = new List();

for (int i = 0; i< k; i++)

{

for (int j = 0; j < 2; j++)

{

if (dataGridView2.Rows[i].Cells[j].Value.ToString() == "")

{

MessageBox.Show("одна из ячеек пустая"); return;

};

};

};

for (int i = 0; i< k; i++)

{

p.Add(Convert.ToInt32(dataGridView2.Rows[i].Cells[0].Value.ToString()));

};

for (int i = 0; i< k; i++)

{

x.Add(Convert.ToInt32(dataGridView2.Rows[i].Cells[1].Value.ToString()));

};

int D = 1;

for (int i = 0; i


D *= p[i];

};

for (int i = 0; i


{

d.Add( D/p[i]);

};

for (int i = 0; i
{

for (int q = 1; ; q++) {

if ((d[i] * q) % p[i] == 1) { d_obr.Add(q); break; };

};

};

Int vr = 0;

for (int i = 0; i
{

vr += (x[i] * d[i] * d_obr[i]);

};

int S = vr % D;

label6.Text = "Ваш секрет:" + S.ToString();

}

}

}

Заключение

В ходе выполнения курсовой работы были изучены математические основы и программная реализация схемы разделения секрета на основе китайской теоремы об остатках.

Список использованной литературы

1. 
   КоутинхоС. Введение в теорию чисел. АлгритмRSA. Постмаркет, Москва, 2001 г.
   
2. 
   Шнайер Б. 3.7. Разделение секрета // Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = AppliedCryptography. Protocols, AlgorithmsandSourceCodein C. — М.: Триумф, 2002.
   
3. 
   Алферов А. П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. – Основы криптографии, Гелиос АРВ, Москва, 2002 г.
   
4. 
   Ященко В.В. - Введение в криптографию, МЦНМО, Москва, 2012 г.
   
5. 
   Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн - Алгоритмы: построение и анализ, Вильямс, 2009 г.