курсовая работа по криптографии. Курсовая работа по дисциплине Криптография
 Скачать 151.58 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ «СЕВЕРО-КАВКАЗСКИЙ ГОРНО-МЕТАЛЛУРГИЧЕСКИЙ ИНСТИТУТ» (ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ) Факультет: Информационных технологий и электронной техники Кафедра: Информатики и вычислительной техники Курсовая работа по дисциплине «Криптография» на тему «Математические основы и программная реализация: а) алгоритма разложения на множители путем деления методом проб; б) алгоритма Ферма разложения на множители.» Выполнил: студент гр. ИВб18-2 Джусоев Г.Р. Преподаватель: Калиниченко А.В. Оценка при защите: __________________________ __________________________ (подпись) «____»_______________20__г. Владикавказ 2021 Содержание Введение………………………………………………………………….. 3 1.Общий раздел………………………………………………………….…. 5 1.1.Описание предметной области рассматриваемого объекта………. 5 1.2. Постановка задачи…………………………………………..……….. 7 2. Специальный раздел…………………………………………………….. 9 2.1 Анализ требований к программному обеспечению……………… 9 Пример разложение на множители…………………………………… 12 2.2.Инструкция пользователя………………………………………….. 15 Заключение………………………………………………………………… 16 Список литературы………………………………………………...…….… 17 Приложения ………………………………………………………….……..18 Введение Термин «информационная безопасность» является одним из основных понятий и включает в себя много компонентов, таких как: процесс, передача, хранение или изменение информации. Для слаженной работы всех перечисленных компонентов необходимы подходящие технологии и системы безопасности, отвечающие потребностям и требованиям безопасной работы. Многие системы безопасности (например, протокола безопасности, алгоритмы или приложения) были разработаны на основе стандартов, которые в основном были предложены известными организациями (IAB, IETF и т. д.), чтобы обеспечить совместную и слаженную работу в функционировании таких систем и реализовать наши потребности в области безопасности в использовании информационных технологий. Потребность в безопасности и желание ее обеспечить не могут быть реализованы с помощью только одного механизма, однако мы можем отметить, что в основе многих механизмов безопасности лежит основная наука, называемая криптографией (наукой о шифровании и дешифровании данных). Шифрование позволяет пользователям безопасно хранить конфиденциальную информацию или передавать ее через небезопасные сети, так что она не может быть прочитана никем, кроме предполагаемого получателя. С помощью такого мощного инструмента как шифрование мы получаем конфиденциальность, подлинность, целостность и ограниченный доступ к данным. В криптографии различают частные ключевые криптографические системы и ключевые криптографические системы с общественностью. Секретный ключ криптографии, также известный как секретный ключ или симметричный ключ шифрования, имеет давнюю историю, и основан он на использовании одного ключа для шифрования и дешифрования. Многие развитые современные частные ключевые криптографические системы основаны на Feistel шифре (например, национальный стандарт шифрования США (DES), шифр (стандарт) DES с трёхкратным шифрованием (3DES), новый национальный стандарт шифрования США (AES), международный алгоритм шифрования данных (IDEA), Blowfish, RC5, CAST и т. д. В 1976 г. Диффи и Хеллман опубликовали документ, описывающий новую концепцию с открытым ключом, основанную на использовании двух ключей (открытого и закрытого). С помощью новой концепции мы можем решать многие проблемы (например, ключевую проблему обмена) в криптографии. С тех пор было изобретено много систем открытых ключей шифрования (например, RSA, ElGamal, обмена ключами Диффи-Хеллмана, эллиптических кривых и т. д.). Безопасность баз данных, основанная на использовании открытого ключа криптосистемы, обнаруживает трудности некоторых математических задач теории чисел (например, проблему дискретного логарифма над конечными полями и эллиптическими кривыми, задачи факторизации целых чисел или Диффи-Хеллмана и т. д.). Протокол Диффи-Хеллмана отлично противостоит пассивному нападению, но в случае реализации атаки «человек в центре» он не устоит. Схема Эль-Гамаля была предложена Тахером Эль-Гамалем в 1984 году. Эль-Гамаль разработал один из вариантов алгоритма Диффи-Хеллмана. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для шифрования и для обеспечения аутентификации. В отличие от RSA алгоритм Эль-Гамаля не был запатентован и, поэтому, стал более дешевой альтернативой, так как не требовалась оплата взносов за лицензию. Считается, что алгоритм попадает под действие патента Диффи-Хеллмана. Алгоритм Эль-Гамаля нашел применение в нашумевшей системе Pretty good privacy (PGP), где с помощью него осуществляется управление ключами. Использовался алгоритм цифровой подписи DSA, разработанный NIST (Национальный институт стандартов и технологий) и являющийся частью стандарта DSS (Национальный стандарт ЭЦП США). 1.Общий раздел1.1. Описание предметной области рассматриваемого объектаИсторически первыми появились симметричные криптографические системы. В симметричной криптосистеме шифрования используется один и тот же ключ для зашифровывания и расшифровывания информации. Это означает, что любой, кто имеет доступ к ключу шифрования, может расшифровать сообщение. Соответственно с целью предотвращения несанкционированного раскрытия зашифрованной информации все ключи шифрования в симметричных криптосистемах должны держаться в секрете. Именно поэтому симметричные криптосистемы называют криптосистемами с секретным ключом — ключ шифрования должен быть доступен только тем, кому предназначено сообщение. Данные криптосистемы характеризуются наиболее высокой скоростью шифрования, и с их помощью обеспечиваются как конфиденциальность и подлинность, так и целостность передаваемой информации. Асимметричные криптографические системы были разработаны в 1970-х гг. Принципиальное отличие асимметричной криптосистемы от криптосистемы симметричного шифрования состоит в том, что для шифрования информации и ее последующего расшифровывания используются различные ключи: Открытыйключ К используется для шифрования информации, вычисляется из секретного ключа К; секретный ключ к используется для расшифровывания информации, зашифрованной с помощью парного ему открытого ключа К. Эти ключи различаются таким образом, что с помощью вычислений нельзя вывести секретный ключ к из открытого ключа К. Поэтому открытый ключ К может свободно передаваться по каналам связи. Для криптографического закрытия и последующего расшифровывания передаваемой информации используются открытый и секретный ключи получателя В сообщения. В качестве ключа зашифровывания должен использоваться открытый ключ получателя, а в качестве ключа расшифровывания — его секретный ключ. Чтобы исключить работу с системой незаконных пользователей, необходима процедура распознавания системой каждого законного пользователя. Для этого в защищенном месте система обязана хранить информацию, по которой можно опознать пользователя, а пользователь обязан себя идентифицировать, т.е. указать идентификатор, присвоенный ему в данной системе. Получив идентификатор, система проводит его аутентификацию, т.е. проверяет его подлинность – принадлежность множеству идентификаторов. Аутентификация субъекта может осуществляться с использованием как симметричных, так и несимметричных криптоалгоритмов. В системах с большим числом пользователей применение симметричных методов требует введения в сеанс связи доверенной стороны, с которой разделяют секретные ключи все пользователи системы. Использование криптосистем с открытым ключом позволяет отказаться от серверов аутентификации, однако в системе должен существовать сервер, выдающий сертификаты на используемые субъектами взаимодействия открытые ключи. Сертификатом принято называть электронный документ, удостоверяющий принадлежность данного открытого ключа данному субъекту, иначе говоря, аутентичность ключа. 1.2. Постановка задачи Алгоритм разложения путем деления методом проб Ввод: натуральное число n Вывод: натуральное число f> 1 - наименьший простой делитель числа n или сообщение о том, что n простое. Шаг 1. Положить F=2 Шаг 2. Если n/F целое, то сообщить: “F является делителем числа n” и завершить работу; в противном случае перейти к шагу 3. Шаг 3. Увеличить F на единицу и перейти к шагу 4. Шаг 4. Если F  [ 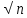] то сообщить: “n простое”, и завершить работу; в противном случае перейти к шагу 2.Мы описали способ определить, является ли число n>2 простым, и подсчитать его делитель, если n составное. Разумеется, если n простое, то мы находим и его разложение. Однако, если n составное, то нам хотелось бы найти все его делители и указать их кратности. Для этого достаточно применить описанный алгоритм несколько раз. Предположим, что в результате применения предыдущего алгоритма к n мы нашли делитель q1 этого числа. Тогда q1-его наименьший простой множитель. Применим тот же алгоритм к числу n/q1. Предположим, что число n/q1 составное и q2 — его наименьший простой делитель. Ясно, что q2 q1 Заметим, однако, что эти делители могут оказаться равными. Такая возможность реализуется, если n делится на 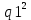 Продолжая в том же духе, мы применяем алгоритм к n/(q1q2) и т.д. В результате мы получаем последовательность простых чисел каждое из которых является делителем числа n Этой последовательности отвечает последовательность частных  Заметим, что это строго убывающая последовательность натуральных чисел, каждое из которых соответствует применению алгоритма деления методом проб к n. Поскольку множество натуральных чисел, меньших n конечно, после нескольких шагов мы получим полное разложение n на простые множители. Несложно проверить, что последнее число в последовательности частных равно 1, что и служит критерием завершения работы. Предположим теперь, что мы хотим представить разложение в том виде, в котором оно записано в теореме о разложении. Все простые делители нам известны, осталось лишь подсчитать их кратности. Для этого нужно вычислить, сколько раз каждый простой сомножитель встречается в указанной последовательности простых чисел. Разумеется, подсчет проще всего вести одновременно с их вычислением. Посмотрим на примере, как работает такой алгоритм. Допустим, мы хотим разложить число n=450 Алгоритм деления методом проб дает первый наименьший простой множитель 2. Повторное применение алгоритма, на этот раз к частному 450/2=225, дает множитель 3. Значит, делитель 3 числа 225 является и делителем числа 450. Применим алгоритм к числу 75=225/3. Вновь наименьшим делителем оказывается 3. Значит, 450 делится на  .Еще два выполнения алгоритма деления методом проб показывают, что 25 делится на 52, причем частное равно 1. Поэтому мы нашли полное разложение: 450= 2* * 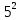.2. Специальный раздел2.1 Анализ требований к программному обеспечениюСуть использования данного подхода для шифрования лежит в задаче дискретного логарифмирования. Как и задача разложения на множители, она применяется во многих алгоритмах криптографии с открытым ключом. Предложенная в 1976 году У. Диффи и М. Хеллманом для установления сеансового ключа, эта задача послужила основой для создания протоколов шифрования и цифровой подписи и других криптографических протоколов. Асимметричный алгоритм Эль-Гамаля универсален. Он может быть использован для решения всех трех основных задач: для шифрования данных, для формирования цифровой подписи и для согласования общего ключа. Кроме того, возможны модификации алгоритма для схем проверки пароля, доказательства идентичности сообщения и другие варианты. Безопасность этого алгоритма, так же как и алгоритма Диффи-Хеллмана, основана на трудности вычисления дискретных логарифмов. Этот алгоритм фактически использует схему Диффи-Хеллмана, чтобы сформировать общий секретный ключ для абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ. Криптостойкость схемы Эль-Гамаля базируется на проблеме дискретного логарифма. Криптостойкость_способность криптографического_алгоритма противостоять криптоанализу.Стойким считается алгоритм, успешная атака на который требует от атакующего обладания недостижимым на практике объёмом вычислительных ресурсов или перехваченных открытых и зашифрованных сообщений либо настолько значительных затрат времени на раскрытие, что к его моменту защищённая информация утратит свою актуальность. В большинстве случаев криптостойкость не может быть математически доказана; можно только доказать уязвимости криптографического алгоритма либо (в случае криптосистем с открытым ключом) свести задачу взлома алгоритма к некоторой задаче, которая считается вычислительно сложной (то есть доказать, что взлом не легче решения этой задачи).Современная криптография в значительной мере использует результаты таких дисциплин как алгебра, теория чисел, теория сложности, поэтому необходимо знать математические основы криптографии. Среди этих основ одно из ведущих мест занимает проблема дискретного логарифмирования. Дискретное логарифмирование – задача обращения функции gx в некоторой конечной мультипликативной группе G. Для заданных g и a решение x уравнения  называется дискретным логарифмом элемента a по основанию g.Решение задачи дискретного логарифмирования состоит в нахождении некоторого целого неотрицательного числа x удовлетворяющего данному уравнению. Если оно разрешимо, у него должно быть хотя бы одно натуральное решение, не превышающее порядок группы. В отличие от логарифма непрерывного, дискретный логарифм не является дифференцируемой монотонной функцией, его нельзя найти приближенно, разложив в ряд Тейлора, и вообще никакого приближенного значения здесь не может быть, ведь x – целое число. Именно трудность решения этой задачи лежит в основе многих криптосистем. Это и шифр Эль-Гамаля, Шамира, такие крипто стандарты как подпись DSA , ГОСТ Р 34.10-94, ГОСТ Р 34.10-2001 и другие. Например, в шифре Эль-Гамаля, открытым ключом является тройка (p, g, y), закрытым ключом — число x, и связаны они между собой cоотношением y=  mod p. А процедура восстановления закрытого ключа по открытому есть решение задачи дискретного логарифмирования.Генерация ключей Генерируется случайное простое число p. Выбирается целое число g — первообразный корень p. Выбирается случайное целое число  такое, что 1Вычисляется  .Открытым ключом является тройка (p,q,y), закрытым ключом — число x. Зашифрование Отправитель выбирает случайное число k < p-1. Для которого НОД (k, p-1) =1; Вычисляет число a=gkmodp. Вычисляет число b=ykMmodp, где М – открытый текст. Шифртекстом является пара (a, b), шифр-текст в 2 раза длиннее открытого текста. Расшифрование: Зная закрытый ключ x, исходное сообщение можно вычислить из шифр текста ab по формуле:  При этом нетрудно проверить, что  и поэтому  . Для практических вычислении больше подходит формула: 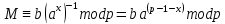 Пример: Шифрование Допустим, что нужно зашифровать сообщение {\displaystyle M=5}  .Произведем генерацию ключей: Пусть {\displaystyle p=11,g=2}p = 11,g = 2. Выберем {\displaystyle x=8}x = 8 - случайное целое число {\displaystyle x}x такое,что {\displaystyle 1 Вычислим {\displaystyle y=g^{x}{\bmod {p}}=2^{8}{\bmod {11}}=3}y =  .Итак, открытым ключом является тройка {\displaystyle (p,g,y)=(11,2,3)}(p,g,y)=(11,2,3), а закрытым ключом - число {\displaystyle x=8}x = (8). Выбираем случайное целое число {\displaystyle k}k такое, что 1 Вычисляем число {\displaystyle a=g^{k}{\bmod {p}}=2^{9}{\bmod {11}}=512{\bmod {11}}=6}  .Вычисляем число {\displaystyle b=y^{k}M{\bmod {p}}=3^{9}5{\bmod {11}}=19683\cdot 5{\bmod {11}}=9}b=ykMmodp=  .Полученная пара {\displaystyle (a,b)=(6,9)}(a,b) является шифр текстом. Расшифрование Необходимо получить сообщение {\displaystyle M=5}M = 5 по известному шифр тексту {\displaystyle (a,b)=(6,9)}(a,b) = (6,9) и закрытому ключу {\displaystyle x=8}x=8. Вычисляем M по формуле: {\displaystyle M=b(a^{x})^{-1}{\bmod {p}}=9(6^{8})^{-1}\mod {11}=5}  Получили исходное сообщение {\displaystyle M=5}M = 5. Пример Разложение на множители   Если учесть, что из четных простых делителей числа может быть только 2, то можно уменьшить количество циклов в реализации алгоритма, добавив дополнительную проверку  Алгоритм разложения на простые множители также можно реализовать с использованием рекурсии:  2.2.Инструкция пользователя Рисунок 1 – Стартовое окно. Программа была разработана в виде консольного приложения: Она содержит функции автоматической генерации и ручного ввода на выбор.  Рисунок 2 – Введенные данные. После выбранного способа, нужно ввести данные для обработки, чтобы в дальнейшем была проверена электронная подпись.  Рисунок 3 – Проверка. Так как значения совпали, ЭЦП считается верной. ЗаключениеВ настоящее время электронная цифровая используется для идентификации отправителя документа, ускорения документооборота, а также для подтверждения неизменности и достоверности подписанной информации. Идея метода факторизации Ферма лежит в основе одних из самых быстрых алгоритмов для факторизации больших полупростых чисел — методе квадратичного решета и общем методе решета числового поля. Основное отличие метода квадратичного решета от метода Ферма заключается в том,что вместо_поиска_квадрата_в_последовательности находятся_пары_та_их_чисел,_чьи квадраты равны по модулю (каждая из этих пар может являться разложением числа . Затем уже среди найденных пар чисел ищется та пара, которая и является разложением числа . Список литературыВасильева, И. Н. Криптографические методы защиты информации: учебник и практикум для академического бакалавриата / И. Н. Васильева. — Москва: Издательство Юрайт, 2019. — 349 с. Иванов М.А., Чугунков И.В. Криптографические методы защиты информации в компьютерных системах и сетях: Учебное пособие / Под ред. М.А. Иванова. М.: НИЯУ МИФИ, 2012. – 400 с.: ил. Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М.: МЦНМО, 2003. — 328 с. — ISBN 5-94057-103-4. Архивная копия от 27 января 2007 на Wayback Machine Ишмухаметов Ш. Т. Методы факторизации натуральных чисел: учебное пособие. — Казань: Казан. ун., 2011. — 190 с. Коблиц Н. Курс теории чисел и криптографии. — 2-е. — М.: Научное издательство ТВП, 2001. — 254 с. — ISBN 5-94057-103-4. Нестеренко А. Введение в современную криптографию.Теоретико-числовые алгоритмы. — 2011. — 190 с. Приложения
|