макроэкономика курсач (1) (1). Курсовая работа по дисциплине Макроэкономика Антонова Анна Сергеевна
 Скачать 252.38 Kb. Скачать 252.38 Kb.
|
|
Федеральное государственное образовательное бюджетное учреждение высшего образования «Финансовый университет при Правительстве Российской Федерации» Департамент экономической теории ИНВЕСТИЦИИ И ЭКОНОМИЧЕСКИЙ РОСТ В МОДЕЛИ Р.СОЛОУ Курсовая работа по дисциплине:
Москва 2021 ОГЛАВЛЕНИЕ ВВЕДЕНИЕ 3 ГЛАВА I. История появилась неоклассическая модель экономического роста Р.Солоу. 6 ГЛАВА II. Экономическое и математическое содержание модели. 7 2.1. Накопление капитала. 8 2.1.1. Производственная функция и функция потребления в модели Р. Солоу. 8 2.1.2. Устойчивый уровень капиталовооружённости 12 2.1.3. Выбор оптимальной нормы накопления 14 2.2. Рост населения 17 2.2.1. Устойчивый уровень капиталовооружённости при росте населения 17 2.2.2. Последствия роста населения 19 2.3. Технологический прогресс 20 2.3.1. Устойчивый уровень капиталовооружённости при технологическом прогрессе 20 2.3.2. Последствия технологического прогресса 22 ГЛАВА III. Практическое применение модели Р. Солоу. 26 ЗАКЛЮЧЕНИЕ 29 СПИСОК ЛИТЕРАТУРЫ 30 ВВЕДЕНИЕ Проблема экономического роста во всём мире выдвигается в ряд первоочередных проблем экономического развития. В настоящее время дальнейшее развитие страны зависит от механизма экономического роста, позволяющего наиболее эффективно использовать достижения научно – технического прогресса. Мировая экономическая наука достаточно давно начала изучение тенденций экономического роста. Особую актуальность эта тема имеет для сегодняшнего этапа экономических реформ. Любые меры по реформированию экономики должны вписаться в общее тенденции экономического роста индустриально развитых стран на рубеже ХХ – ХХI века. Экономический рост стал постоянным явлением, что несмотря на некоторые снижения объёмов выпуска и даже глубокий спад производства долгосрочный тренд развития в экономике большей части стран мира носит устойчиво восходящий характер. Современный экономический словарь дает такое определение экономического роста: «Экономический рост - увеличение масштабов совокупного производства и потребления в стране, характеризуемое, прежде всего, такими макроэкономическими показателями, как валовой национальный продукт, валовой внутренний продукт, национальный доход. В общем виде экономический рост означает количественное и качественное изменение результатов производства и его факторов. Экономический рост - одна из главнейших целей для всех стран, в том числе и для России, где в данный период времени эта проблема особо актуальна. Поэтому содействие увеличению темпов экономического роста является одной из основных задач экономической политики государства, чему способствуют различные модели экономического роста, в том числе и модель Р. Солоу. Экономический рост сопровождается целым рядом количественных и качественных изменений в обществе, среди которых главенствующее положение занимает структурная трансформация экономики. Как и любые модели, модели роста представляют собой абстрактное, упрощённое выражение реального экономического процесса в форме уравнений или графиков. Задачами модели Р. Солоу являются ответы на следующие вопросы: каковы факторы сбалансированного экономического роста, как достичь экономического равновесия, какой темп роста может позволить себе экономика при заданных параметрах экономической системы, и как при этом максимизируются доходы населения и объем потребления. Модель даёт основу, с помощью которой можно проанализировать один из важнейших вопросов экономики: какая часть произведённого продукта должна потребляться сегодня, а какая его часть должна сберегаться для использования в будущем. Оценка разных вариантов политики требует взвешивания всех издержек и выгод выбора того или иного уровня сбережений. Данное исследование поможет объяснить причины изменения национального дохода во времени, а также межстрановые различия в этом показателе. Факторы производства (капитал и труд), а также производственная технология рассматриваются в качестве источников производства и, следовательно, дохода. Поэтому различия в доходе должны определяться различиями в капитале, труде и технологии. Теоретико-методологической основой и информационной базой исследования являются труды отечественных и зарубежных исследователей, посвященные вопросам экономической модели Роберта Солоу. Структура и объём работы. Курсовая работа состоит из введения, трёх глав и заключения (общий объём 35с., 7 рисунков, 1 таблицы), списка использованной литературы. Во введении обоснована актуальность курсовой работы, указаны цели и задачи. В первой главе «История появилась неоклассическая модель экономического роста Р.Солоу» кратко изучена история появления модели. Во второй главе «Экономическое и математическое содержание модели» рассмотренны. В третьей главе «Практическое применение модели Р. Солоу» проведен анализ экономической политики. В заключении сформулированы основные выводы. Итак, в модели Р. Солоу источниками экономического роста являются накопление капитала, рост населения и технологический прогресс. Исследуем влияние каждого источника на обеспечение более высокого уровня жизни, увеличение масштабов совокупного производства и потребления в стране, то есть на экономический рост. ГЛАВА I. История появилась неоклассическая модель экономического роста Р.Солоу. Модель экономического роста Солоу названа в честь американского экономиста Роберта Солоу и была разработана в 1950-1960 годах. Солоу впервые описал свою модель экономического роста в 1956 году в работе «Contribution to the Theory of Economic Growth», и до сих пор она остаётся главной теоретической базой для анализа связей между накоплением капитала, технологическим прогрессом, ростом населения и экономическим ростом. За свои работы Роберт Солоу был удостоен в 1987 году Нобелевской премии. Он автор многих фундаментальных работ по проблемам экономического роста, по теории капитала, прибыли и безработицы. Солоу признан в научных кругах не только своей страны, но и за рубежом, является почетным членом многих академий и университетов. Надо отметить, что в 1920-1950 годах реальные процессы экономического роста неплохо описывали кейнсианские модели Домара и Харрода. Кейнсианскими моделями экономического роста называют модели, в которых кейнсианские предпосылки и методы анализа экономической конъюнктуры в коротком периоде используются для описания экономических процессов в долгосрочном периоде3. Р. Харрод и Е. Домар независимо друг от друга построили простейшую модель экономического роста, соответствующую кейнсианской концепции функционирования национальной экономики. Также известна кейнсианская модель Калдора. Но для более поздних наблюдений наиболее успешно использовалась неоклассическая модель экономического роста Р. Солоу. Роберт Солоу показал, что нестабильность динамического равновесия в кейнсианских моделях была следствием невзаимозаменяемости факторов производства. Он использовал в своей модели функцию Кобба-Дугласа, в которой труд и капитал являются субститутами. ГЛАВА II. Экономическое и математическое содержание модели. Модель Роберта Солоу относится к неоклассическим моделям. Основными характеристиками неоклассических моделей экономического роста являются: предположение о функционировании экономики в условиях совершенной конкуренции, обеспечивающей гибкую систему цен и равенство цен факторов производства их предельной производительности; отсутствие функции совокупного спроса, поскольку гибкая система цен постоянно приравнивает объём совокупного спроса к объёму совокупного предложения; отсутствие функции инвестиций, так как при равновесии на рынке благ I=S (инвестиции равны сбережениям); представление технологии в виде производственной функции с взаимозаменяемыми факторами производства и постоянным эффектом масштаба. Р. Солоу показал, что нестабильность динамического равновесия в кейнсианских моделях была следствием невзаимозаменяемости факторов производства. Он использовал в своей модели функцию Кобба-Дугласа, в которой труд и капитал являются субститутами. Другими предпосылками анализа модели Солоу являются: убывающая предельная производительность капитала, постоянная отдача от масштаба, постоянная норма выбытия, отсутствие инвестиционных лагов. Взаимозаменяемость факторов (изменение капиталовооружённости) объясняется не только технологическими условиями, но и неоклассической предпосылкой о совершенной конкуренции на рынках факторов производства. При анализе модели будем использовать такую технику, чтобы иметь возможность описать изменения экономики во времени, сделать анализ динамическим, а не статическим. Модель экономического роста Роберта Солоу показывает, как сбережения, рост населения и технологический прогресс (источники роста) воздействуют на рост объёма производства во времени. 2.1. Накопление капитала. 2.1.1. Производственная функция и функция потребления в модели Р. Солоу. Производственная функция выпуска – показывает взаимосвязь между объемом используемых ресурсов и максимально возможным объемом выпуска готовой продукции. В зависимости от типа используемой технологии производства производственная функция особым образом характеризует взаимосвязь между факторами производства (Таким образом получаем основные виды производной функции – Линейная, Леонтьевская, Кобба-Дугласа, Комбинированная). Как правило для упрощения рассматривается двухфакторная производственная функция в качестве производственных факторов для которой выступают труд и капитал. y=Y/AL - производительность эффективного труда (т.е. какое количество единиц готовой продукции приходится на одного эффективного работника) k=K/AL - капиталловооруженность (т.е. какое количество капитала приходится на одного эффективного работника) k=sf(k)- (n+g+δ)k - уравнение роста Солоу. i=sf(k) - фактические инвестиции на единицу эффективного труда. i^R=(n+g+δ)k - необходимые инвестиции для поддержания капиталловооруженности на прежнем уровне. В случае, когда В стационарном состоянии k(t)=0 - капиталловооруженность не изменяется, таким образом уравнение роста Солоу примет следующий вид: s*f(k)-k(n+g+δ)=0 Далее, если будет известен конкретный вид производственной функции, подставив его в полученное выражение сможем найти значение капиталловооруженности в стационарном состоянии. Для того чтобы выписать уравнения динамики капитала и выпуска в системе, используя определение капиталловооруженности: k(t)=K(t)/A(t)L(t) и производительности труда получаем, что K(t)=k(t)*A(t)*L(t) и Y(t)=f(k(t))*A(t)*L(t) т.к. капиталловооруженность остается неизменной, то K(t)=A(t)L(t) и Y(t)=f(k*)A(t)L(t). Подставив в полученные выражения значения капиталловооруженности в стационарном состоянии и уравнений динамики знаний и численности найдем уравнения, описывающие динамику капитала и выпуска.                         i* y* i* k1 k* k2 n+g+δ i=sf(k) y=f(k) i^R=(n+g+δ)k 0 K=K/L y=Y/L График 1. Стационарное состояние. Анализ шоков. Шоком называется неожиданное изменение какого-либо экзогенного параметра модели ( При изменении какого-либо параметра модель оказывается не в стационарном состоянии, и таким образом начинается её движение к новому стационарному состоянию, перейдя в которое она продолжит развиваться в стационарном состоянии. Анализировать новое стационарное состояние проще всего с помощью следующего график: На графике 2 стационарная точка определяется точкой пересечения графиков i=sf(k) и i^R=(n+g+δ)k. При изменении одного из параметров (                       y* i* i^R=(n+g+δ)k i* k* k2 n+g+δ i=sf(k) y=f(k) i^R=(n+g+δ)k 0 K=K/L y=Y/L График 2. Анализ стационарного состояния. На графике 2 мы видим, что изменилась g в результате чего новая точка стационарного состояния должна быть в точке Золотое правило накопления. Состояние экономики называется «золотым правилом накопления», при котором реальное потребление максимально из всех возможных. Объем реального потребления можно регулировать, изменяя норму сбережений. Норма сбережения должна быть такой, чтобы объем продукции, идущей на продажу, был максимален, но при этом объем инвестиций оставался достаточным для дальнейшего производства. Таким образом необходимо максимизировать величину Если удельное потребление будет максимально, и, следовательно, и реальное потребление также будет максимально. c(t)=C(t)/A(t)L(t) - удельное потребление (потребление на единицу эффективного труда) Учитывая, что C(t)=(1-s)Y(t) получаем: c(t)= C(t)/A(t)L(t)=(1-s)Y(t)/A(t)L(t)=(1-s)y(t)=y(t)-sy(t)=f(k(t))-sf(k(t)) Далее, используя условие стационарного состояния sf(k(t))=(n+g+δ)k(t), получаем: c(k(t))=f(k(t))-(n+g+δ)k(t) Так как мы находимся в стационарном состоянии, т.е. k(t-1)=k(t)=k*, то индекс t можно опустить. Итак c(k*)=f(k*)-( n+g+δ)k* - из этого уравнения, после подстановки конкретного вида производственной функции можно найти такое значение капиталловооруженности при котором удельное потребление будет максимально. Условие максимума данной функции: dc(k*)/dk*=0 Решив данное уравнение, мы найдем значение капиталловооруженности при котором удельное потребление будет максимально. Из уравнения стационарного состояния значение нормы сбережения, при которой удельное потребление будет максимально и, следовательно, сможем найти динамику реального потребления (Подставив в уравнение c(t)=(1-s)Y(t) значение нормы сбережения и динамики выпуска). 2.1.2. Устойчивый уровень капиталовооружённости Представив две главные составляющие модели Солоу - производственную функцию и функцию потребления - можно проанализировать, как накопление капитала обеспечивает экономический рост. Запасы капитала могут изменяться по двум причинам: 1. Инвестиции приводят к росту запасов капитала. 2. Часть капитала амортизируется, что приводит к уменьшению его запасов. Так как i = sy, то i = sf (k) Чем выше уровень капиталовооружённости k, тем выше объём производства и больше инвестиции. Чтобы учесть в модели амортизацию, предположим, что ежегодно выбывает определённая доля капитала д. д - норма выбытия. Таким образом, количество капитала, выбывающего за год, составляет дk. Выразим влияние инвестиций и выбытия на запасы капитала: Дk = i - дk, где Дk - изменение запасов капитала на одного работника. Иначе можно записать: Дk = sf(k) - дk. На рисунке 1 показано, что существует единственный уровень капиталовооружённости, при котором инвестиции равны величине износа. Если в экономике достигнут именно такой уровень, то он не будет изменяться во времени. При данном уровне капиталовооружённости Дk = 0. Эта ситуация называется состоянием устойчивой капиталовооружённости k*.                     Инвестиции и выбытие i2 Капиталовооружённость Дk1 i1 i*=Дk* k1 k* k2 k sf(k) Дk  ДK2 Рисунок 1. Инвестиции, выбытие и устойчивый уровень капиталовооружённости. При k Устойчивый уровень капиталовооружённости соответствует равновесию экономики в долгосрочном периоде. Независимо от первоначального объёма капитала, с которым экономика начинает развиваться, она затем достигает устойчивого состояния. Рассмотрим, что происходит в экономике, когда возрастает норма сбережений. На рисунке 3 представлены последствия такого изменения. 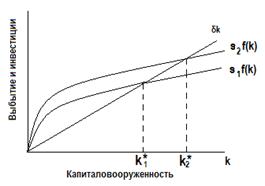 Рисунок 3. Рост нормы сбережений. Предположим, что экономика начинает развиваться, находясь в устойчивом состоянии при норме сбережений s1 и запасах капитала k1*. Норма сбережений затем возрастает до s2, вызывая соответствующий сдвиг вверх кривой sf(k). Сразу после повышения нормы сбережений инвестиции увеличиваются, но запас капитала и, следовательно, выбытие остаются пока неизменными. В итоге инвестиции компенсируют выбытие капитала. Капитал будет постепенно расти до тех пор, пока экономика не достигнет нового устойчивого состояния k2* с большей капиталовооружённостью и более высокой производительностью труда. Модель Солоу показывает, что норма сбережений является ключевой детерминантой величины устойчивой капиталовооружённости. Если норма сбережения более высока, то экономика будет иметь больший запас капитала и более высокий уровень производства. Увеличение нормы сбережений обеспечивает рост до тех пор, пока экономика не достигнет нового устойчивого состояния. Если в экономике поддерживается высокая норма сбережений, то и капиталовооружённость, и производительность будут высоки, но сохранить высокие темпы экономического роста навечно не удастся. 2.1.3. Выбор оптимальной нормы накопления Оптимальная норма накопления, соответствующая «золотому правилу» Э. Фелпса, обеспечивает равновесный экономический рост с максимальным уровнем потребления. Устойчивый уровень фондовооруженности, соответствующий этой норме накопления, обозначим к**, а потребления — с**. Уровень потребления в расчете на одного занятого при любом устойчивом значении фондовооруженности к* определяется путем ряда преобразований исходного тождества: y=c+i Выражаем потребление с через у и i и подставляем значения данных параметров, которые они принимают в устойчивом состоянии: c=y-i, c*=f(R*)-nd R* где с* — потребление в состоянии устойчивого роста; i = MPS х х f(k) = nd к по определению устойчивого уровня фондовооруженности. Теперь из различных устойчивых уровней фондовооруженности (к*), соответствующих разным значениям MPS, необходимо выбрать такой, при котором потребление достигает максимума (рис. 17.7). 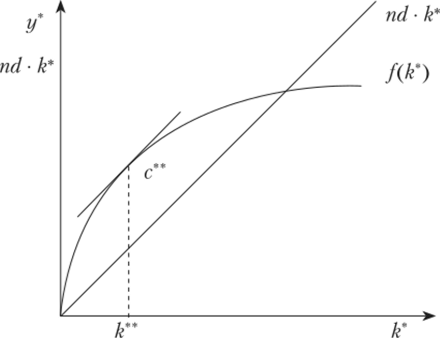 Рисунок 4. Устойчивый уровень потребления Если выбрано k* < к**, то объем выпуска увеличивается в большей степени, чем величина выбытия (линия / (k*) на графике круче, чем nd • &*), а значит, разница между ними, равная потреблению, растет. При k* > k** увеличение объема выпуска меньше роста выбытия, т.е. потребление падает. Рост потребления возможен лишь до точки k**, где оно достигает максимума (производственная функция и кривая nd • k* имеют здесь одинаковый наклон). В этой точке увеличение запаса капитала на единицу даст прирост выпуска, равный предельному продукту капитала (МРК), и увеличит выбытие на величину nd (износ на единицу капитала). Роста потребления не будет, если весь прирост выпуска будет использован на увеличение инвестиций для покрытия выбытия. Таким образом, при уровне фондовооруженности, соответствующем «золотому правилу» (&**), должно выполняться условие МРК = nd (предельный продукт капитала равен норме выбытия), а с учетом роста населения и технологического прогресса МРК = nd + / + g. Если экономика в исходном состоянии имеет запас капитала больший, чем следует по «золотому правилу», необходима программа по снижению нормы накопления. Эта программа обусловливает увеличение потребления и снижение инвестиций. При этом экономика выходит из состояния равновесия и вновь достигает его при пропорциях, соответствующих «золотому правилу». Если экономика в исходном состоянии имеет запас капитала меньший, чем k* необходима программа, направленная на повышение нормы сбережения. Эта программа первоначально приводит к росту инвестиций и падению потребления, но по мере накопления капитала с определенного момента потребление вновь начинает расти. В результате экономика достигает нового равновесия, но уже в соответствии с «золотым правилом», где потребление превышает исходный уровень. Данная программа обычно считается непопулярной в связи с наличием переходного периода, характеризующегося падением потребления, поэтому ее принятие зависит от межвременных предпочтений политиков, их ориентации на краткосрочный или долгосрочный результат. 2.2. Рост населения 2.2.1. Устойчивый уровень капиталовооружённости при росте населения Влияние роста население на устойчивое состояние - влияние роста населения (наряду с инвестициями и выбытием капитала) на капиталовооруженность труда. Инвестиции увеличивают запас капитала, а выбытие его уменьшает. Рост численности работников ведет к сокращению капиталовооруженности каждого из них. Так, к = K/L - есть капитал на 1 работника и у = Y/L - это выпуск продукции на 1 работника. С течением времени количество работников будет расти. Изменение запаса капитала, приходящегося на одного работника, составит: ∆к = i - σк - nк.Правая часть этого уравнения показывает влияние инвестиций, выбытия капитала и роста населения на величину капиталовооруженности. Инвестиции увеличивают k, a выбытие капитала и рост населения уменьшают ее. Частный случай, когда n=0. Для того, чтобы воспользоваться этим равенством, заменим i на sf(k) и перепишем его: ∆к = sf(k) - (σ + n)к. Эффекты выбытия капитала и роста населения теперь объединены. Уравнение показывает, что рост населения уменьшает капиталовооруженность таким же образом, как и выбытие. Рост населения уменьшает к, распределяя капитал между большим количеством работающих. Составляющую (σ+ n)k можно рассматривать как критическую величину инвестиций*. Это инвестиции, необходимые для поддержания запаса капитала, приходящегося на одного работника, на постоянном уровне. Критический уровень инвестиций обеспечивает возмещение выбытия капитала, которое равно σк. Он также включает инвестиции, необходимые для обеспечения капиталом в прежнем объеме новых работников. Необходимые для этих целей инвестиции составляют nk, поскольку на каждого работника приходится n новых работников и так как есть необходимый уровень капиталовооруженности. 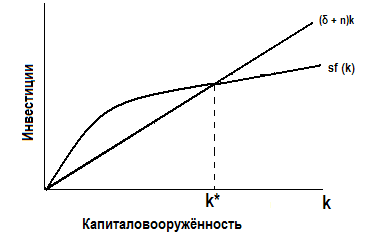 Рисунок 5. Учёт роста населения в модели Солоу. Экономика находится в устойчивом состоянии, если капитал на одного работника к неизменен. Устойчивый уровень капиталовооруженности - к*. Если к меньше, чем к*, то фактические инвестиции больше их критической величины, и к растет. Если к больше, чем к*, инвестиции меньше, чем критические, и к падает В устойчивом состоянии положительное влияние инвестиций на величину капиталовооруженности в точности компенсирует негативное влияние выбытия капитала и роста населения. Так, в точке к ∆к=0 и i = σк + nк. Если экономика достигла состояния устойчивости, инвестиции имеют две цели и две составляющие. Одна из них - замена изнашиваемого капитала,а другая - обеспечение новых рабочих капиталом на уровне устойчивого состояния (составляющая nk"). 2.2.2. Последствия роста населения Устойчивый равновесный рост в модели Солоу имеет место тогда, когда реальный объем национального производства увеличивается темпом, равным темпом прироста населения и занятости. При этом выполняется условие: предельный продукт капитала равен норме выбытия капитала (обновления или норме амортизации). Рост населения дополняет исходную модель Солоу по трём направлениям. Во-первых, он позволяет приблизиться к выяснению причин экономического роста, так как он объясняет непрерывный рост валового выпуска продукции. Во-вторых, рост населения влияет на уровень накопления капитала по Золотому правилу. Потребление на одного работника равно с = y – i. Поскольку устойчивый объём производства – это f(k*), а инвестиции устойчивого состояния – это (δ + n)k*, то устойчивый уровень потребления можно определить как c* = f(k*) – (δ + n)k* В-третьих, рост населения позволяет дать дополнительное объяснение того, почему некоторые страны богаты, а другие – бедны. На рисунке 6 показано, что увеличение темпа прироста населения с n1 до n2 уменьшает капиталовооружённость устойчивого состояния с k1* до k2*. Если k* уменьшается, а y* = f(k*), то производительность y* тоже снижается. 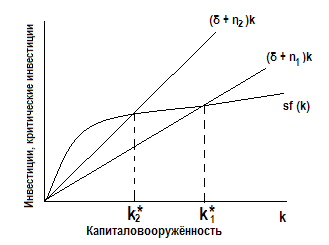 Рисунок 6. Влияние роста населения. Так модель Солоу предсказывает, что страны с более высоким темпом роста населения будут иметь меньшую капиталовооружённость и, следовательно, более низкий уровень ВНП на душу населения. 2.3. Технологический прогресс 2.3.1. Устойчивый уровень капиталовооружённости при технологическом прогрессе Теперь включим в модель Солоу технологический прогресс - третий источник экономического роста. Для этого вспомним производственную функцию, которая записывалась так: Y = F (K, L) Запишем производственную функцию следующим образом: Y = F(K, LЧE), где E - эффективность труда одного работника. Она зависит от здоровья, образования и квалификации рабочей силы Составляющая LЧE представляет собой рабочую силу, измеренную в единицах труда с неизменной эффективностью. В соответствии с новой производственной функцией общий объём производства Y зависит от количества единиц капитала K и от числа эффективных единиц рабочей силы, то есть от LЧE. Простейшим допущением технологического прогресса является то, что он вызывает прирост эффективности труда E с постоянным темпом g. Например, если g = 0,02, то отдача от каждой единицы труда увеличивается на 2 % в год: объём производства возрастает так, как если бы рабочая сила за год выросла на 2 %. Эта форма технологического прогресса называется трудосберегающей, а g называется темпом трудосберегающего технологического прогресса Замков, О.О. Математические методы в экономике / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных. - М: Издательство «Дело и сервис», 1997. Поскольку рабочая сила L растёт с темпом n, а отдача от каждой единицы труда E растёт с темпом g, то общее количество эффективных единиц труда LЧE растёт с темпом n+g. Пусть k = K/(LЧE) есть капитал на единицу труда с постоянной эффективностью, a y = Y/(LЧE) - объём производства на единицу труда с постоянной эффективностью. Поэтому можно записать: y = f(k). Анализ экономики происходит по той же схеме, что и в случае с ростом населения. Уравнение, показывающее изменение k с течением времени, теперь выглядит следующим образом: Дk = sf(k) - (д + n +g)k Если величина g велика, то общее количество единиц труда с постоянной эффективностью растёт быстро, а прирост капитала на такую единицу труда сравнительно мал и может стать отрицательным. На рисунке 7 показано, что имеется один уровень k*, при котором капитал и выпуск на единицу труда постоянны. Это устойчивое состояние представляет собой долгосрочное равновесие экономики. 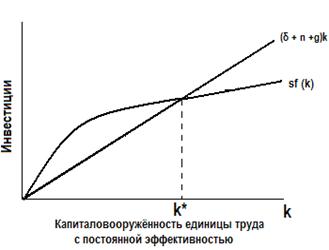 Рисунок 7. Технологический прогресс. При устойчивом состоянии экономики инвестиции sf(k) в точности компенсируют уменьшение k вследствие выбытия, роста населения и технологического прогресса. 2.3.2. Последствия технологического прогресса Рассмотренная модель Солоу позволяет описать механизм долгосрочного экономического роста, сохраняющий равновесие в экономике и полную занятость факторов. Она выделяет технический прогресс как единственную основу устойчивого роста благосостояния и позволяет найти оптимальный вариант роста, обеспечивающий максимум потребления. Представленная модель не свободна и от недостатков. Модель анализирует состояния устойчивого равновесия, достигаемые в длительной перспективе, тогда как для экономической политики важна и краткосрочная динамика производства и уровня жизни. Многие экзогенные переменные модели Солоу - s, d, n, g - было бы предпочтительнее определять внутри модели, поскольку они тесно связаны с другими ее параметрами и могут видоизменять конечный результат. Модель не включает также целый ряд ограничителей роста, существенных в современных условиях - ресурсных, экологических, социальных. Используемая в модели функция Кобба--Дугласа, описывая лишь определенный тип взаимодействия факторов производства, не всегда отражает реальную ситуацию в экономике. Эти и другие недостатки пытаются преодолеть современные теории экономического роста. В неоклассической модели роста объём выпуска в устойчивом состоянии растет с темпом (n+g), а выпуск на душу населения - с темпом g, т.е. устойчивый темп роста определяется экзогенно. Современные теории эндогенного роста пытаются определить устойчивый темп роста в рамках модели, эндогенно, связывая его со всеми возможными количественными и качественными факторами: ресурсными, институциональными и др. Сторонники концепции "экономики предложения" полагают, что увеличение темпов роста при полной занятости возможно прежде всего путём сокращения регулирующего вмешательства извне в рыночную систему. Характеристику изменения некоторых переменных модели Солоу с учётом технологического прогресса даёт таблица 1. Таблица 1. Устойчивый рост в модели Солоу с учётом технологического прогресса
Таким образом, с учётом технологического прогресса модель Солоу в конце концов может объяснить, почему уровень жизни растёт из года в год. Технологический прогресс по-разному влияет на экономический рост. Развивающиеся страны и страны с переходной экономикой, как правило, имеют на мировом рынке доступ к инвестиционным товарам, которые в промышленно развитых странах находятся на заключительных стадиях жизненного цикла. В основе сдвигов в отраслевой структуре национального хозяйства лежит цикличность рынков: их возникновение, развитие и упадок. “Жизненный цикл” отрасли определяется механизмами и динамикой перераспределения капиталов и рабочей силы. «Жизненные циклы» и смена поколений технологии воздействуют на отраслевую структуру по двум направлениям. Первое направление — новая технология, воплощенная в новой продукции, ранее не существовавшей на мировом рынке, становится основой для организации новой отрасли. В этом случае новое производство привлекает материальные, денежные, трудовые ресурсы, создаются новые мощности, оборудуются новые рабочие места. Новое производство “обрастает” производственно-техническими и сбытовыми связями, умножая спрос со стороны сопряженных отраслей самим своим появлением и ростом. Второе направление — частичная или полная смена технологической основы отрасли — ведется с целью улучшить качественные характеристики изделий, уже имеющихся на рынке. Главная задача — снизить издержки: добиться экономии сырья, энергии, замены живого труда работой машин. В этом случае техническое обновление отрасли обычно требует капиталовложений для замены оборудования и относительно уменьшает потребности в продукции сопряженных отраслей или в трудовых ресурсах вплоть до их вытеснения. В реальной экономике оба направления обычно сосуществуют одновременно. Модель Солоу показывает, что только технологический прогресс может объяснить непрерывно растущий уровень жизни. Введение в модель технологического прогресса изменяет также условия выполнения Золотого правила. Золотое правило для накопления капитала определяет устойчивый уровень, при котором максимизируется потребление на единицу труда с постоянной эффективностью. Теперь можно выразить этот уровень следующим образом: c* = f(k*) - (д + n + g)k* Устойчивый уровень потребления максимизируется, если: MPK = д + n + g, MPK - д = n + g Поскольку в реальных условиях экономика испытывает воздействие как роста населения, так и технологического прогресса, необходимо использовать это условие для выявления избытка или недостатка капитала по сравнению с устойчивым состоянием по Золотому правилу. Таким образом, в модели Солоу найдено объяснение механизма непрерывного экономического роста в режиме равновесия при полной занятости ресурсов. ГЛАВА III. Практическое применение модели Р. Солоу. Взаимосвязь различных источников экономического роста в модели Роберта Солоу раскрыта. Поэтому теперь можно приступить к анализу экономической политики по этому вопросу. Если национальная норма сбережений слишком низка, то государственная политика может привести к её увеличению двумя путями: непосредственно, через увеличение государственных сбережений и косвенно - через стимулирование увеличения частных сбережений. Говоря о практическом применении модели Р. Солоу, надо также отметить, что многие меры государственной политики ориентированы на стимулирование технологического прогресса путём поощрения научных исследований. Например, закон о налогах предоставляет льготы научно-исследовательским организациям, патентная система даёт временную монополию изобретателю нового продукта и так далее. С помощью модели Солоу можно решить вопрос об избытке или недостатке капитала в российской экономике. При этом следует рассматривать два периода: 1992-1998 годы и 1999-2003 годы (периоды спада и роста). В таблице приложения 1 представлены данные расчетов за 1992-2003 годы. Данные, требующие денежной оценки, выражены в трлн. рублей до 1998 года, а с 1998 года - в млрд. рублей в текущих ценах. Функция Кобба-Дугласа 1992-1998 годах выглядит так: Коэффициент 2.362 говорит о том, что рост заработной платы отставал от роста экономики, экономика стала больше эксплуатировать труд. Спад осуществлялся за счет остатка Р. Солоу (-2,07), то есть неидентифицируемых факторов. На долю прироста капитала приходилось 7,4% роста ВВП. С учетом чистого экспорта модель выглядит следующим образом: Далее определим количество капитала в экономике, для чего необходимо посчитать чистый предельный продукт капитала и сравнить его с темпами роста ВВП (приложение 2). Как видно, избыток капитала наблюдался только в 1997 году. Экономика находилась в состоянии намного ниже золотого правила модели Роберта Солоу. В таких случаях необходимо проводить экономическую политику, направленную на рост нормы сбережений и инвестиций. Рассмотрим теперь вклад в ВВП расходов на социально-культурные мероприятия. Из уравнения видно, что расходы на социально-культурные мероприятия положительно связаны с экономическим ростом. Поэтому они являются удобным объектом вложения государственных расходов в условиях, когда экономика испытывает недостаток капитала. Теперь повторим процедуры для периода 1999-2003 гг. Составим обычную модель Р. Солоу: Таким образом, в период данный период рост экономики был обусловлен неидентифицируемыми факторами (+3,304). Введем переменную изменения чистого экспорта. То, что чистый экспорт не объясняет изменений ВВП, объясняется тремя причинами роста после августа 1998 года. Во-первых, обычно принято связывать экономический рост с личностью Президента РФ. Во-вторых, с эффектом девальвации и конъюнктурой сырьевых рынков (внешние причины). В-третьих, рост носит восстановительный характер, экономика восстанавливается после трансформационного спада. В 1999-2003 годах доход на капитал отставал от роста ВВП. Это можно объяснить тем, что восстановление экономики шло на старых мощностях. То есть экономика росла вопреки состоянию основных фондов, что отражено в отрицательном значении коэффициента перед приростом капитала. Итак, модель Р. Солоу можно применить для объяснения экономических процессов, протекающих в России в разные периоды времени. ЗАКЛЮЧЕНИЕ В результате проведённого исследования были получены ответы на поставленные вопросы, а именно: какую роль играют в модели Р. Солоу источники экономического роста и каким образом, как достичь экономического равновесия, каковы причины изменения национального дохода во времени, как можно практически применять модель в экономическом анализе. Модель Роберта Солоу позволяет найти оптимальный вариант роста, обеспечивающий максимум потребления. Однако представленная модель имеет и свои недостатки. Хотя модель Р. Солоу представляет собой хорошую базу для анализа экономического роста, она является лишь первой его ступенью. Модель анализирует состояния устойчивого равновесия, достигаемые в длительном периоде, тогда как для экономической политики важна и краткосрочная динамика производства и уровня жизни. Также модель не включает целый ряд ограничителей роста, существенных в современных условиях - ресурсных, экологических, социальных. Используемая в модели функция Кобба-Дугласа не всегда отражает реальную ситуацию в экономике. Именно поэтому учёные, изучающие экономический рост, пытаются построить более сложные модели, которые позволять исследовать более широкий круг проблем. Модель Р. Солоу показывает, что продолжительный рост уровня жизни может иметь место только в результате технологического прогресса. Поэтому наше понимание экономического роста будет неполным, пока мы не поймём, как решения частных лиц и государственная политика воздействуют на технологический прогресс. Пока это - вопрос, требующий дальнейшего изучения. СПИСОК ЛИТЕРАТУРЫ (https://www.bestreferat.ru/referat-198637.html) (https://studwood.ru/783430/ekonomika/istoriya_poyavleniya_neoklassicheskoy_modeli_ekonomicheskogo_rosta_solou) (https://economicus.ru/site/grebenikov/E_Macro/chap14/14_2/14_2.html) (https://gigabaza.ru/doc/98644.html) (https://studbooks.net/1720039/ekonomika/nakoplenie_kapitala) (https://yandex.ru/search/?text=2.1.3) (https://infopedia.su/15x162b.html) (https://knigi.studio/makroekonomika/model-rsolou-posledstviya-uvelicheniya-tempa-103739.html) (https://www.stud24.ru/economic/model-jekonomicheskogo-rosta-r-solou/79387-248629-page2.html) (https://studbooks.net/1720041/ekonomika/tehnologicheskiy_progress) (https://studwood.ru/783434/ekonomika/posledstvie_tehnologicheskogo_progressa) (https://studbooks.net/1720042/ekonomika/prakticheskoe_primenenie_modeli_solou) |
