Курсовая работа по дисциплине Математическая логика и теория алгоритмов Анализ трудоемкости алгоритмов
 Скачать 138 Kb. Скачать 138 Kb.
|
|
Федеральное государственное автономное образовательное учреждение высшего профессионального образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» Институт Космических и Информационных Технологий институт Прикладной математики и компьютерной безопасности кафедра КУРСОВАЯ РАБОТА по дисциплине Математическая логика и теория алгоритмов Анализ трудоемкости алгоритмов Вариант № 3 Преподаватель: _________________ ________ Н. А. Богульская Должность, ученая степень дата, подпись инициалы, фамилия Студент: КИ 13-01 № 031312076 _________ Е.А. Борисюк номер группы номер зачетной книжки дата, подпись инициалы, фамилия Красноярск 2014 СОДЕРЖАНИЕ Введение………………………………………………………………….…..3 Постановка задачи…………….………………………………………….….4 Описание алгоритма…………………………………………...………….…5 Листинг программы…………………………………………...……………..7 Анализ трудоёмкости алгоритма…………………………………………...10 Список использованных источников...…………………………………….11 ВВЕДЕНИЕ Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды. Многие пытались решить эту задачу как теоретически, так и практически, во время прогулок. Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог. В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них. Ответ был «нельзя». Решение задачи по Эйлеру На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам: Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин. Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине. Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком. На рисунке 1 видно, что граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды. 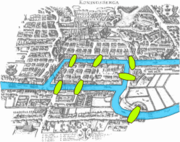   Рисунок 1 Созданная Эйлером теория графов нашла очень широкое применение в транспортных и коммуникационных системах (например, для изучения самих систем, составления оптимальных маршрутов доставки грузов или маршрутизации данных в Интернете). П  остановка задачи остановка задачи(Задача Эйлера). Задана схема мостов между островами и берегами реки в некотором городе. Спроектировать, если это возможно, экскурсионный маршрут, так чтобы он начинался и заканчивался в заданном пункте и проходил по каждому мосту ровно 1 раз. ОПИСАНИЕ АЛГОРИТМА Для решения задачи необходимо реализовать алгоритм нахождения эйлерового цикла. Алгоритм: Данные: Связный граф G = <V,E> без вершин нечетной степени, представленный списками ЗАПИСЬ[v],v ϵ V Результаты: Эйлеров цикл, представленный последовательностью вершин в стеке СЕ. 1. begin 2. СТЕК := Ø; СЕ := Ø; 3. v:=произвольная вершина графа; 4. CTEK <=v; 5. while СТЕК ≠ Ø do 6. begin v:= top(СТЕК);(*v=верхний элемент стека*) 7. if ЗАПИСЬ[v] ≠ Ø then 8. begin u:=первая вершина списка ЗАПИСЬ[v]; 9. СТЕК <=u; (*удалить ребро {v, u} из графа*) 10. ЗАПИСЬ[v] := ЗАПИСЬ[v]\{u}; ЗАПИСЬ[u] := ЗАПИСЬ[u]\{v}; 11. v := u 12. end 13. else (*ЗАПИСЬ[v] = Ø*) 14. begin v <=СТЕК, CE <=u 15. end 16. end 17. end Принципы действия алгоритма можно объяснить следующим образом: пусть v0 — вершина, выбранная в строке. Цикл 5 начинает строить путь с началом в v0, причем вершины этого пути помещаются в СТЕК, а ребра удаляются из графа. Эти действия продолжаются вплоть до того момента, когда путь нельзя удлинить, включив в него новую вершину, т.е. когда ЗАПИСЬ[v] = Ø в строке 7. Отметим, что тогда должно быть v = v0, так как в любом другом случае это означало бы, что степень вершины v нечетная. Таким образом, из нашего графа был удален цикл, а вершины этого цикла находятся в стеке СТЕК. Отметим, что в графе, модифицированном таким способом, степень произвольной вершины останется четной. Вершина v = v0 переносится теперь из стека СТЕК в стек СЕ, а «очередной» вершиной u становится верхний элемент стека СТЕК. Процесс повторяется, начиная с этой вершины (если ЗАПИСЬ[v] ≠ Ø ), в результате чего вследствие четности степени всех вершин находится и помещается в стек СТЕК, некоторый цикл, проходящий через вершину v. Это продолжается до того момента, когда СТЕК не станет пустым. Очевидно, что вершины, помещаемые в стек СЕ, образуют некоторый путь, причем вершина v переносится в стек СЕ только тогда, когда ЗАПИСЬ[v] = Ø, т.е. когда все ребра, инцидентные с этой вершиной, представлены (парами соседних вершин) в одном из стеков. Отсюда легко следует, что по окончании алгоритма стек СЕ содержит эйлеров цикл. Листинг программы #include "stdafx.h" #include #include #include "windows.h" #include using namespace std; struct Node { int inf; Node *next; }; //============================Stack============================== void push(Node *&st,int dat) { // Загрузка числа в стек Node *el = new Node; el->inf = dat; el->next = st; st=el; } int pop(Node *&st) { // Извлечение из стека int value = st->inf; Node *temp = st; st = st->next; delete temp; return value; } int peek(Node *st) { // Получение числа без его извлечения return st->inf; } //============================================================== Node **graph; // Массив списков смежности const int vertex = 1; // Первая вершина void add(Node*& list,int data) { //Добавление смежной вершины if(!list){list=new Node;list->inf=data;list->next=0;return;} Node *temp=list; while(temp->next)temp=temp->next; Node *elem=new Node; elem->inf=data; elem->next=NULL; temp->next=elem; } void del(Node* &l,int key) { // Удаление вершины key из списка if(l->inf==key){Node *tmp=l; l=l->next; delete tmp;} else { Node *tmp=l; while(tmp) { if(tmp->next) // есть следующая вершина if(tmp->next->inf==key) { // и она искомая Node *tmp2=tmp->next; tmp->next=tmp->next->next; delete tmp2; } tmp=tmp->next; } } } int eiler(Node **gr,int num) { // Определение эйлеровости графа int count; for(int i=0;i { //проходим все вершины count=0; Node *tmp=gr[i]; while(tmp) { // считаем степень count++; tmp=tmp->next; } if(count%2==1)return 0; // степень нечетная } return 1; // все степени четные } void eiler_path(Node **gr) { //Построение цикла Node *S = NULL;// Стек для пройденных вершин int v=vertex;// 1я вершина (произвольная) int u; push(S,v); //сохраняем ее в стек while(S) { //пока стек не пуст v = peek(S); // текущая вершина if(!gr[v]){ // если нет инцидентных ребер v=pop(S); cout< } else { u=gr[v]->inf; push(S,u); //проходим в следующую вершину del(gr[v],u); del(gr[u],v); //удаляем пройденное ребро } } } int main() { SetConsoleCP(1251); SetConsoleOutputCP(1251); system("CLS"); cout<<"Количество вершин: "; int n; cin>>n; // Количество вершин int zn;// Текущее значение graph=new Node*[n]; for(int i=0;i for(int i=0;i for(int j=0;j { printf("Смежна ли вершина %d вершине %d ",i+1,j+1); cin>>zn; if (zn) add(graph[i],j); } cout<<"\n\nРЕЗУЛЬТАТ "; if(eiler(graph,n))eiler_path(graph); else cout<<"Граф не является эйлеровым."; cout< cin.get(); cin.get(); return(0); } АНАЛИЗ ТРУДОЕМКОСТИ АЛГОРИТМА При нахождении вычислительной сложности алгоритма за N возьмем количество пунктов, т.е. вершин графа. Оценим сложность всех функций, входящих в программу. Функция push считывает две переменные, следовательно, имеет оценку сложности O(1). Функция peek считывает одну переменную, следовательно, имеет оценку сложности O(1). Функция add содержит 2 цикла. Первый цикл считывает одну переменную, следовательно, имеет оценку сложности O(1). Второй цикл проходит значение от 0 до n-1 и имеет оценку O(N). Функция имеет оценку сложности O(1)+O(N)= O(N). Функция del содержит 2 цикла. Первый цикл считывает одну переменную, следовательно, имеет оценку сложности O(1). Второй цикл содержит в себе тройной цикл. Внешний цикл считывает одну переменную, следовательно, имеет оценку сложности O(1). Внутренний цикл считывает одну переменную, следовательно, имеет оценку сложности O(1). Вложенный в него цикл проходит значение от 0 до n-1 и имеет оценку O(N). Оставшиеся 2 вложенных в него цикла считывают одну переменную, следовательно, имеет оценку сложности O(1). Функция имеет оценку сложности O(1)O(N)O(1) O(1)= O(N) Функция eiler содержит 3 цикла. Первый цикл содержит 3 вложенных цикла и имеет оценку сложности O(N2). Второй цикл считывает одну переменную, следовательно, имеет оценку сложности O(1). Третий цикл также считывает одну переменную, следовательно, имеет оценку сложности O(1). Функция имеет оценку сложности O(1)+ O(1)+ O(N2)=O(N2). Функция eiler_path содержит 1 цикл и функцию push. Цикл содержит 2 вложенных цикла и имеет оценку сложности O(N). Функция имеет оценку сложности O(N). Функция main содержит 4 цикла, кроме того, функция содержит все вышеперечисленные функции. Первый цикл принимает значения от 0 до n-1 и имеет сложность O(N). Второй цикл содержит в себе еще один цикл. Оба цикла принимают значения от 0 до n-1, следовательно, оценка сложности O(N2). Оставшиеся циклы считывают одну переменную, следовательно, имеют оценку сложности O(1). Таким образом, суммарная оценка сложности алгоритма равна O(N2). СПИСОК ЛИТЕРАТУРЫ Лекция 8 «Анализ трудоемкости алгоритмов» из курса «Математическая логика и теория алгоритмов» В. Липский «Комбинаторика для программистов», 1988 О.П. Кузнецов, Г.М. Адельсон-Вельский «Дискретная математика для инженера», 1980 О. Оре «Теория графов», 1980 |
