Математические методы и модели исследования операций. Курсовая работа по дисциплине Математика Тема Математические методы и модели исследования операций
 Скачать 1.39 Mb. Скачать 1.39 Mb.
|
|
Математическое моделирование производственного раскроя 1.1 Постановка задачи На заводе на станках 4 типов изготавливается 9 видов продукции. Ежемесячный фонд станко-часов станков 1 типа составляет 2121 часов, 2 типа – 2021 часов, 3 типа – 2771 часов, 4 типа – 4292 часов. Производительность станков (станко-часы/1 ед. продукции) и себестоимость 1 ед. продукции, и потребности в продукции предприятия заданы в таблице 1. Из предыдущего опыта известны доли бракованной продукции (в виду различных причин – объективных и субъективных), они приведены в таблице 10. Бракованная продукция не реализуются, но затраты на ее изготовление учитываются в общей себестоимости. Готовая продукция условно реализуется в конце месяца, если продукции произведено больше спроса, она может храниться в течение месяца. В этом случае себестоимость хранимой продукции увеличивается на 5 %. Необходимо составить такой план помесячной загрузки станков, при котором общая себестоимость всей продукции была бы минимальна. Если двухмесячного фонда часов не хватит на удовлетворение имеющегося спроса на предстоящие два месяца, определить: 1) сколько дополнительных месяцев потребуется; 2) какой вид продукции и в каком количестве будет произведен в третьем и последующих месяцах (критерий тот же)? Таблица 1 – Данные к задаче 1.5.
Таблица 2 – Доля брака на станках
Построение математической модели поставленной задачи Переменные Необходимо решить сколько часов, какого вида продукции, какой станок будет производить и в каком месяце. Пусть 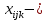 количество часов работы i станка над продукцией типа j в k месяце (где количество часов работы i станка над продукцией типа j в k месяце (где 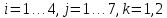 …). …).Ограничения Запишу условия целочисленности и неотрицательности переменных: 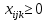 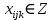 Известно, что ежемесячный фонд станко-часов 1 типа составляет 2521 часов, 2 типа – 2021 час, 3 типа – 2771 час, 4 типа 5292 часа. Это значит, что сумма часов работы каждого типа станка над всеми видами продукции не должна превышать соответствующий ежемесячный фонд станко-часов: 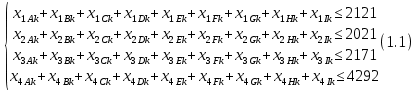 Приведём исходные данные и неизвестные величины к одной единице, в качестве которой возьмём 1 станко-час работы станка первого типа. Производительность станков 2, 3 и 4 типов равны соответственно 2, 2,5 и 3 от производительности станка первого типа (таблица 1). Следовательно, фактический фонд станко-часов станков 2, 3 и 4 типов будут равны соответственно 2, 2,5 и 3 от их изначального ежемесячного фонда станко-часов. Система 1.1 примет вид: 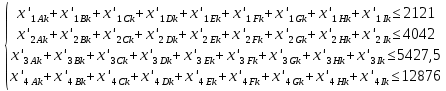 (1.2) (1.2)Над выпуском продукции А вида работают станки четырёх типов, сумма часов их работы над выпуском этой продукции должна быть не меньше, чем значение спроса на данную продукцию в этом месяце. Для составления неравенства выразим спрос на продукцию А вида в приведённых станко-часах, для этого умножим спрос на данную продукцию на производительность первого станка при производстве А вида товара: 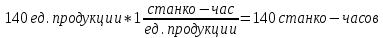 Аналогичные вычисления проведём для каждого вида продукции в первом и во втором месяце, составим неравенство, описывающее удовлетворение спроса на товар: Для первого месяца 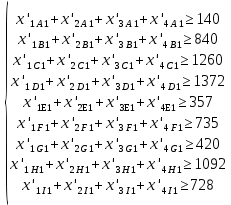 (1.3) (1.3)В условии сказано, что в конце месяца реализуется лишь качественная продукция (не бракованная). Если вероятность производства бракованной продукции А типа на станке 1 вида равна 0,025 (таблица 2), то вероятность производства качественной продукции А типа на станке 1 вида равна: 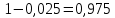 Проведу аналогичные вычисления для каждого типа продукции, произведённой на каждом виде станков. Полученные результаты занесу в таблицу 3. Таблица 3 – Доля производства качественной продукции
С учётом вероятности производства бракованной продукции система 1.3 примет вид: 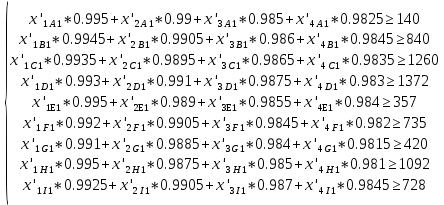 (1.4) (1.4)В условии сказано, что продукция может быть произведена сверх спроса, в таком случае эта продукция не реализуется и хранится на складе. Чтобы найти количество часов, затраченных на производство продукции сверх спроса необходимо из фактического количества часов, затраченных на производства товара вычесть количество часов, необходимых для удовлетворения спроса на данный товар в этом месяце. Обозначим часы работы станков над продукцией сверх спроса через переменную 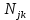 , вычислим её: , вычислим её: 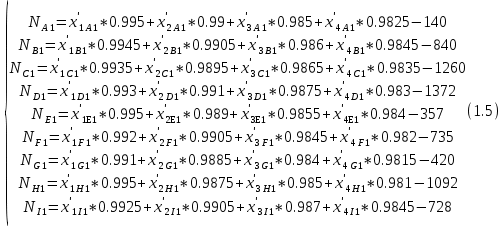 Так как излишки товаров с предыдущего месяца реализуются в последующем, то для второго месяца система 1.4 примет вид: 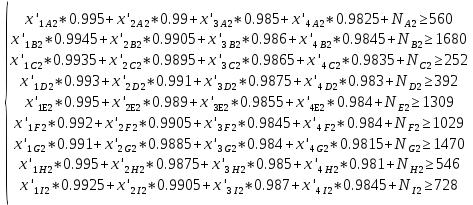 (1.6) (1.6)Часы работы станков над продукцией сверх спроса во втором месяце равны: 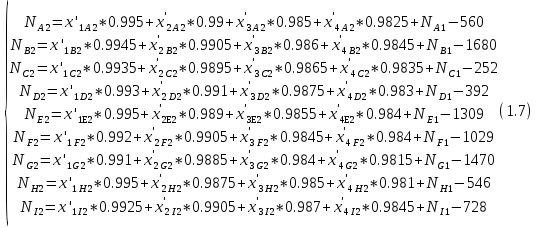 Где: 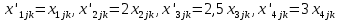 (1.8) (1.8)Целевая функция По условию задачи требуется минимизировать функцию себестоимости всей продукции. Себестоимость продукции равна количеству затраченных на её производство станко-часов, умноженных на стоимость одного часа. Так как производительность станков 2, 3 и 4 типов соответственно в 2, 2,5 и 3 больше, чем производительность станка первого типа, в приведённых станко-часах себестоимость продукции, произведённой на 2, 3 и 4 станках будет меньше соответственно в 2, 2,5 и 3 раза. Себестоимость часов работы станков в приведённых станко-часах вычислю и занесу в таблицу 4. Таблица 4 – Себестоимость продукции в приведённых станко-часах
В условии сказано, что себестоимость продукции, хранящейся на складе, увеличивается на 5%. Наценка на такую продукцию будет равна: 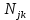 * себестоимость приведённого станко-часа * 0,05. * себестоимость приведённого станко-часа * 0,05.Таким образом, целевая функция будет складываться из: 1)Cуммы расходов на производство каждого вида продукции на всех станках в первом месяце; 2)Издержек на хранение излишек произведённой в первом месяце продукции; 3) Cуммы расходов на производство каждого вида продукции на всех станках во втором месяце; 4) Издержек на хранение излишек произведённой во втором месяце продукции. 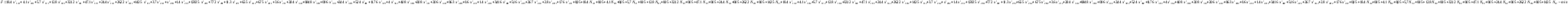 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
