МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ. Курсовая работа по дисциплине метрология, стандартизация и сертификация
 Скачать 2.56 Mb.
|
ЧАСТЬ 3ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ РАВНОТОЧНЫХ ИЗМЕРЕНИЙДисциплина — Метрология, стандартизация и сертификация Часть I — Обработка результатов многократных измерений Группа № 111111, номер по журналу — 176, студент — Дулов Шифр задания 111111 0 G 0.13 26.2 Результаты измерений 26.40 26.16 16.19 26.20 26.04 26.03 26.31 26.02 26.31 26.43 26.43 26.27 26.17 26.02 25.96 26.40 26.15 26.17 26.13 26.26 26.31 25.98 26.11 26.17 26.49 26.30 26.34 26.17 26.34 26.36 26.24 26.08 26.26 26.13 26.52 26.16 26.12 26.05 25.99 26.38 26.33 26.12 26.15 26.06 25.89 26.17 26.02 26.23 26.01 26.14 26.18 26.27 26.20 26.02 26.13 26.39 26.27 25.95 25.99 26.03 26.00 26.22 26.33 26.39 26.10 26.15 26.33 26.37 26.21 26.37 26.48 26.15 26.35 26.05 26.30 26.27 26.25 26.16 26.22 26.10 26.01 26.23 26.26 26.24 26.25 26.32 26.18 26.14 26.41 26.35 26.26 26.28 26.25 26.12 26.05 26.28 26.32 26.19 26.27 26.25 26.14 Определить вид ЗРВ по критерию Пирсона; Записать результат с доверительной вероятностью P = 0,96 Определение оценок числовых характеристик закона распределения вероятности результата измерений. Используя исходные данные, найдем значение среднего арифметического 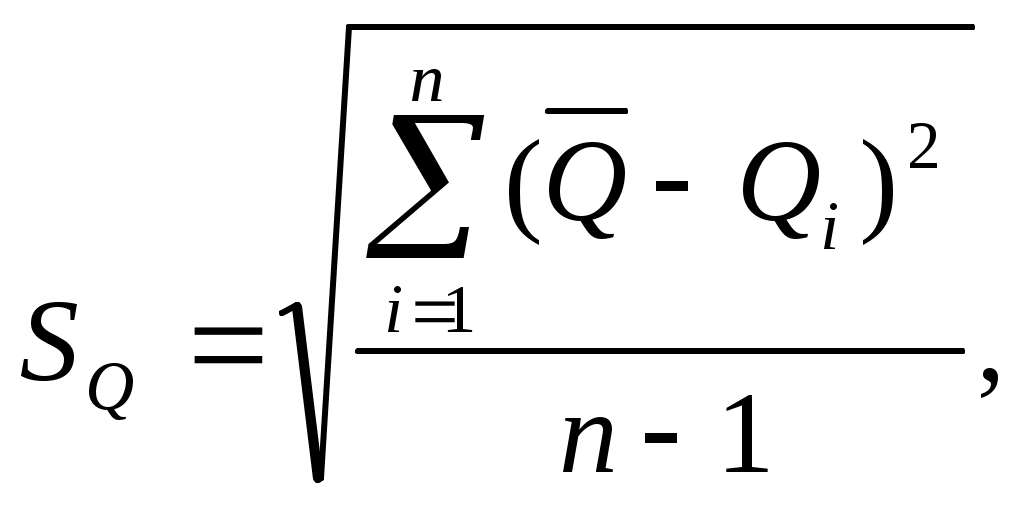 (1), которое является статической оценкой математического ожидания для ряда однородных результатов, и стандартное отклонение  (2), которое является статистической оценкой среднего квадратического отклонения:  (1)где  среднее арифметическое значение результатов измерений; количество измерений; номер измерений.   (2)где  стандартное отклонение результатов измерений; количество измерений; номер измерений. С помощью правила «трех сигм» проверим наличие грубых промахов. Вероятность того, что случайная величина отклонится от своего математического ожидания на большую величину, чем утроенное среднее квадратичное отклонение, практически равно нулю. Правило справедливо только для случайных величин, распределённых по нормальному закону.     Ни один из результатов не выходит за границы интервала  , следовательно, с вероятностью P=0,9973 гипотеза о наличии грубых промахов опровержена.Выявление вида закона распределения вероятности результата измерения Чтобы выдвинуть гипотезы о виде закона распределения вероятности строим гистограмму. Для построения гистограммы, необходимы результаты отдельных измерений расположить в вариационный ряд по возрастанию их численных значений. Так же следует определить  число результатов измерений, попавших в этот  интервал и  теоретическое число измерений, попавших в этот ряд.Таблица 7 Результаты отдельных измерений расположим в вариационный ряд по возрастанию их численных значений
Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разбивается на k=9 одинаковых интервалов  .Ширину интервала определим по формуле:  (3)Выбираем начало первого интервала так, чтобы его значение оказалось меньше минимального результата вариационного ряда, а последний интервал превышал бы максимальное значение ряда. Это позволит исключить совпадение каких-либо результатов с границами интервалов гистограммы. Для этой цели примем смещение s = 0,001. Начало первого интервала в точке, тогда конец последнего интервала окажется в точке. Начало первого интервала в точке  , тогда конец последнего интервала окажется в точке  .  Подсчитаем для каждого интервала количество результатов  , попавших в каждый отдельный интервал, используя формулу: (4)Учтем что, если в интервал попадает меньше пяти наблюдений, то такие интервалы необходимо объединить с соседними, соответственно изменяя и параметр . Так объединим в один первые два и последние два интервала. Общее число интервалов станет равным 7. Таблица 8
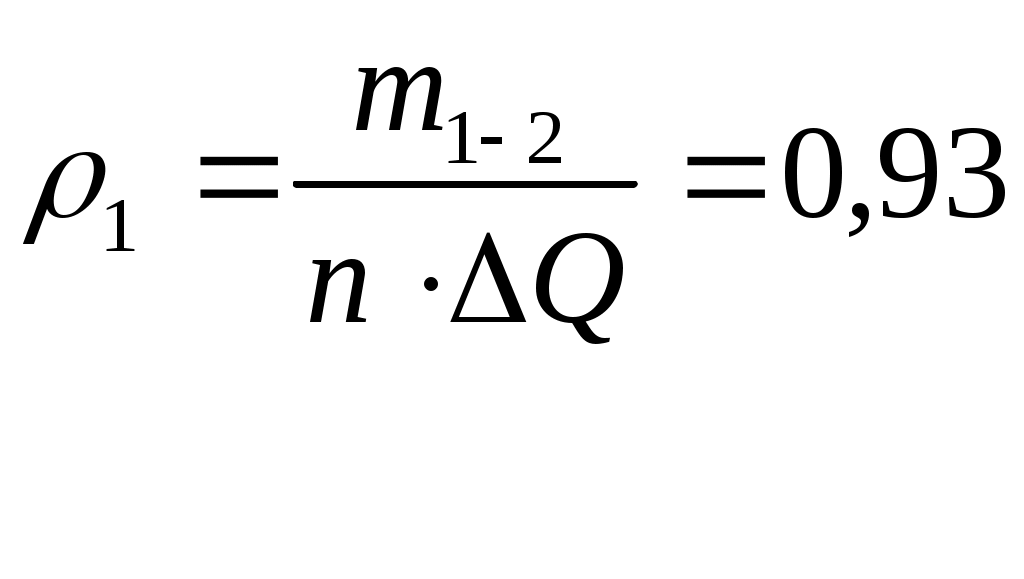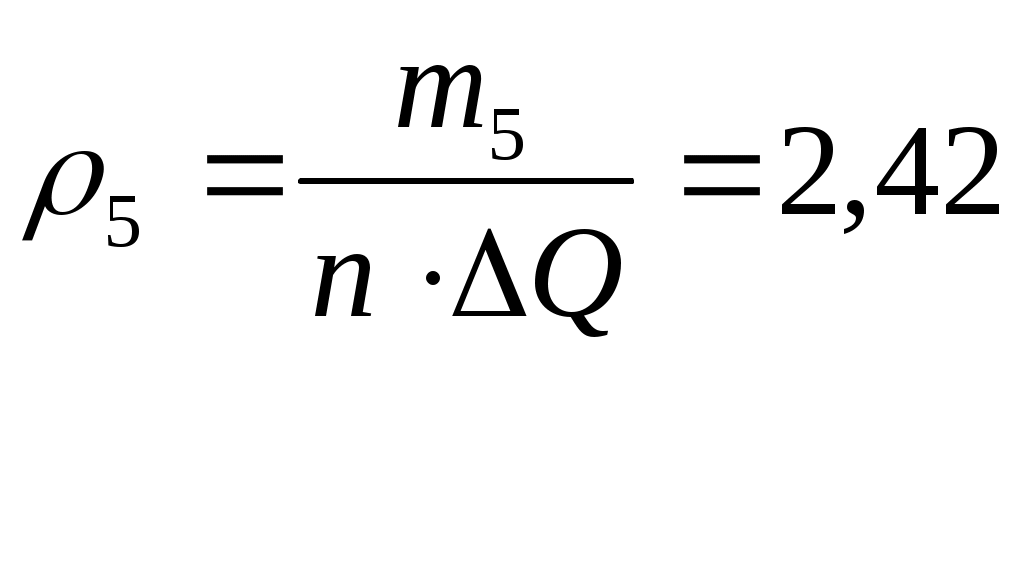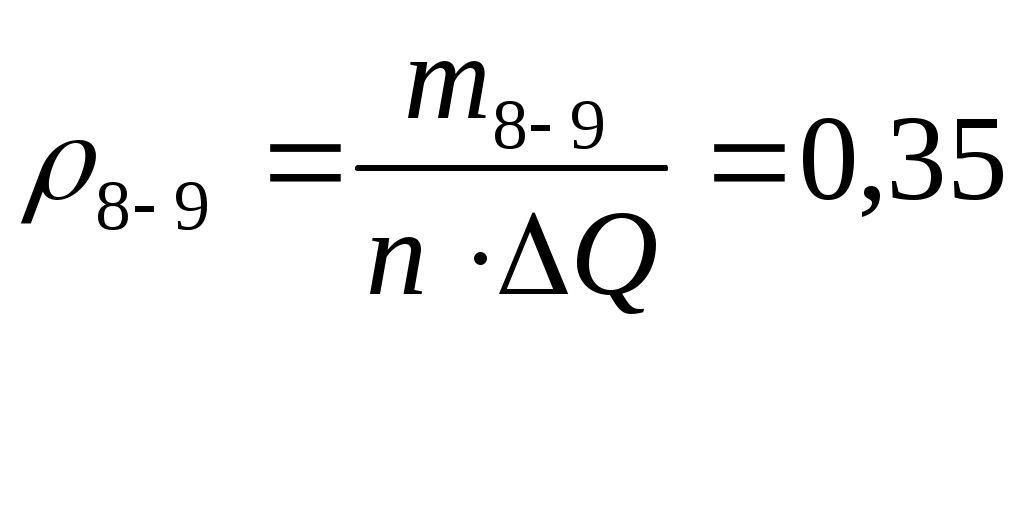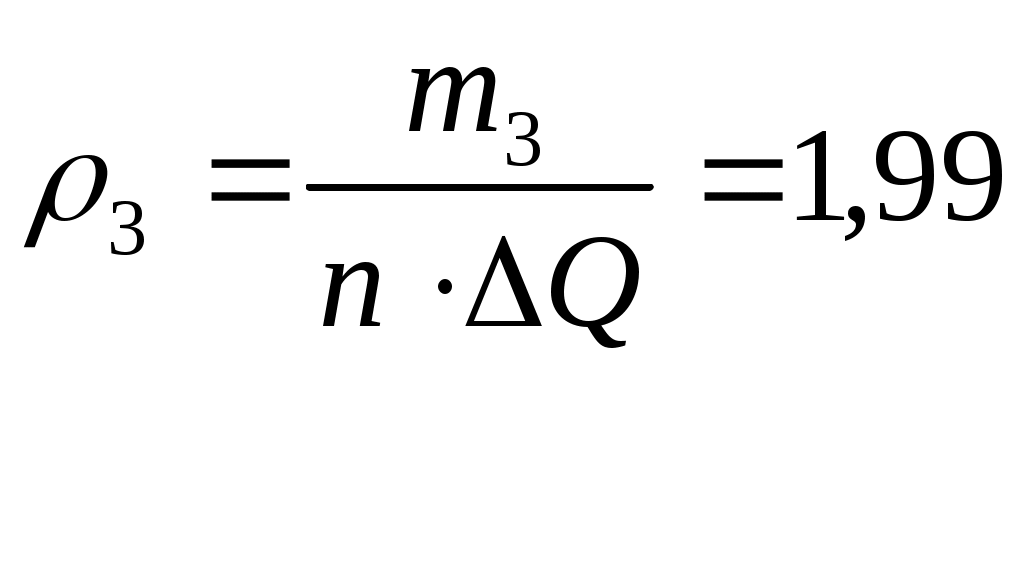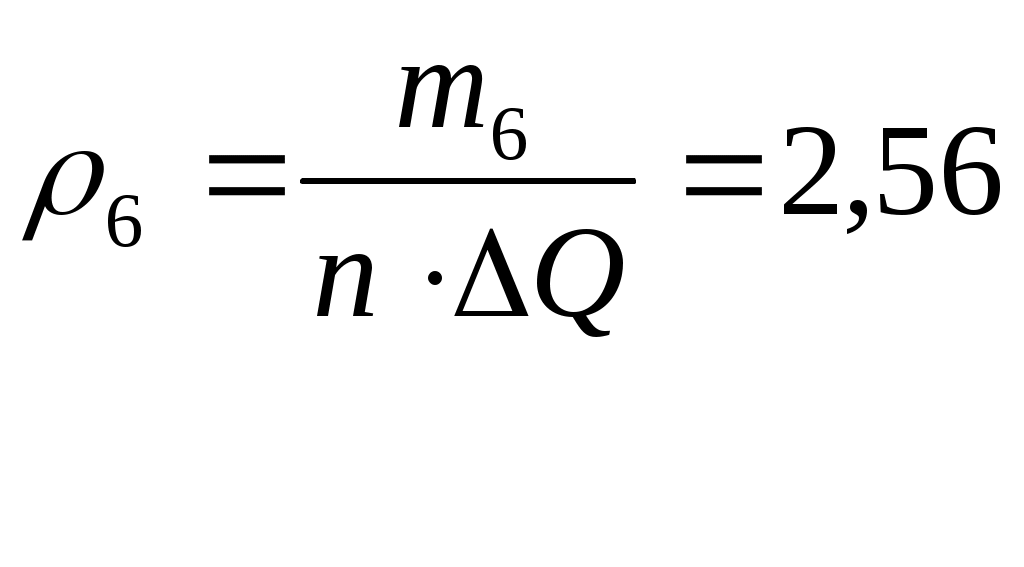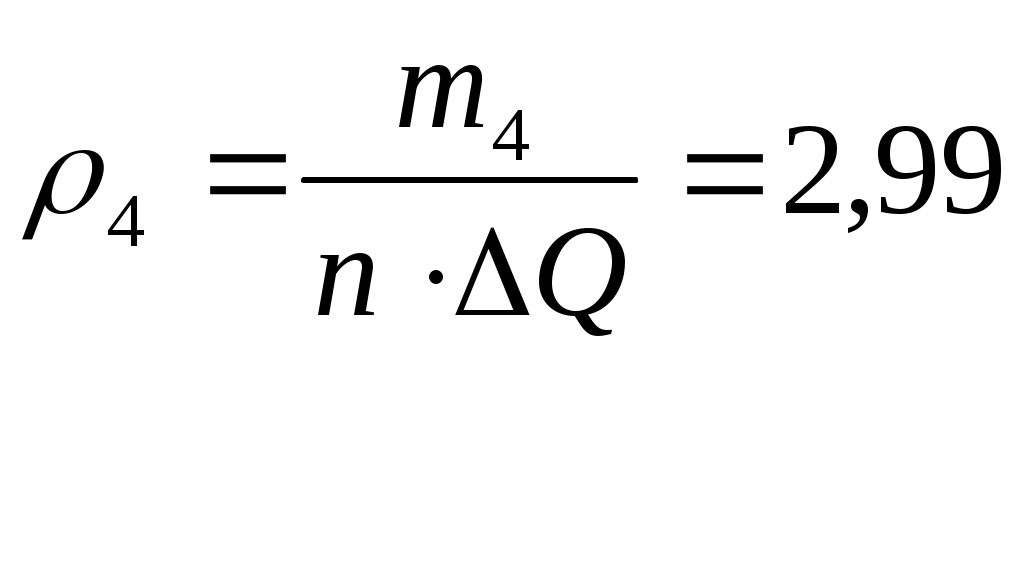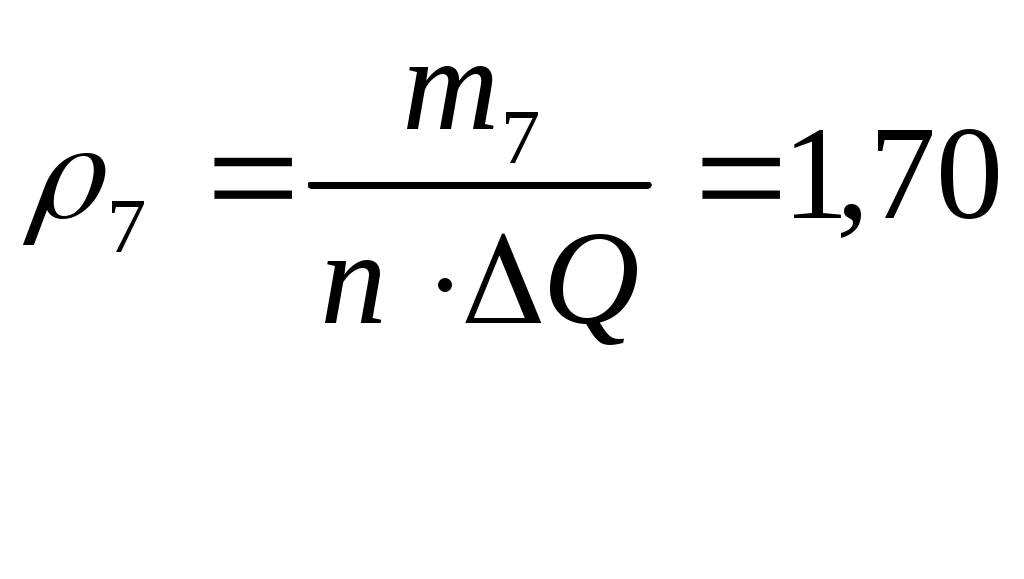       Результаты производимых вычислений занесем в таблицу 1 (см. прил. 1), а затем построим саму гистограмму (рис.1). Теоритическую кривую распределения плотности вероятности строим в тех же координатах, что и гистограмму. Рассчитанные данные возьмем из таблицы 9 столбец  (см. прил. 1).Строим саму гистограмму 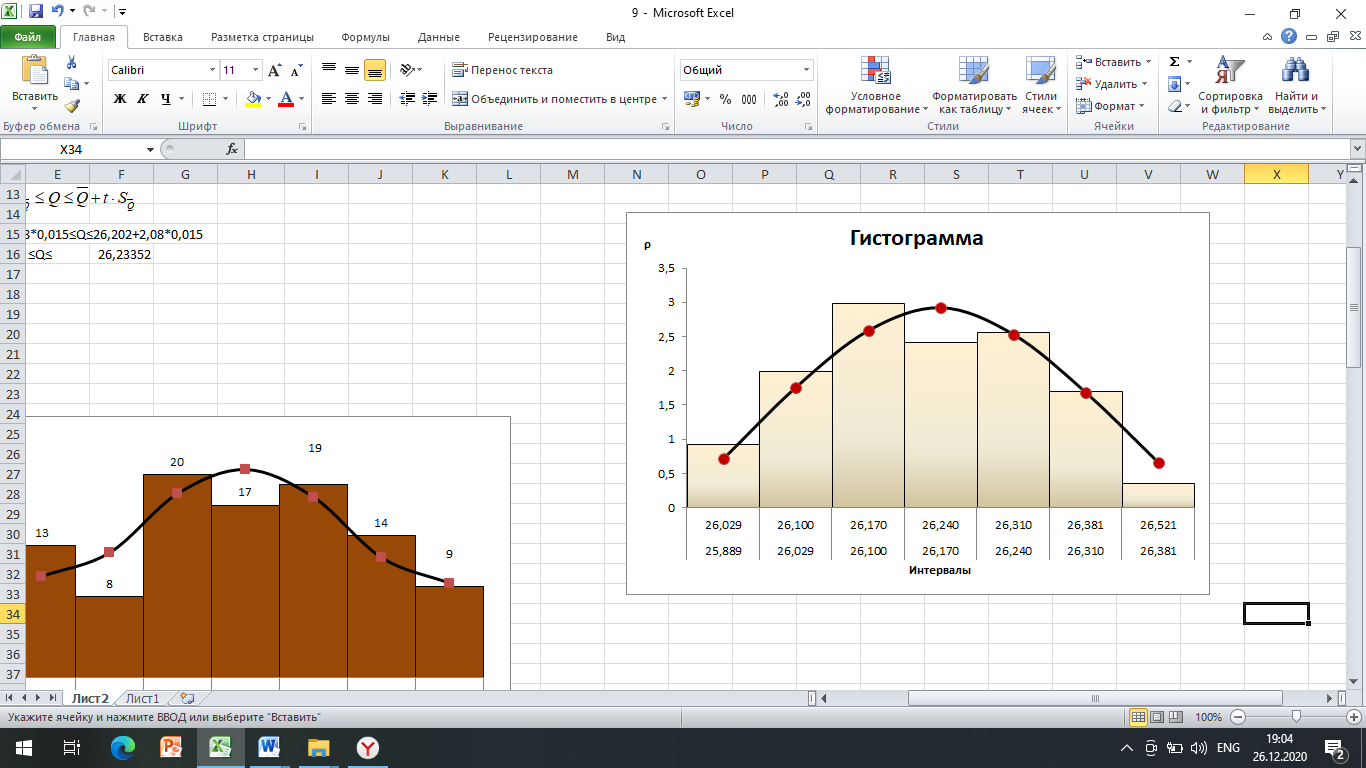 Рис.1 Гистограмма и выравнивающая нормальная кривая, иллюстрирующая гипотезу о виде ЗРВ Из вида гистограммы на рис.1 можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы. Проверка нормальности закона критерием Пирсона. Если выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используем функцию Лапласа:  ,где  – значения соответствующие началу и концу интервала.Для каждого из этих значений рассчитаем относительный доверительный интервал 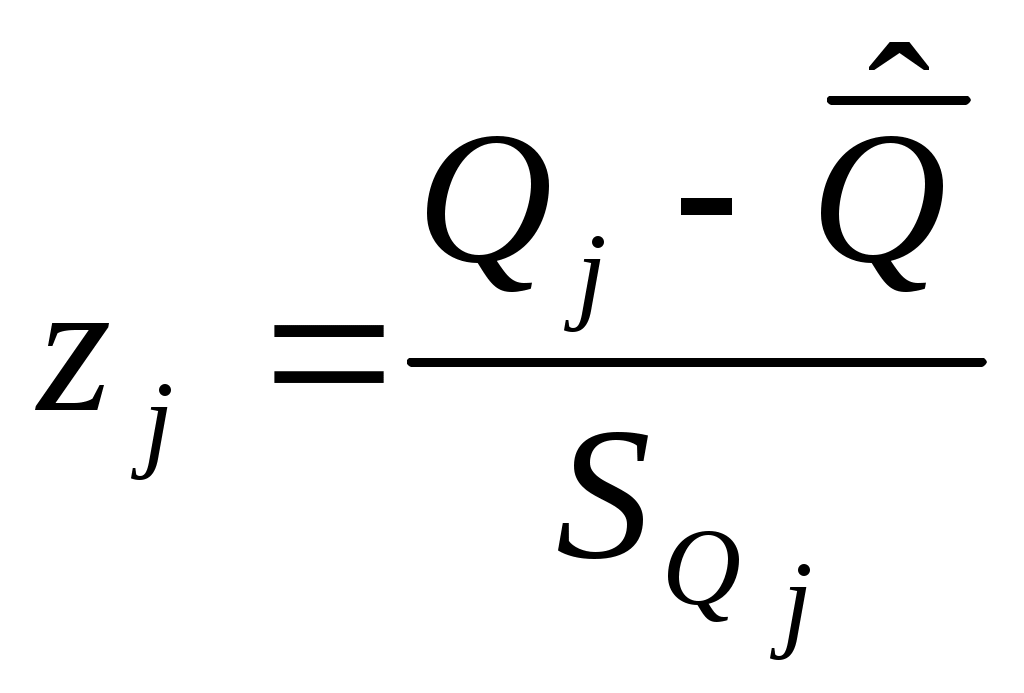 по формуле:  (5)Затем из таблиц Лапласа найдем соответствующие значения функций Ф(  ) и Ф( ). При этом будем иметь в виду, что конец предыдущего интервала является началом последующего .Произведем численный расчет. первый интервал:  ,  На основании вычисленных значений функции Лапласа получаем:  Значения критерия Пирсона для отдельного интервала рассчитываем по формуле:  , (6)где  – общее количество проведенных измерений,  – число результатов измерений, попавших в данный интервал.1) Поскольку конец предыдущего интервала является одновременно началом следующего, то теоретическая вероятность попадания результата определится по формуле. Началом первого интервала следует считать «–», а функции  2) По последнему столбцу рассчитаем значение  -критерия и определяем его суммарное значение: 3) Определим табличное (критическое) значение  -критерия Пирсона, задавшись доверительной вероятностью, равной 0,95 и вычислив число степеней свободы:  ,где k – число интервалов. Получаем:  Т.к.  , следовательно, с вероятностью 0,95 гипотеза о нормальности распределения вероятности результата измерения принимается.Представим результаты в виде доверительного интервала с доверительной вероятностью Р = 0,96. Для этого определим среднее квадратическое отклонение среднего арифметического |
