Курсовая работа по дисциплине Основы алгоритмизации и программирования
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МОСКОВСКИЙ ФИНАНСОВО-ПРОМЫШЛЕННЫЙ УНИВЕРСИТЕТ «СИНЕРГИЯ» КУРСОВАЯ РАБОТА
МОСКВА 2019 г. Оглавление Введение Понятие алгоритма Типы алгоритмов Свойства алгоритма Виды алгоритмов Базовые структуры алгоритмов Словестная форма записи алгоритмов и формульно-словестная Табличная форма записи алгоритма Программная форма записи алгоритма и псевдокод 2.4 Структура следования 2.5 Структура ветвления 2.6 Структура цикла Цикл с предусловием (цикл-пока) Цикл с полст-условием (до) 2.9 Понятие линейного алгоритма 2.10 Понятие разветляющегося алгоритма 2.11 Понятие цикличного алгоритма 3. Зачем нужны алгоритмы? Заключение Введение Вопрос актуальности выбранной мной курсовой работы по теме «Основные структуры алгоритмов: сравнительный анализ и примеры их использования» в принципе не появлялся у меня в голове, так как алгоритмы, их структуры, способы их применения-фундамент программирования. Эти знания необходимы для общего понимания работы алгоритмов, для понимания работы компьютеров. Предметом изучения являются алгоритмы, их структуры. Задачи курсовой работы состоят в том чтобы провести анализ алгоритмов и их структур и показать примеры их использования Понятие алгоритма Слово «Алгоритм» происходит от algorithmi – латинского написания имени аль-Хорезми, под которым в средневековой Европе знали величайшего математика из Хорезма (город в современном Узбекистане) Мухаммеда бен Мусу, жившего в 783-850 гг. В своей книге «Об индийском счете» он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных. Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, - процесс творческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. Другое дело – реализация уже имеющегося алгоритма. Ее можно поручить субъекту или объекту, который не обязан вникать в существо дела, а возможно, и не способен его понять. Такой субъект или объект принято называть формальным исполнителем. Примером формального исполнителя может служить стиральная машинаавтомат, которая неукоснительно исполняет предписанные ей действия, даже если вы забыли положить в нее порошок. Человек тоже может выступать в роли формального исполнителя, но в первую очередь формальными исполнителями являются различные автоматические устройства, и компьютер в том числе. Каждый алгоритм создается в расчете на вполне конкретного исполнителя. Те действия, которые может совершать исполнитель, называются его допустимыми действиями. Совокупность допустимых действий образует систему команд исполнителя. Алгоритм должен содержать только те действия, которые допустимы для данного исполнителя. [1, C4] Свойства алгоритма Данное выше определение алгоритма нельзя считать строгим - не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата». Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций. Такими свойствами являются: Дискретность (прерывность, раздельность) - алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего. Определенность - каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче. Результативность (конечность) - алгоритм должен приводить к решению задачи за конечное число шагов. Массовость - алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма. Правила выполнения арифметических операций или геометрических построений представляют собой алгоритмы. При этом остается без ответа вопрос, чем же отличается понятие алгоритма от таких понятий, как «метод», «способ», «правило». Можно даже встретить утверждение, что слова «алгоритм», «способ», «правило» выражают одно и то же (т.е. являются синонимами), хотя такое утверждение, очевидно, противоречит “свойствам алгоритма”. Само выражение «свойства алгоритма» не совсем корректно. Свойствами обладают объективно существующие реальности. Можно говорить, например, о свойствах какого-либо вещества. Алгоритм – искусственная конструкция, которую мы сооружаем для достижения определенных целей. Чтобы алгоритм выполнил свое предназначение, его необходимо строить по определенным правилам. Поэтому нужно говорить все же не о свойствах алгоритма, а о правилах построения алгоритма, или о требованиях, предъявляемых к алгоритму. Первое правило – при построении алгоритма, прежде всего, необходимо задать множество объектов, с которыми будет работать алгоритм. Формализованное (закодированное) представление этих объектов носит название данных. Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате своей работы выдает данные, которые называются выходными. Таким образом, алгоритм преобразует входные данные в выходные. Это правило позволяет сразу отделить алгоритмы от “методов” и “способов”. Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм. Второе правило – для работы алгоритма требуется память. В памяти размещаются входные данные, с которыми алгоритм начинает работать, промежуточные данные и выходные данные, которые являются результатом работы алгоритма. Память является дискретной, т.е. состоящей из отдельных ячеек. Поименованная ячейка памяти носит название переменной. В теории алгоритмов размеры памяти не ограничиваются, т. е. считается, что мы можем предоставить алгоритму любой необходимый для работы объем памяти. В школьной «теории алгоритмов» эти два правила не рассматриваются. В то же время практическая работа с алгоритмами (программирование) начинается именно с реализации этих правил. В языках программирования распределение памяти осуществляется декларативными операторами (операторами описания пе ременных). При запуске программы транслятор языка анализирует все идентификаторы в тексте программы и отводит память под соответствующие переменные. Третье правило – дискретность. Алгоритм строится из отдельных шагов (действий, операций, команд). Множество шагов, из которых составлен алгоритм, конечно. Четвертое правило – детерминированность. После каждого шага необходимо указывать, какой шаг выполняется следующим, либо давать команду остановки. Пятое правило – сходимость (результативность). Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма. Итак, алгоритм – неопределяемое понятие теории алгоритмов. Алгоритм каждому определенному набору входных данных ставит в соответствие некоторый набор выходных данных, т.е. вычисляет (реализует) функцию. При рассмотрении конкретных вопросов в теории алгоритмов всегда имеется в виду какая-то конкретная модель алгоритма. [1,c 6] Виды алгоритмов и их реализация Алгоритм применительно к вычислительной машине – точное предписание, т.е. набор операций и правил их чередования, при помощи которого, начиная с некоторых исходных данных, можно решить любую задачу фиксированного типа. Виды алгоритмов как логико-математических средств отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом: Механические алгоритмы, или иначе детерминированные, жесткие (например, алгоритм работы машины, двигателя и т.п.); Гибкие алгоритмы, например стохастические (вероятностные) и эвристические. 8 Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм. Вероятностный (стохастический) алгоритм дает программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата. Эвристический алгоритм (от греческого слова “эврика”) – это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так как не обозначена вся последовательность действий, не выявлены все действия исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения сходных задач. Линейный алгоритм – набор команд (указаний), выполняемых последовательно во времени друг за другом. Разветвляющийся алгоритм – алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов. Циклический алгоритм – алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы – последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторого условия. Вспомогательный (подчиненный) алгоритм (процедура) – алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний 9 (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм. [1,c 8] Базовые структуры алгоритмов В 1969 году Голландский учёный программист Эдсгер Вибе Дейкстра доказал: алгоритм для решения любой логической задачи можно составить только из структур: «Следование», «Ветвление», «Цикл». Такие структуры называются «Базовыми алгоритмическими струтурами» , структура программирования. Для описания структуры алгоритмов можно использовать 2 способа: Блок-схемы и Учебные алгоритмические языки программирования. Обозначения блок-схем  Рисунок 12 Источник 2 Рисунок 2 Источник 2  Учебные языки программирования  Рисунок 3 Источник 2 2.1 Словестная форма записи алгоритмов и формульно-словестная Перед изучением структуры алгоритмов надо понять, как же их представляют и записывают, первая форма записи алгоритмов Словестная. Такое описание алгоритма состоит из словесного перечня действий в виде предложений. Например, вычислить C= А-В, если А=В, A + B , если AB . Исходные данные А и В ввести в память ЭВМ, проверить выполнение неравенства АB. Если оно выполняется, то вычислить А-В. Результат обозначить как С и вывести его; в противном случае вычислить А+В, результат обозначить С и вывести его. Недостаток такого представления — отсутствие четкой формализации и наглядности выполнения процесса. Достоинством является то, что таким способом можно описывать алгоритмы с любою степенью детализации. Формульно-словесный способ основан на задании инструкций о выполнении конкретных действий в четкой последовательности в сочетании со словесными пояснениями. Для рассмотренного задания алгоритм, представленный формульно-словесным способом, будет следующим: Этап 1. Ввести А, В. Этап 2. Если АB, то перейти к этапу 4, иначе — к этапу 3. Этап 3. С=А-В, перейти к этапу 5. Этап 4. С=А+В. Этап 5. Принять значение С за результат. Этап 6. Вывести С. Этот способ более компактен, но не является строго формальным. [Ист.3] Табличная форма записи алгоритма Табличная форма записи алгоритма- это запись алгоритма в виде таблицы. Используемые таблицы могут быть различными. Порядок составление алгоритма: Переписать выражение так, как допустимо в информатике. Определить порядок действий. Ввести обозначения промежуточных результатов. Занести полученные действия в таблицу. Пример: Алгоритм вычисления R=2a +3b . [Ист.5]  Рисунок 4 Источник 4 Программная форма записи алгоритма и псевдокод Псевдокод. Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов. Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций. Программная форма записи алгоритма. При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм. Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы - компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем. Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке - программой для компьютера. Программа, создаваемая человеком - программистом, представляет собой текст, состоящий из знаков, как правило букв, цифр и специальных знаков. Знаки в тексте программы часто объединены в последовательности - ключевые слова, слова объединены в предложения языка программирования - операторы. Каждый оператор, как правило, записывается в отдельную строку текста программы. Таким образом текстовое программирование представляет собой иерархическую последовательность знаков, слов, операторов, записываемых и читаемых последовательно, как обычный текст человеческой письменности. Ниже показан пример записи текста программы на языке BASIC [Ист. 5]  Рисунок 5 Источник 5 Структура следования После изучения записи алгоритмов, можно начать изучение одной из основных тем курсовой работы: структуры алгоритмов. Первая из них самая простая и понятная-«Следование». Структура «Следования»-линейная последовательность действий 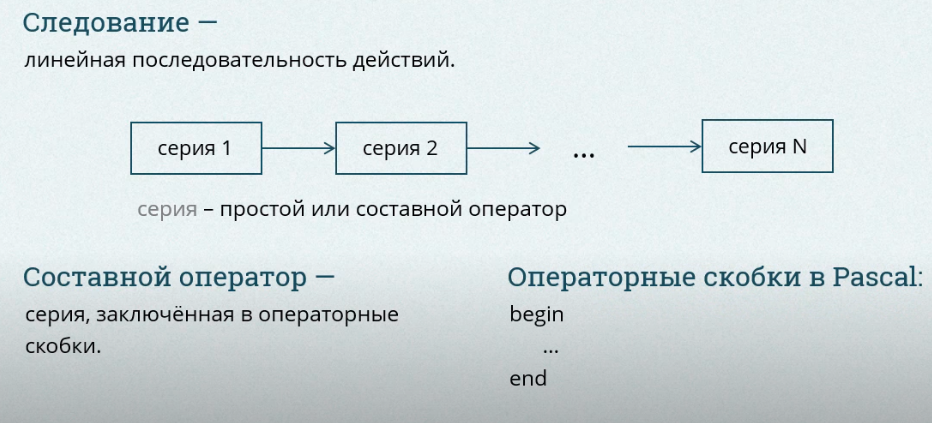 Рисунок 6 Источник 2 «Серия»-тут представляет составной оператор, в языке Pascal-это «begin», «end». 2.5 Структура ветвления Ветвление – это структура, обеспечивающая выбор между двумя альтернативами. Выполняется проверка, а затем выбирается один из путей. Эта структура называется также «ЕСЛИ – ТО – ИНАЧЕ», или «развилка». Каждый из путей (ТО или ИНАЧЕ) ведет к общей точке слияния, так что выполнение программы продолжается независимо от того, какой путь был выбран. Может оказаться, что для одного из результатов проверки ничего предпринимать не надо. В этом случае можно применять только один обрабатывающий блок (структура «ЕСЛИ – ТО»). Цикл «Пока» (цикл с предусловием) начинается с проверки логического выражения. Если оно истинно, то выполняется тело цикла, затем все повторяется снова, пока логическое выражение сохраняет значение «истина». Как только оно становится ложным, управление передается по программе дальше В цикле «До» (цикл с постусловием) проверка условия выполняется после операторов тела цикла. Цикл повторяется, если условие ложно. Как только оно становится истинным, управление передается по программе дальше . Пожалуй, самым важным достижением структурного подхода к разработке алгоритмов является нисходящее проектирование программ. Этот метод основан на идее уровней абстракции, которые становятся уровнями модулей в разрабатываемой программе. Это позволяет программисту сначала сконцентрировать внимание на определении того, что надо сделать в программе, а лишь затем решать, как это надо делать. При нисходящем проектировании исходная, подлежащая решению задача разбивается на ряд подзадач, подчиненных по своему содержанию главной задаче. Такое разбиение называется детализацией или декомпозицией. На следующем этапе эти задачи, в свою очередь, разбиваются на более мелкие подчиненные подзадачи и так далее, до уровня относительно небольших подзадач, которые требуют для решения небольших модулей. Модуль – это последовательность логически связанных операций, оформленных как отдельная часть программы. Модули связаны между собой только по входным и выходным данным. Использование модулей имеет следующие преимущества: 1) возможность создания программы несколькими программистами; 2) простота проектирования и последующих модификаций программы; 3) упрощение отладки программы – поиска и устранения в ней ошибок; 4) возможность использования готовых библиотек наиболее употребительных модулей. [Ист 1, стр 32] Структура цикла Алгоритм циклической структуры – это алгоритм, в котором предусмотрено неоднократное выполнение одной и той же последовательности действий. На практике часто встречаются задачи, в которых одно или несколько действий бывает необходимо повторить несколько раз. Многократное повторение последовательности действий называется циклом, а многократно повторяющиеся действия – телом цикла. Изучение циклов демонстрирует учащимся главное преимущество компьютера перед человеком – выполнение большого числа действий за короткое время. Ведь даже весьма короткий циклический алгоритм, составить который не так уж долго, при исполнении может потребовать выполнения нескольких сотен действий, с которыми компьютер справится намного быстрее, чем человек. Учащиеся должны уметь организовать цикл и верно определить тело цикла. Более того, при конструировании алгоритмов важно использовать такую конструкцию цикла, которая окажется оптимальной для решения поставленной задачи. Существует три формы циклов: цикл с параметром, цикл с предусловием, цикл с постусловием. Каждая форма имеет стандартное описание на языке схем, а также соответствующий оператор алгоритмического языка. 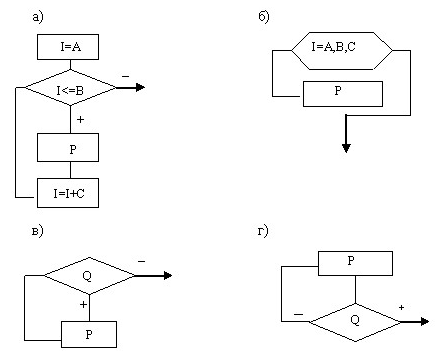 Рисунок 7 Источник 6 а), б) – циклическая структура “Для каждого” в) – циклическая структура “Пока” г) – циклическая структура “До” I – счетчик числа повторов, C – приращение счетчика, A – начальное значение счетчика, B – конечное значение счетчика, P – тело цикла. 1. Цикл “Для каждого” можно записать в следующем виде: Для каждого I от A до B с шагом С: P Конец цикла по I I – счетчик числа повторов, C – приращение счетчика, A – начальное значение счетчика, B – конечное значение счетчика, P – тело цикла. 2. Цикл “Пока” можно записать так: Пока Q повторять: P Конец цикла Q – условие. ЭВМ будет выполнять P до тех пор, пока условие Q истинно. 3. Цикл “До” записывается следующим образом: Повторять: P До выполнения Q Конец цикла Тело цикла P выполняется до тех пор, пока условие Q ложно. Одним из самых распространенных в практике вычислений алгоритмом циклической структуры является алгоритм вычислений некоторой функции y=f(x) для значений x, которые меняются от начального значения x0 до конечного xk с шагом h. Исходными данными алгоритма являются значения: x0, xk, h. Необходимо вычисления по формуле y=f(x) повторять (xk-x0)/h+1 раз, т. е. при построении алгоритма организовать цикл. Параметром цикла выберем переменную x. Схема алгоритма решения этой задачи на рис. 7. В схеме блок 3 присваивает начальное значение параметру цикла x, блок 6 осуществляет изменение на h параметра x при каждом выполнении цикла, блок 7 управляет циклом, для чего проверяется условие повторения цикла x<=xk. При выполнении этого условия (да) управление передается на начало цикла, а при невыполнении – осуществляется выход из цикла, т.е. переход к следующему по порядку блоку 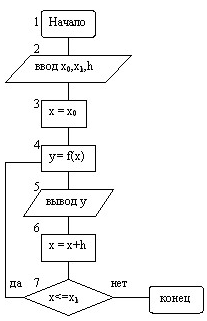 Рисунок 8 Источник 6 На собственном опыте я убедился, что учащиеся быстрее усваивают материал, выполняя практические работы, которые ценны своей наглядностью, за персональным компьютером. Поэтому рекомендую изучение циклических структур проводить на задачах с применением графических команд. [Ист 6] Цикл с предусловием (цикл-пока) После того как мы разобрали, что такое цикличная структура алгоритма, остались незакрытые вопросы по поводу того что такое «Цикличная структура пока» и «Цикличная структура пока», сейчас я расскажу о них. Циклы с предусловием используются тогда, когда выполнение цикла связано с некоторым логическим условием. Цикл с предусловием — цикл, который выполняется пока истинно некоторое условие, указанное перед его началом. Это условие проверяется до выполнения тела цикла, поэтому тело может быть не выполнено ни разу (если условие с самого начала ложно). Цикл называется итерационным, если число его повторений не задается, а определяется в ходе выполнения цикла. В этом случае одно повторение цикла называется итерацией. 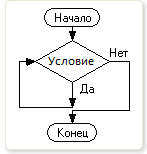 Рисунок 9 Источник 7 Пример. Найти факториал числа N. Пусть F - переменная, накапливающая факториал, R - число, меняющееся от 1 до N. Тогда F=1*2*3*...*N или F=R*(R+1)*(R+2)*...*N 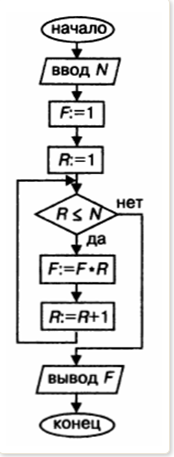 Рисунок 10 Источник 7 Цикл с полст-условием (до) Цикл с постусловием — цикл, в котором условие проверяется после выполнения тела цикла. Отсюда следует, что тело всегда выполняется хотя бы один раз.  Рисунок 11 Источник 7 Пример. Задача, в которой требуется вводить с клавиатуры числа и подсчитывать их сумму. Сумму необходимо подсчитывать до первого введенного отрицательного числа. Пусть S - сумма, A - вводимое число [Ист 7]  Рисунок 12 Источник 7 Понятие линейного алгоритма Изучив базовые структуры алгоритмов, можно рассказывать о самих алгоритмах. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами. Графическое представление алгоритмической конструкции в словестном виде «следование» приведено на рисунке:  Рисунок 13Источник 8 Линейный алгоритм приготовления отвара шиповника.  Рисунок 14Источник 8 Обратите внимание, что многие из предписаний этого алгоритма могут потребовать детализации — представления в виде некоторой совокупности более мелких предписаний. Пример в виде программной записи: У исполнителя Робот есть четыре команды перемещения (вверх, вниз, влево и вправо), при выполнении каждой из них Робот перемещается на одну клетку в соответствующем направлении. По команде закрасить Робот закрашивает клетку, в которой он находится. Запишем линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение:  Рисунок 15Источник 8 алг узор нач закрасить вправо вправо закрасить вниз влево закрасить вверх влево кон Где «алг» значит суть алгоритма, «нач»-начало, далее действия и «кон»-конец Пример в виде табличной записи: Дан фрагмент линейного алгоритма: x:=2 y:=x⋅x y:=y⋅y x:=y⋅x s:=x+y 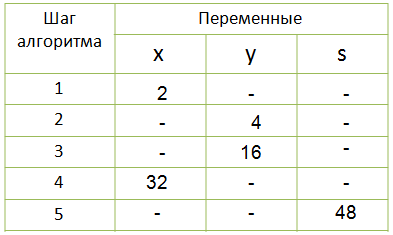 Рисунок 16 Источник 8 С помощью операции div вычисляется целое частное, с помощью операции mod — остаток. [Ист. 8]  Рисунок 17Источник 8 Понятие разветляющегося алгоритма Алгоритмы, в основе которых лежит структура «ветвления», называют разветвляющимися. Блок-схемы ветвления представлены на рисунках. Полная форма ветвления: 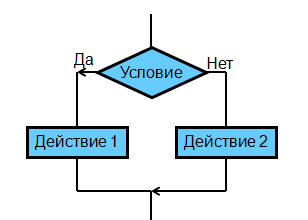 Рисунок 18 Источник 8 На программном языке команда ветвления записывается так:  Рисунок 19Источник 8 Ещё один пример:  Рисунок 20Источник 8 Неполная форма ветвления: 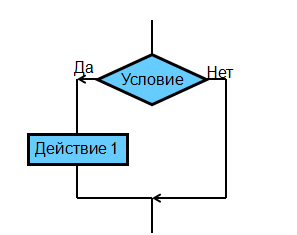 Рисунок 21Источник 8 На алгоритмическом языке команда ветвления записывается так:  Рисунок 22Источник 8 Ещё один пример:  Рисунок 23Источник 8 Для записи условий, в зависимости от результатов проверки которых выбирается та или иная последовательность действий, используются операции сравнения: A Здесь буквы A и B можно заменять на любые переменные, числа и арифметические выражения. Приведённые операции сравнения допускаются и для символьных переменных. Понятие цикличного алгоритма Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию повторения, называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла. В зависимости от способа организации повторений различают три типа циклов: цикл с заданным условием продолжения работы; цикл с заданным условием окончания работы; цикл с заданным числом повторений. Цикл с заданным условием продолжения работы. Логика работы этой конструкции описывается схемой, показанной на рисунке. 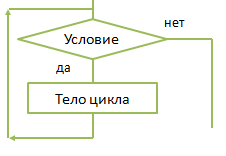 Рисунок 24Источник 8 На программном языке эта конструкция записывается так:  Рисунок 25 Источник 8 Выполняется цикл-ПОКА следующим образом: проверяется условие (вычисляется значение логического выражения); если условие удовлетворяется (Да), то выполняется тело цикла и снова осуществляется переход к проверке условия; если же условие не удовлетворяется, то выполнение цикла заканчивается. Возможны случаи, когда тело цикла не будет выполнено ни разу. Пример: алгоритм, по которому из всех имеющихся кирпичей отбираются целые кирпичи и складываются в машину.  Рисунок 26Источник 8 Пример: правее Робота расположен коридор неизвестной длины. Необходимо, чтобы Робот закрасил все клетки этого коридора. 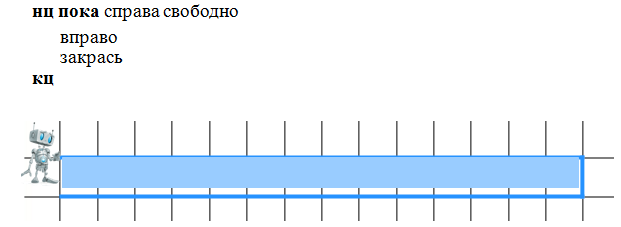 Рисунок 27Источник 8 Пример в виде блок-схемы:Требуется, не пользуясь операцией деления, получить частное q и остаток r от деления натурального числа x на натуральное число y. Представим операцию деления как последовательные вычитания делителя из делимого. Причём вычитать будем до тех пор, пока результат вычитания не станет меньше вычитаемого (делителя). В этом случае количество вычитаний будет равно частному от деления q, а последняя разность — остатку от деления r. 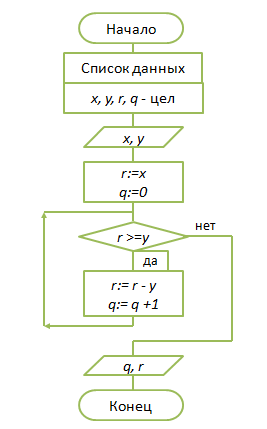 Рисунок 28Источник 8 Цикл с заданным условием окончания работы. Логика работы этой конструкции описывается схемой, показанной на рисунке. 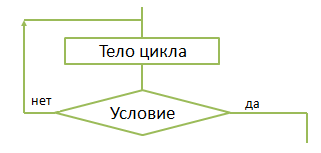 Рисунок 29Источник 8 На алгоритмическом языке эта конструкция записывается так: 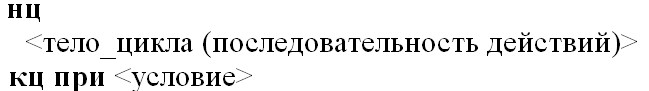 Рисунок 30Источник 8 Выполняется цикл-ДО следующим образом: выполняется тело цикла; проверяется условие (вычисляется значение логического выражения); если условие не удовлетворяется («Нет»), то снова выполняется тело цикла и осуществляется переход к проверке условия; если же условие удовлетворяется, то выполнение цикла заканчивается. В любом случае тело цикла будет выполнено хотя бы один раз. Пример: Алгоритм по выучиванию наизусть четверостишия.  Рисунок 31Источник 8 Пример: вычислим значение переменной b согласно следующему алгоритму: 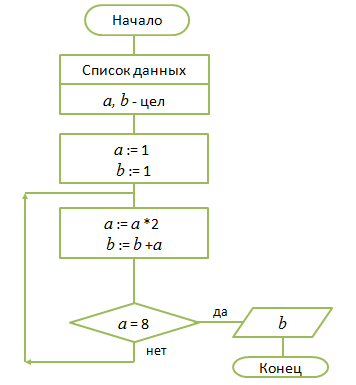 Рисунок 32Источник 8 Так же этот алгоритм в виде табличной записи: 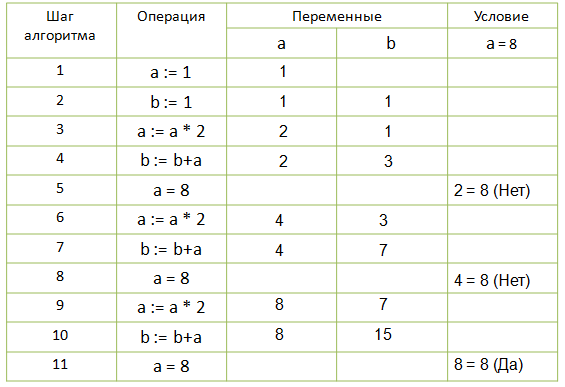 Рисунок 33Источник 8 Пример: Спортсмен приступает к тренировкам по следующему графику: в первый день он должен пробежать 10 км; каждый следующий день следует увеличивать дистанцию на 10 от нормы предыдущего дня. Как только дневная норма достигнет или превысит 25 км, необходимо прекратить её увеличение и далее пробегать ежедневно ровно 25 км. Начиная с какого дня спортсмен будет пробегать 25 км? Пусть x — количество километров, которое спортсмен пробежит в некоторый i-й день. Тогда в следующий (i+1)-й день он пробежит x+0,1x километров (0,1x — это 10 от x). 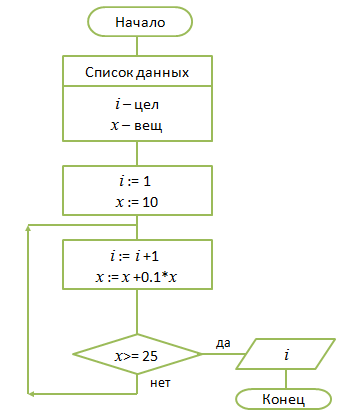 Рисунок 34Источник 8 Цикл с заданным числом повторений. Логика работы этой конструкции описывается схемой, показанной на рисунке. 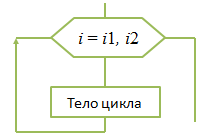 Рисунок 35Источник 8 На алгоритмическом языке эта конструкция записывается так:  Рисунок 36Источник 8 Важно понимать! В цикле-ДЛЯ всегда есть параметр цикла — величина целого типа, изменяющаяся в ходе выполнения цикла от своего начального значения i1 до конечного значения i2 с шагом R. Выполняется цикл-ДЛЯ следующим образом: параметру цикла присваивается начальное значение; параметр цикла сравнивается с конечным значением; если параметр цикла не превышает конечное значение, то выполняется тело цикла, увеличивается значение параметра цикла на шаг и снова осуществляется проверка параметра цикла; если же параметр цикла превышает конечное значение, то выполнение цикла заканчивается. Если величина шага в цикле с параметром равна единице, то шаг не указывают. Мы ограничимся рассмотрением именно таких циклов. В отличие от двух предыдущих конструкций (цикл-ПОКА, цикл-ДО) цикл-ДЛЯ имеет строго фиксированное число повторений, что позволяет избежать зацикливания, т.е. ситуации, когда тело цикла выполняется бесконечно. Пример: Алгоритм переправы через реку воинского отряда из пяти человек. Солдаты могут воспользоваться помощью двух мальчиков — хозяев небольшой лодки, в которой может переправиться или один солдат, или два мальчика.  Рисунок 37Источник 8 Для исполнителя Робот цикл с известным числом повторений реализуется с помощью следующей конструкции:  Рисунок 38Источник 8 Пример: Так, если правее Робота не встретится препятствий, то, выполнив приведённый ниже алгоритм, он переместится на пять клеток вправо и закрасит эти клетки:  Рисунок 39Источник 8 3.Зачем же нужны алгоритмы? Как можно было понять из описанного выше, с помощью алгоритмов возможно описать практически любое решение любой задачи, так же алгоритмы-фундамент для любой программы той или иной направленности. Я показал множество примеров их использования. Например, есть алгоритм заваривания чая или алгоритм сборки шкафа из ИКЕА. Но в контексте программирования мы имеем в виду другие алгоритмы. За всю историю компьютерных наук сложилось понимание, какие алгоритмы и структуры данных (способы их хранения) нужны для решения практических задач — так называемый джентльменский набор, который должен знать каждый разработчик. Например, сортировка: товары в магазине сортируют по стоимости или сроку годности, а рестораны — по удалённости или рейтингу. Хэш-таблицы помогают проверить корректность пароля и не хранить его на сайте в открытом виде, графы — находить кратчайший путь и хранить связи между пользователями в соцсетях. Все эти алгоритмы и структуры данных уже давно реализованы в библиотеках популярных языков программирования. Никто больше не пишет вручную алгоритм сортировки чисел, а чтобы пользоваться хэш-таблицами, даже не нужно знать, как они устроены. Разбираемся, зачем же нужны алгоритмы и в каких ситуациях их знание будет преимуществом. Знание алгоритмов помогает найти эффективное решение задачиПредставьте, что вам нужно сходить в магазин за продуктами. До него есть три дороги: вдоль проезжей части по хорошо освещённому тротуару (долго, но безопасно), дворами, где ездит много машин (быстро, но небезопасно), на трамвае (быстро, безопасно, но нужно платить). У этой задачи также могут быть и другие решения: доехать на машине, заказать доставку на дом или отправить за продуктами собаку. Аналогично и в программировании. Задача разработчика — использовать наиболее эффективное решение. Для этого нужно учитывать скорость работы программы, объём потребляемой памяти, экономическую эффективность (насколько стоимость решения оправдана конечным результатом), простоту реализации, масштабируемость. [Источник: София Техажева, руководитель программ «Python-разработчик» и «Алгоритмы для разработчиков» в Яндекс.Практикуме]. Заключение В данной курсовой работы я провел анализ структур алгоритмов, алгоритмов, объяснил их необходимость в алгоритмизации, показал примеры их использования и показал как они работают. | ||||||||||||||||||||||||||||||
