Курсовой Основы теории цепей. ОТЦ_Сх6.П1.ОИ.М4. Курсовая работа по дисциплине Основы теории цепей

• Название: Курсовая работа по дисциплине Основы теории цепей
• Анкор: Курсовой Основы теории цепей
• Дата: 11.03.2023
• Размер: 0.95 Mb.
• Имя файла: ОТЦ_Сх6.П1.ОИ.М4.doc
• Тип: Курсовая; #981386
• страница: 1 из 4

Министерство образования и науки Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра теоретических основ радиотехники (ТОР)

СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Курсовая работа по дисциплине

«Основы теории цепей»

Студент гр.142-1

_______Якимишин М.Э.

«____» ___________ 2004 г. Руководитель

Дмитриев В.Д.

«____» __________ 2004 г.

2004 г.

Реферат

Курсовая работа 36 с.,42 рисунка.

СХЕМНЫЕ ФУНЦИИ ЦЕПИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЦЕПИ, ПОЛОСА ПРОПУСКАНИЯ, ПОЛЮСНО-НУЛЕВОЕ ИЗОБРАЖЕНИЕ, ВХОДНОЕ СОПРОТИВЛЕНИЕ, РЕЗОНАНС.

Цель работы – овладеть способами нахождения частотных характеристик цепи.

2001 Professional Исследовать и получить входные и передаточные операторные функции нагрузки и транзистора (полевого) с нагрузкой. Произвести предполагаемый характер частотных характеристик. Научиться анализировать операторные функции цепи и овладеть для схем с зависимыми источниками методом узловых потенциалов. Рассчитать частотные характеристики (ЧХ) по выражениям АЧХ и ФЧХ, на основе карты нулей и полюсов (ПНИ) и при помощи автоматизированного метода анализа цепей проверить правильность вычислений.

Пояснительная записка к курсовой работе выполнена в текстовом редакторе Microsoft Word XP, с использованием MathCAD

СОДЕРЖАНИЕ

1 Введение 5

2 Исходные данные 6

3.Расчетная часть 7

3.1.Исследование нагрузки 7

3.1.1.Предполагаемый на основе схемы характер АЧХ и ФЧХ входной и передаточной функций: 7

3.1.2.Вывод операторных выражений входной и передаточной

функций 12

3.1.3.Нормировка операторных функций 14

3.1.4.ПНИ операторных функций 15

3.1.5.Расчет резонансных частот и резонансных сопротивлений 18

3.1.6.Определение ППЦ 19

3.2.Исследование транзистора с обобщенной нагрузкой. 20

3.2.1.Вывод операторных выражений на основе МУП 20

3.2.2.Нормировка операторных функций 22

3.3.Исследование транзистора с избирательной нагрузкой 23

3.3.1.Предполагаемый характер ЧХ 23

3.3.2.Получение выражений входной и передаточной функций 25

3.3.3.Предполагаемый ЧХ на основе ПНИ и ЧХ на =2 27

3.3.4.Выражения АЧХ и ФЧХ и ЧХ на 31

3.3.5.АЧХ и ФЧХ обеих функций на основе автоматизированного

расчета. 32

3.3.6.Входное сопротивление полной цепи в виде последовательной и параллельной модели 34

4.Вывод 35

Список использованной литературы 36
1. ВВЕДЕНИЕ

Комплексная функция цепи (КФЦ) есть отношение комплексной амплитуды отклика к комплексной амплитуде воздействия. Использование комплексных амплитуд свидетельствует о том, что цепь находится в установившемся режиме под гармоническим воздействием.

Все КФЦ принято делить на входные и передаточные. КФЦ называется входной, если воздействие и отклик принадлежат одной и той же паре полюсов: Z(iw), Y(iw); КФЦ называется передаточной, если воздействие и отклик принадлежат разным парам полюсов: K_u(iw), K_J(iw), Z_{l m}(iw), Y_{l m}(iw).

Двухполюсник (цепь с двумя полюсами) описывается только входными функциями. Трех-, четырех-, n- полюсник описывается как входной, так и передаточной КФЦ.

Любая КФЦ несет информацию, как об амплитудных, так и о фазовых соотношениях отклика и воздействия; поэтому любая КФЦ может быть представлена в виде двух характеристик: амплитудно-частототной (АЧХ) и фазо-частотной (ФЧХ).

АЧХ показывает закон изменения амплитуды отклика от частоты гармонического воздействия с неизменной амплитудой; математически АЧХ определяется как модуль КФЦ. ФЧХ показывает, как меняется фаза сигнала отклика относительно фазы сигнала воздействия при изменении частоты воздействия; математически ФЧХ определяется как аргумент КФЦ.

Общая методика получения выражения для частотных характеристики цепи состоит в следующем:

-получают выражение интересующей КФЦ,

-находят выражения АЧХ как модуль КФЦ,

-находят выражения ФЧХ как аргумент КФЦ.

Эта методика одинакова для цепей любой сложности.

КФЦ рассчитывается при неопределенном значении частоты любым удобным способом.

Несмотря на то, что ЧХ рассчитываются и экспериментально снимаются при гармоническом воздействии, ЧХ позволяют судить о поведении цепи при сложном воздействии как в установившемся, так и в переходном режиме.

Полоса пропускания цепи (ППЦ)- непрерывная область частот, в пределах которой значения АЧХ отличаются от своего максимального значения не более чем в раз или на 3 дБ.

ППЦ может быть определена как на основе графика АЧХ, так и на основе выражения для АЧХ.

Методика определения ППЦ на основе выражения АЧХ состоит в следующем:

-определяется максимальное значение АЧХ-K_max,

-выражение АЧХ приравнивается значению ,

(1.1)

-вычисляются значения граничных частот из равенства (1.1),

-находится полоса пропускания цепи.

2. ИСХОДНЫЕ ДАННЫЕ

Исходные данные курсовой работы:

Шифр: Сх6 П1 ОИ М4 ;

Параметры нагрузки: =100 Ом, m=0.4 ;

Частотные параметры: _max=4, N=0.05 ;

Нормирующие величины: R₀= , _ср (или _р)

• 
  Сх6- схема нагрузки №6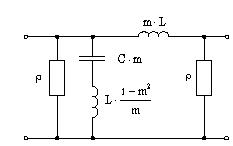
  

Рисунок 2.1 Модель избирательной нагрузки

• 
  OИ М4-модельполевого транзистора с общим истоком: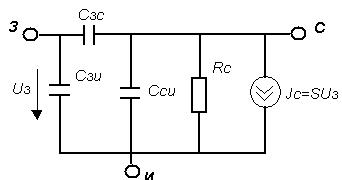
  

Рисунок 2.2 Модель полевого транзистора

• 
  П1- параметры полевого транзистора:
  

Сзи=4,8 пФ So=12.3

Сси=2.9 пФ Rc=980 Oм

Сзс=1.1 пФ

3. Расчетная часть

3.1 Исследование нагрузки

3.1.1: Предполагаемый на основе схемы характер АЧХ и ФЧХ входной и передаточной функции

• 
  Входная функция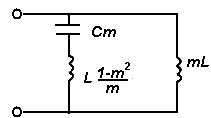
  

Рисунок 3.1. Модель избирательной нагрузки.

На рис. 3.1.представлен идеальный реактивный двухполюсник, в котором наблюдается 3 реактивных элемента. На рисунках 3.2 и 3.3 представлены схемы и диаграммы реактивных двухполюсников для параллельного и последовательного соединений элементов L и C.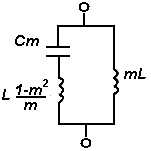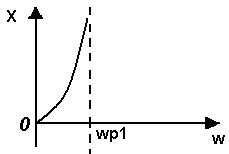



Рисунок 3.2 Параллельное соединение реактивных элементов

X(0)=0 (разрыв на С)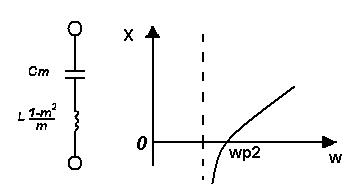

Х( )= (закоротка на С)


Рисунок 3.3 Последовательное соединение реактивных элементов

X(0)=- (разрыв на С)

Х( )= (разрыв на L)
На рисунке 3.4 изображена диаграмма реактивных сопротивлений Х( 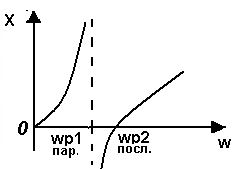) для полной схемы реактивного двухполюсника.


Число независимых реактивностей k=3, т.о. число возможных резонансов Np 2
Рисунок 3.4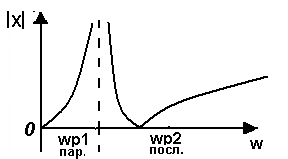



Рисунок 3.5 График модуля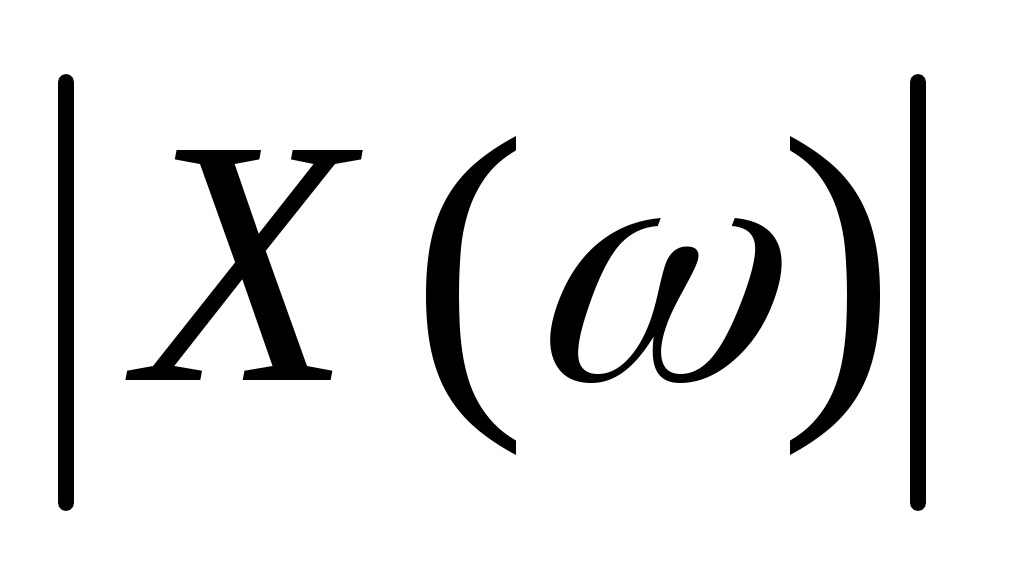

• 
  Расчет на крайних частотах диапазона входного сопротивления с учетом влияния сопротивлений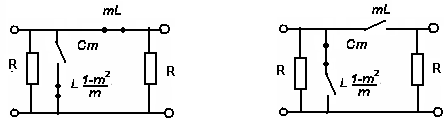
  

Z_ВХ(0)= , К(0)=1 Z_ВХ( )= ,К( )=0

Рисунок 3.6 Модели цепей на крайних частотах

На схема представляет собой параллельное соединение двух одинаковых сопротивлений. При ток протекает по пути меньшего сопротивления, т.е. через сопротивление на входе, на индуктивностях в этот момент происходит разрыв.
Рассмотрим моменты, когда _рез.

Z_вх( _{рез.пар})= Z_вх( _резпос)=0

Рисунок 3.7 модели цепей на резонансных частотах

На рисунке 3.7 Представлены модели нагрузок на резонансных частотах. В пашей нагрузке будет наблюдаться 2 резонанса. Исходя из теоремы Фостера и рис.3.2, первым наступит параллельный резонанс. Однако он будет слабо выражен, т.к.сопротивление будет шунтировать параллельный контур, находящийся в резонансе.

• 
  АЧХ входной функции.
  

На основе проделанных действий построим на рисунке 3.8 предполагаемый характер АЧХ для входного сопротивления: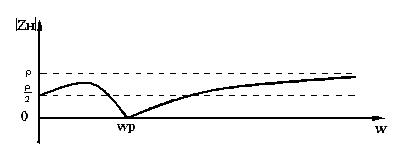




Рисунок 3.8

• 
  ФЧХ входной функции
  

Для определения ФЧХ входной функции воспользуемся диаграммой реактивностей на рисунке 3.4, а затем учтем влияние потерь.В соответствии с диаграммой X() ФЧХ реактивного двухполюсника имеет вид, представленный на рисунке 3.9.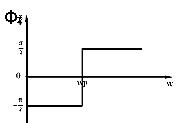



Рис 3.9 ФЧХ реактивного двухполюсника

Приведем схемы на крайних частотах рисунок 3.10 w0, рисунок 3.11 w∞: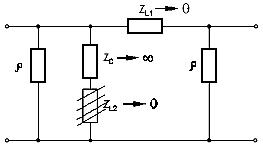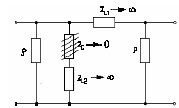



Рисунок 3.10 Рисунок 3.11
В результате таких действий становится очевидным, что Zвх при 0 определяется параллельным соединением  и , т.е. z(0)=0⁰, а при ∞ Zвх определяется , т.е. z(∞)=0⁰. Учитывая, что последовательный резонанс в схеме идеальный (нет потерь в последовательном контуре), ФЧХ на р изменяется скачкообразно.

Построим предполагаемый характер ФЧХ входной функции: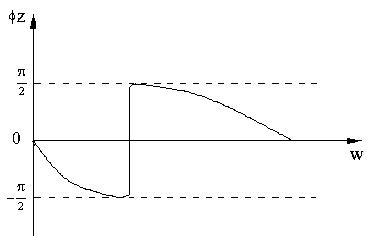



Рисунок 3.12 Предполагаемый характер ФЧХ входной функции.

• 
  Расчет на крайних частотах диапазона передаточной функции с учетом влияния сопротивлений
  

Представим исходную схему в виде П-образной модели и сделаем предположение о передаточной функции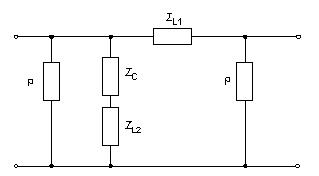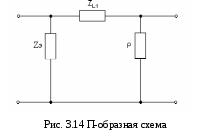




рисунок 3.13 Исходная схема

Очевидно, что коэффициент передачи К= 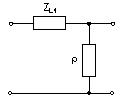не зависит от эквивалентного сопротивления Zэ. Таким образом, для нахождения коэффициента передачи достаточно рассмотреть часть схемы на рисунке 3.14., соответствующая сопротивлениям Z_L1 и  на схеме 3.15.



Рис. 3.15 Схема для определения характера передаточной функции

1. 
   w=0 (рисунок 2.8) Ku(j0)=1; Ku(0)= 1; _k(0)=0⁰
   
2. 
   w= (рисунок 2.9) Ku(j)=0;_k()=-90⁰;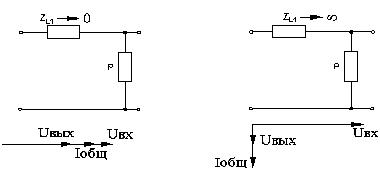
   

Рисунок 3.16 Рисунок 3.17
Построим предполагаемый характер АЧХ и ФЧХ передаточной функции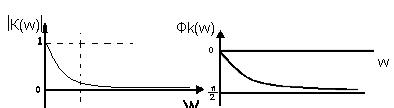


Рисунок 3.18 Предполагаемый характер АЧХ и ФЧХ передаточной функции.
3.1.2 Вывод операторных выражений входной и передаточной функций и их проверка по размерностям.

Проведем расчет операторных выражений по методу узловых потенциалов (МУП).

Представим схему избирательной нагрузки (рис.1.1) через схему проводимостей с зависимым источником Iпр.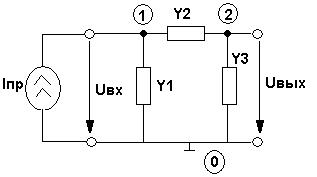




Рисунок 3.19 Схема нагрузки по МУПу

Y₁= =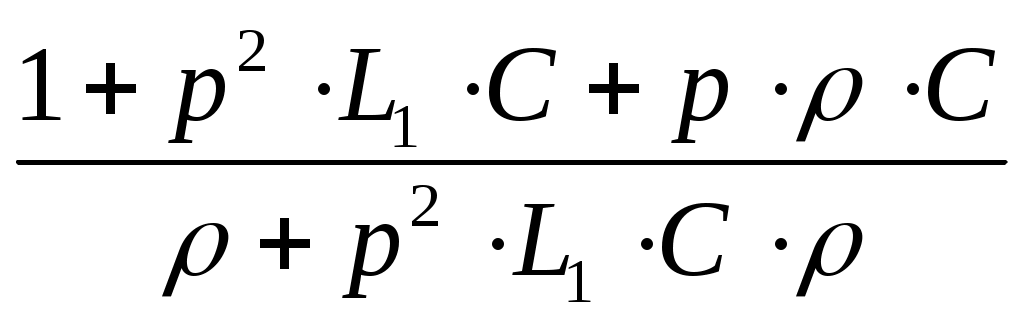
Y₂= Y₃=

Представим математическую модель цепи (ММЦ) в матричном виде: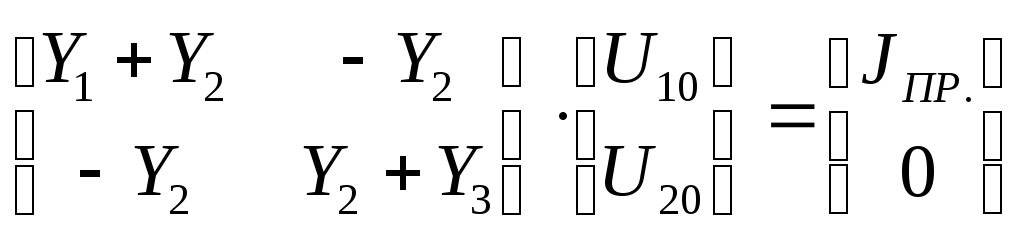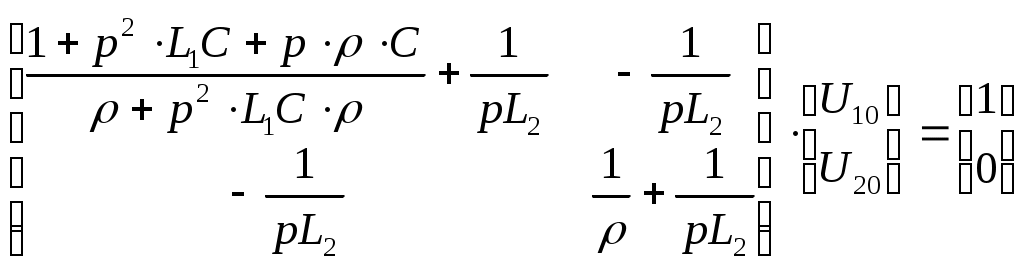

• 
  Входное сопротивление цепи Z_ВХ таким образом имеет вид: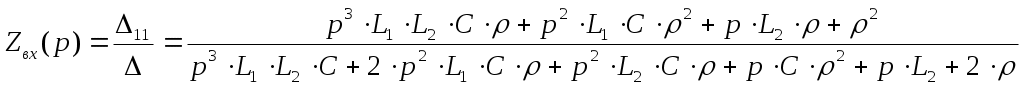
  

Произведем проверку:

1. по размерности: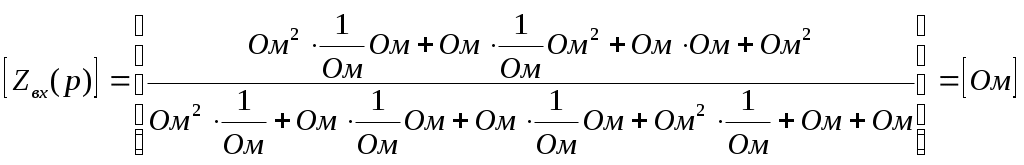



2 .проверка на крайних частотах: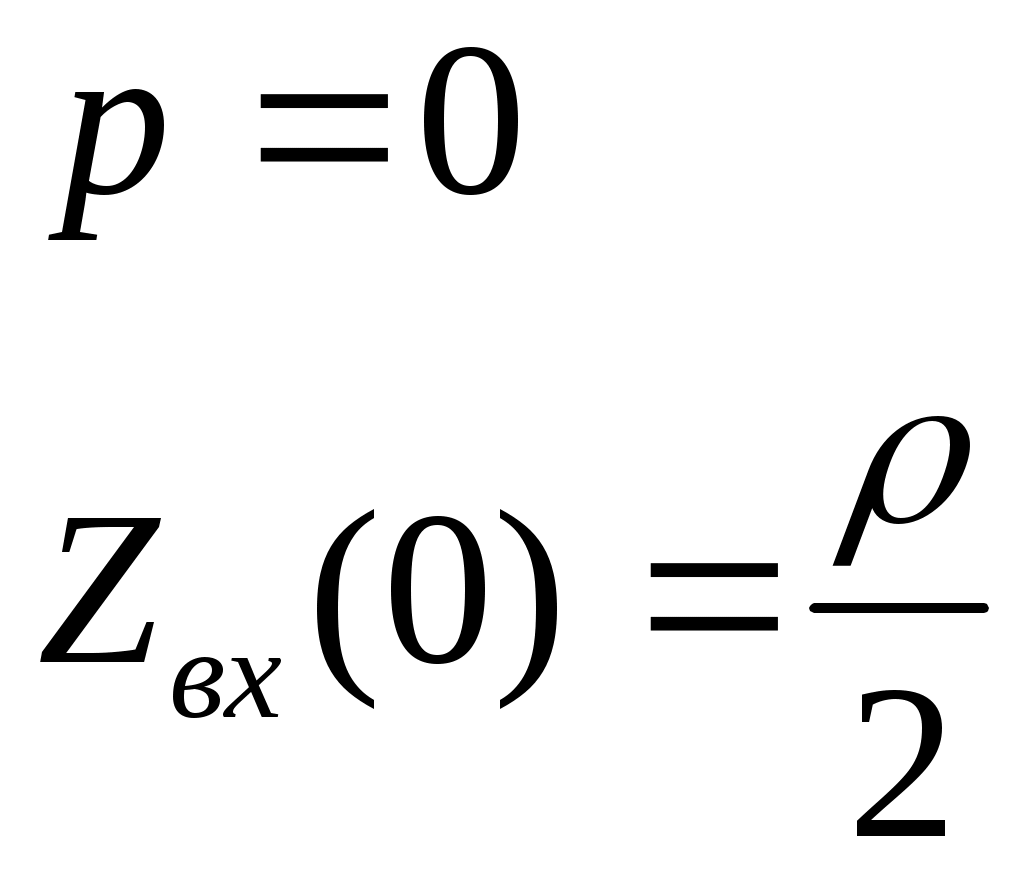



3. определение максимальной степени полинома функции Z_вх(p)





В схеме имеется 3 реактивных элемента. При подключении источника тока должно образоваться индуктивное сечение, но т.к. на входе присутствует шунт сечения не образуется. Емкостных контуров при подключении источника э.д.с. не образуется.

• 
  Передаточная функция:
  

Произведем проверку:

1. 
   проверка по размерности:
   

2. 
   проверка на крайних частотах:
   

3. числитель входной функции и знаменатель передаточной функции совпадают с точностью до общего множителя.
Условия физической реализуемости схемы:

1. 
   Максимальная степень числителя Ku_т(p) меньше его максимальной степени знаменателя при w0 K(p)0.
   
2. 
   Числитель Zвх(p) равен знаменателю Ku(p) с точностью до общего множителя (pL1+).
   
3. 
   Знаки всех слагаемых одинаковы и присутствуют все степени слагаемых без пропуска.