Курсовой Основы теории цепей. ОТЦ_Сх6.П1.ОИ.М4. Курсовая работа по дисциплине Основы теории цепей
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Нормировка операторных функций цепи. • Ненормированные значения. • Нормирующие значения • Нормировка. Таблица 3.1
Нормированные функции: Подставим нормированные значения функций в выражения входной и передаточной функций и получим: Входная функция 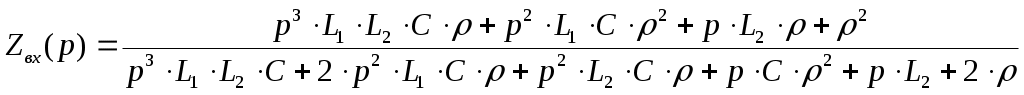 Передаточная функция: 3.1.4 Предполагаемый характер частотных характеристик (ЧХ) на основе ПНИ операторных функций и вычисление значений ЧХ на Входная функция: Н 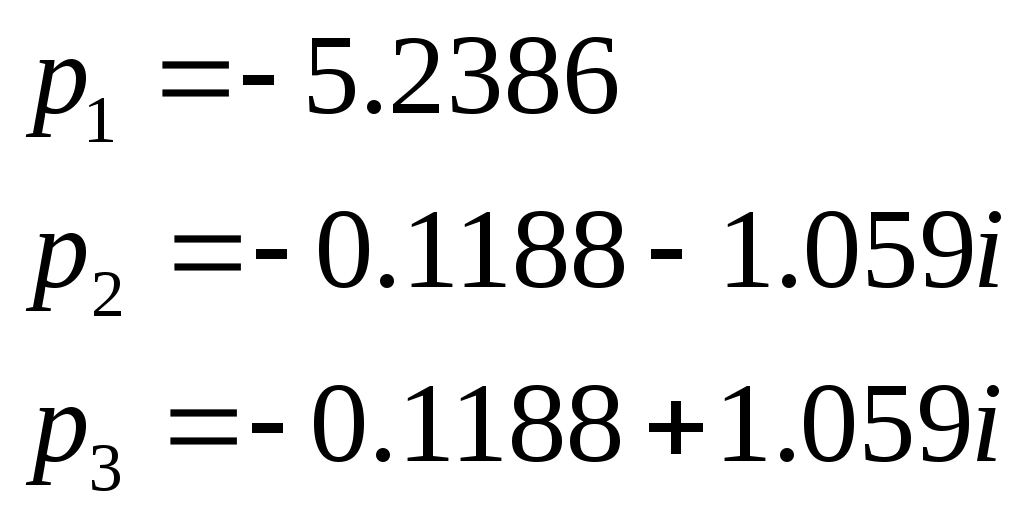 ули: Полюса: ули: Полюса: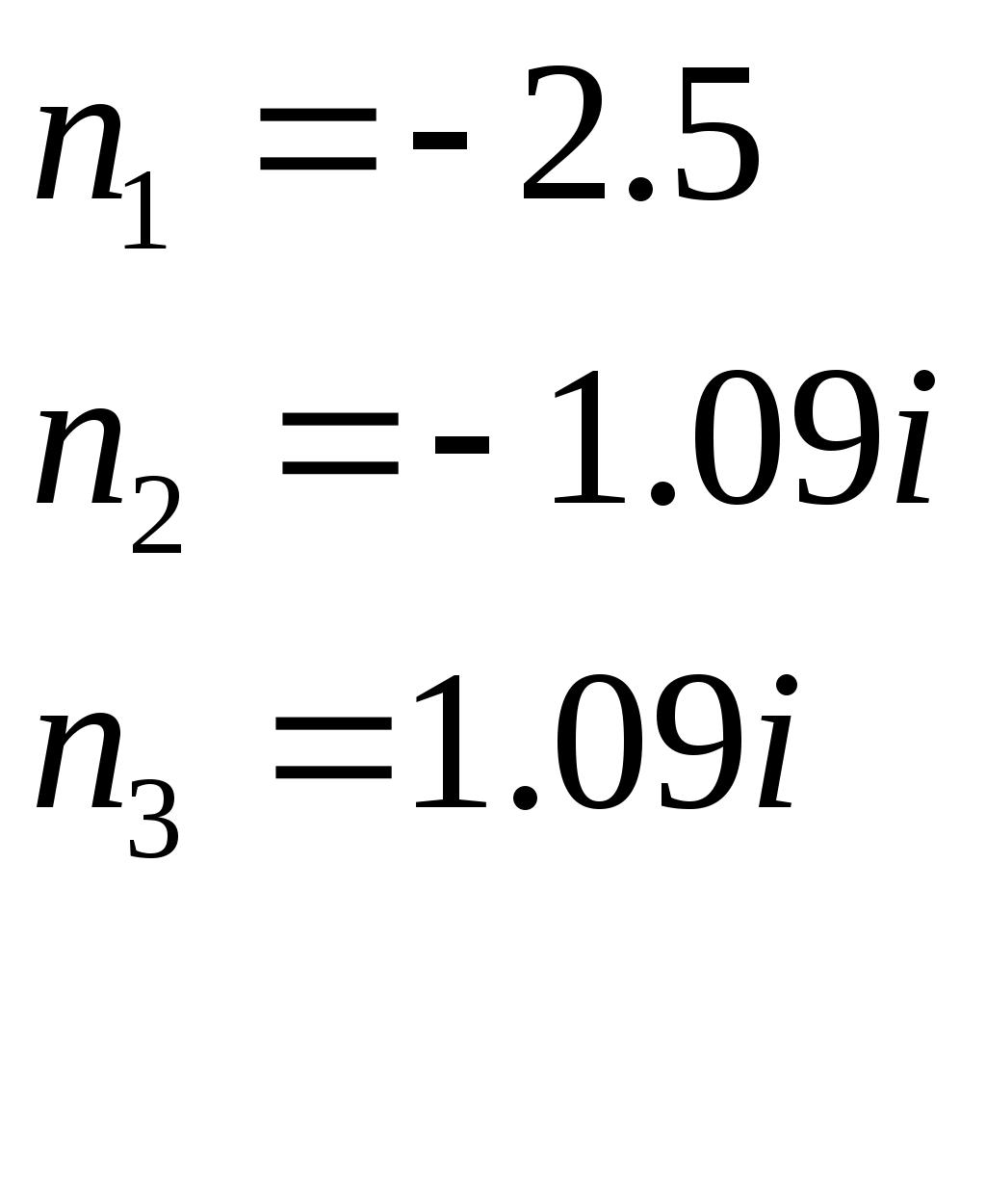 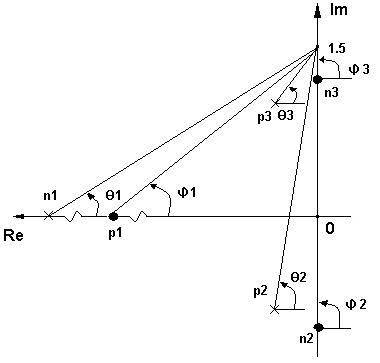 Рисунок 3.20 Карта нулей и полюсов входной функции Ниже в таблицах 3.2 и 3.3 приведены значения длин векторов и значения углов этих векторов соответственно для Таблица 3.2 значений длин векторов
Таблица 3.3 значений углов векторов
Расчет значений АЧХ ФЧХ производится по формулам: АЧХ: ФЧX: На АЧХ: ФЧХ: Для полной картины характера АЧХ и ФЧХ рассмотрим случай на крайних частотах по ПНИ. Имеем, что На АЧХ: ФЧХ: Построим в MathCad АЧХ и ФЧХ нормированной входной функции и сравним с предполагаемым характером ЧХ и тем, что мы получили по ПНИ. На рисунке 3.21 приведен модуль входного сопротивления, а на рисунке 3.22 фаза 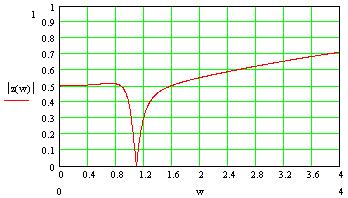 Рисунок 3.21 АЧХ входной функции 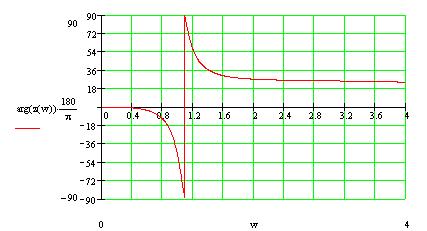 Рисунок 3.22 ФЧХ входной функции Из графиков видно, что предположения о характере ЧХ и вычисленные по ПНИ значения ЧХ на крайних частотах оказались верны. Так же совпадает расчет по ПНИ на заданной частоте Передаточная функция: У этой функции нет нулей, поэтому цепь – фазонеминимальна. Имеется только один полюс p=2.5. Таким образом мы можем с легкостью получить значения коэффициента передачи на заданной и крайних частотах. На АЧХ: ФЧХ: На АЧХ: ФЧХ: Построим в MathCad АЧХ и ФЧХ нормированной передаточной функции и сравним с предполагаемым характером ЧХ и тем, что мы получили по ПНИ. На рисунке 3.23 приведен модуль коэффициента передачи, а на рисунке 3.24 фаза 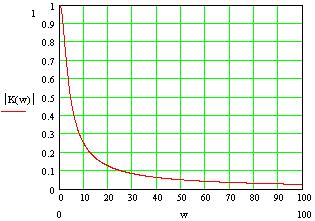 Рисунок 3.23 АЧХ передаточной функции 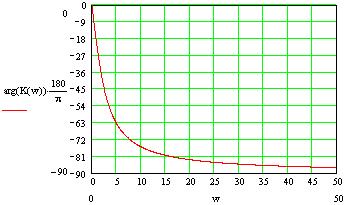 Рисунок 3.24 ФЧХ передаточной функции Схема избирательной нагрузки является фазоминимальной, потому как в правой полуплоскости отсутствуют у 3.1.5 Расчет резонансных частот и сопротивлений. Вычисление резонансных частот и сопротивлений проводится на основе нормированного выражения Выделим действительную и мнимую части входного сопротивления: Определение резонансной частоты Резонанс наступит в цепи, когда Из всех корней нас удовлетворяет только последний Определение резонансного сопротивления Rp Необходимое сопротивление можно найти подстановкой В ненормированном виде сопротивление резонанса выглядит следующим образом 3.1.6 Определение полосы пропускания цепи (ППЦ) Исследуем выражение АЧХ передаточной функции на экстремумы. Находим частоты, на которых она принимает наибольшие значения. АЧХ передаточной функции в нормированном виде Решение этого уравнения показало, что коэффициент передачи максимален тогда, когда Найдем граничную частоту: Таким образом, граничная частота равна : ППЦ будет равна: ППЦ(Н)= В ненормированном виде ППЦ: ППЦ= 3.2. Исследование транзистора с обобщенной нагрузкой. 3.2.1. Вывод операторных выражений на основе МУП и проверка полученных выражений всеми возможными способами. 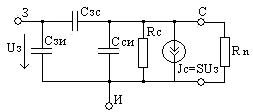 Рисунок 3.25 Схема транзистора с обобщенной нагрузкой. Представим транзистор (рис.3.24) через схему проводимостей с пробным источником. 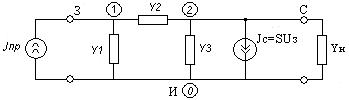 Рисунок 3.26 Схема транзистора в МУП. Запишем ММЦ в матричной форме. 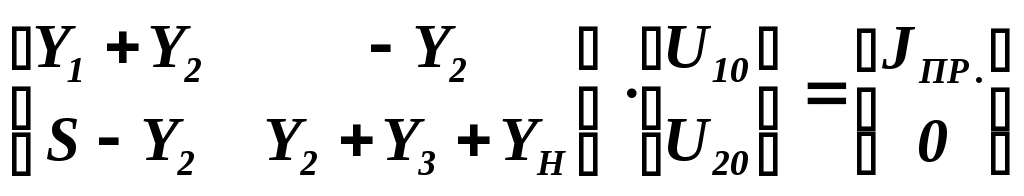 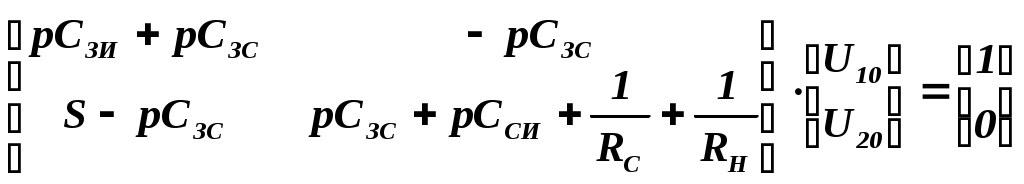 Входное сопротивление транзистора: Проверка: 1. Размерность. 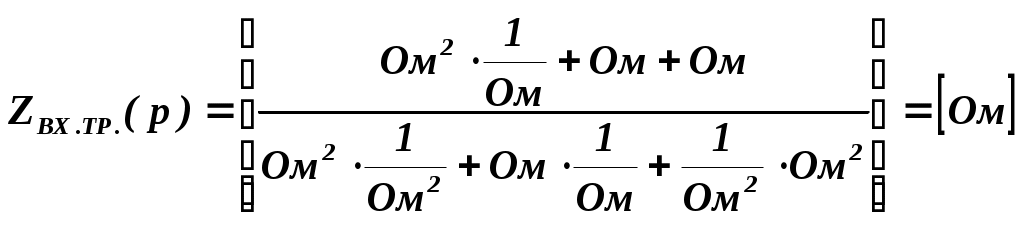 .2. Крайние частоты.   рис.3.27 Схема транзистора на крайних частотах 3. Порядок. При При Передаточная функция: Проверка: 1. Размерность. 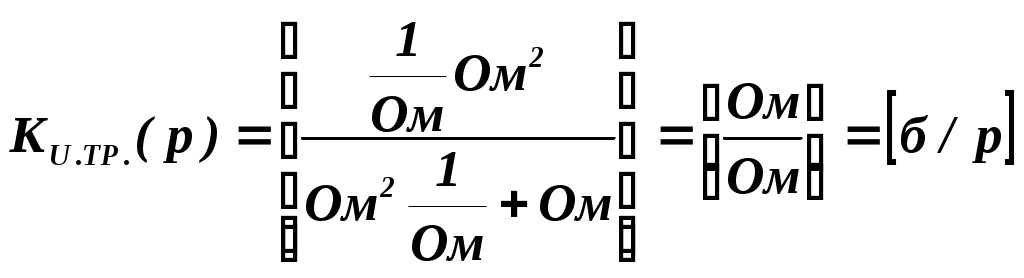 2. Крайние частоты. Проверку на нулевой частоте для транзистора проводят сравнивая полученное выражение на Видно, что на На бесконечно большой частоте известно, что |
