Курсовой проект по ОТЦ Схемные функции и частотные характеристики линейных электрических цепей. Курсовой_ОТЦ_26 вар (Сх13.Т9.ОБ.М2). Курсовая работа "Схемные функции и частотные характеристики линейных электрических цепей"

• Название: Курсовая работа "Схемные функции и частотные характеристики линейных электрических цепей"
• Анкор: Курсовой проект по ОТЦ Схемные функции и частотные характеристики линейных электрических цепей
• Дата: 15.04.2021
• Размер: 0.6 Mb.
• Имя файла: Курсовой_ОТЦ_26 вар (Сх13.Т9.ОБ.М2).doc
• Тип: Курсовая; #194931

М инистерство образования

Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра теоретических основ радиотехники (ТОР)


Курсовая работа
"Схемные функции и частотные

характеристики линейных электрических цепей"


Вариант № 26


Выполнил студент

Проверил

Мельникова И.В.

2005 г.

СОДЕРЖАНИЕ

1. 
   Исходные данные 2
   
2. 
   Задание 2
   
3. 
   Расчетная часть
   
   1. 
      Исследование нагрузки 2
      
   2. 
      Исследование схемы транзистора с обобщенной нагрузкой Zн 15
      
   3. 
      Исследование транзистора с избирательной нагрузкой 19
      

4. Литература 29
Определение номера варианта.

N = (XX*K)div100 = (77*35)div100 = 26, где

XX – две последние цифры пароля;

К – общее количество вариантов.

1. ИСХОДНЫЕ ДАННЫЕ

Шифр ________Сх.13.Т9.ОБ.М2______________, К или Кт _______К______,

Параметры нагрузки _______ = 300 Ом_______, ___________m = 0,6_____,

Частотные параметры ______w^H_max = 3_________, ___________N = 0,05_____,

Нормирующие величины ___R₀ = , ω₀ = ω_р (или ω_ср) .

2. ЗАДАНИЕ

Получить и исследовать входные и передаточные операторные функции.

Рассчитать частотные характеристики (ЧХ) по выражениям АЧХ и ФЧХ, на основе карты нулей и полюсов и с использованием автоматизированных методов анализа цепей.

3. РАСЧЕТНАЯ ЧАСТЬ
3.1 Исследование нагрузки.

М одель цепи.


Рис.1

где

R=ρ, , ,
Характер АЧХ и ФЧХ входной (Z_вх) и передаточной (К)функции.
Входная функция.

Изобразим эквивалентные схемы цепи на крайних частотах, и на частотах резонанса.



Z(0) = R Z(∞) = R/2
а) б)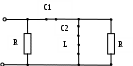




в) г)
Рис.2
Т.к. R шунтирует вход, то |Z_вх | ≤ R на любой частоте.
В результате анализа можно предположить, что АЧХ входной функции (|Z_вх|) имеет вид:




Рис.3
АЧХ передаточной функции К(ω).
Исследуемая цепь имеет П- образную структуру:



Рис.4

очевидно, что коэффициент передачи не зависит от значения Z1, и определяется только сопротивлениями Z2 и Z3. Поэтому, для нахождения К(ω) рассмотрим часть схемы соответствующую сопротивлениями Z2 и Z3.




Рис.5
Рассмотрим данную схему на крайних частотах и при частотах резонанса: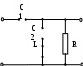


ω = 0 ω = ∞

К(0) = 0 К(∞) = 1
а) б)






ω = ω_р1 ω = ω_р2
К(ω_р) = 0 К(ω_р) > 1
в) г)

Рис.6

В данной схеме возникает два резонанса. Первый, на частоте ω_р1, последовательный контур C₂L, рис. 6,в. Далее, по мере увеличения частоты, сопротивление контура C₂L приобретает индуктивный характер Х_Lэ. Поэтому на частоте ω_р2 возникает второй резонанс, в последовательном контуре С₁Х_Lэ, рис. 6,г. А т.к. выходное напряжение снимается в том числе и с Х_Lэ, то на данной частоте выходное напряжение (резонансное) превышает входное напряжение и коэффициент передачи > 1.
В результате анализа можно предположить, что АЧХ передаточной функции К(ω) имеет вид:


Рис.7
Для определения ФЧХ φ_z необходимо сохранить тип реактивных сопротивлений, т.е.:
при ω→0 |Z_C|→∞ , |Z_L|→0

при ω→∞ |Z_C|→0, |Z_L|→∞
На крайних частотах Z_ВХ определяется R, значит φ_z(0) = 0^o; φ_z(∞) = 0^o.

На частотах 0 < ω < ω_р2, φ_z определяется Z_C1 и стремится к -90^о, но из-за шунтирующего действия R, не достигает максимального значения.

При переходе через резонансную частоту ω_р2, ФЧХ стремится к нулю, но из-за наличия потерь происходит это не скачкообразно, а плавно.

Далее, при увеличении частоты, на ФЧХ оказывает влияние Z_L, определяя ее в положительной области, но незначительно, пока |Z_L| < R.

В результате анализа можно предположить, что ФЧХ входной функции φ_z имеет вид:



Рис.8
Определение ФЧХ передаточной функции φ_К.
Т.к. , то .

Пологая , имеем
Для определения ФЧХ передаточной функции φ_К построим эквивалентные схемы на крайних частотах (неучитываемые сопротивления, на данной частоте, окрашены в темный цвет):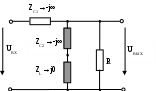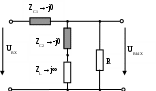



ω→ 0 ω→ ∞

φ_К(0) = +90^о φ_К(∞) = 0^о
а) б)

Рис.9

При ω→ 0 ток определяется |Z_C1|, φ_К(0) = +90^о .

При 0 < ω < ω_р1 ток определяется |Z_C1| и |Z_C2|.

При подходе к ω_Р1 с права, фазы токов |Z_C1| и |Z_C2| взаимно компенсируются φ_К → 0.

При переходе частоты ω_Р1, |Z_L| < R , и φ_К определяется токами |Z_C1| и |Z_L|, которые синфазные, при этом φ_К получает скачком приращение + 180⁰.

На резонансной частоте ω_р2 , ФЧХ определяется Х_Lэ, при этом φ_К = +90^о.

Далее, при ω > ω_р2, ФЧХ плавно спадает до нуля.
В результате анализа можно предположить, что ФЧХ φ_К имеет вид:




Рис.10
Вывод операторных выражений входной и передаточной функций и их проверка по размерности, соответствию модели на край них частотах диапазона, порядку полиномов и условиям физической реализуемости.
Операторные функции формально получаются из комплексных, заменой jω на оператор р:



Итак, для исследуемой цепи выводим выражения Z_ВХ(р) и К(р).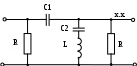


а) б)

Рис.11

,



Проверка размерности:

Учитывая, что , то размерности слагаемых полинома:

.
На крайних частотах при р = 0 и р = ∞ (после раскрытия неопределенности) выражение дает значения:

,

.
Это соответствует анализу схемы при ω = 0, ω = ∞.


Определение максимального порядка полиномов.
До подключения и после подключения на вход источника э.д.с. и источника тока, емкостные контуры и индуктивные сечения отсутствуют, значит:

,
это соответствует тому, что при ω = ∞ Z_ВХ определяется элементом R.
Соотношения минимальных степеней полиномов так же n = m, что соответствует Z(0)=R.

Вывод выражения К(р).



а) б)

Рис.12

.

.

.

.
Проверка по размерности.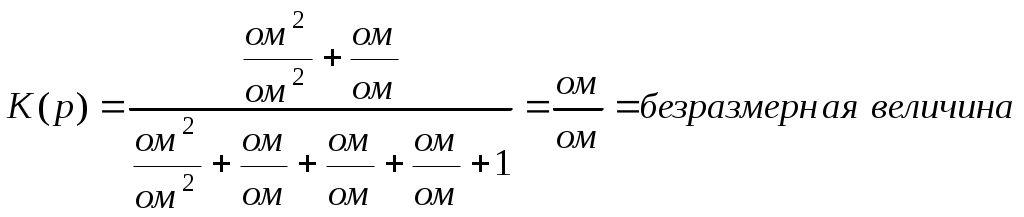

.
Проверка на крайних частотах.
при р = 0 К(р) = 0,

при р = ∞ К(р) = 1.
Это соответствует анализу схемы при ω = 0, ω = ∞.
Ограничение на соотношения степеней числителя и знаменателя передаточной функции не устанавливается.
Нормировка операторных функций.
Нормировка по частоте:
Находим нормирующую частоту ω₀.
ω₀ = 2π f_cp.

f_cp = N·f_гр.

f_гр = f_a ≈ 1.41· f_T,

где

f_T = 300 МГц,

N = 0.05,

тогда

f_гр = f_a = 423 МГц,

f_cp = N·f_гр = 21,15 МГц,
ω₀ = 2π f_cp =132,89 ·10⁶ рад/с
, р^н = j·ω^н.
Нормировка по сопротивлению:
.
Нормированные параметры:

L^(H) =1

C^(H) = 1

тогда из исходной схемы

,

,

.
Подставляя нормированные значения в формулы для Zвх(р) и К(р) получим:
,
.


Предполагаемый вид частотных характеристик (ЧХ) на основе карты нулей и полюсов и вычисление ЧХ на ω^н = 0,5.

Расчет нулей и полюсов ведем на основе нормированных выражений.

Нули функции – корни полинома числителя, полюса функции – корни полинома знаменателя.

,

где значение в каждой скобки выражения, в общем случае, комплексное число вида , следовательно

,

откуда

АЧХ:

ФЧХ:
В дальнейшем, для упрощения и наглядности, знак нормировки опускаем.
Полюсно-нулевое изображение (ПНИ) входной функции.
Находим нули и полюса функции из выражения для :

.

Z₀ = 0,5

р₀₁ = -0,416; р₀₂ = -0,092 + j0,957; р₀₃ = -0,092 - j0,957.

р_П1 = -0,263; р_П2 = -0,169 + j0,838; р_П3 = -0,169 - j0,838.
С 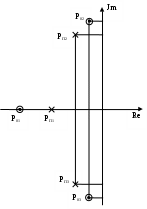троим карту полюсов и нулей.

ω₀₂
ω_П2


Рис.13
Анализ АЧХ, при изменении частоты от ω = 0 к ω = ∞ (вверх по мнимой оси).
Z(0) = const, т.к. в начале координат нет ни нуля, ни полюса.

Z(в области ω_П2) ≈ max, т.к. модуль П₂ принимает наименьшее значение.

Z(в области ω₀₂) ≈ min, т.к. модуль М₂ принимает наименьшее значение.

Z(∞) определяется соотношением максимальных степеней числителя и знаменателя, поэтому в нашем случае Z(∞)→ Z₀ = 0,5.
Анализ ФЧХ.
φ_Z(0) = 0^о, т.к. ни нуль, ни полюс не лежат в начале координат.

Т.к. полюс р_П2 лежит достаточно близко к мнимой оси, то в области этой точки φ_Z имеет отрицательное значение.

При переходе через точку р₀₂ (лежащую очень близко к мнимой оси) входная функция плавно меняет фазу с минуса на плюс.

φ_Z(∞) определяется Z₀, т.к. оно положительно то φ_Z(∞) = 0^о.
Предположительно АЧХ и ФЧХ входной функции имеет вид: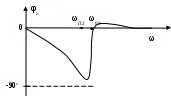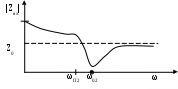






АЧХ ФЧХ
а) б)

Рис.14


Полюсно-нулевое изображение (ПНИ) передаточной функции.
Находим нули и полюса функции из выражения для :
.
К₀ = 1

р₀₁ = 0; р₀₂ = j0,8; р₀₃ = - j0,8.
р_П1 = -0,417; р_П2 = -0,092 + j0,957; р_П3 = -0,092 - j0,957.
Строим карту полюсов и нулей.



Рис.15
Анализ АЧХ при изменении частоты от ω = 0 к ω = ∞ (вверх по мнимой оси).
К(0) = 0, т.к. в начале координат лежит нуль функции р₀₁.

К(р₀₂) =0, т.к. модуль М₂ обращается в нуль.

К(р_П2) ≈ mах, который выражен достаточно ярко, т.к. |Re(p_П2)|<< |Jm(p_П2)|

К(∞) определяется соотношением максимальных степеней числителя и знаменателя, поэтому в нашем случае К(∞)→ К₀ = 1.
Анализ ФЧХ.

φ_К(0) = +90^о, т.к. в начале координат лежит нуль функции р₀₁.

В промежутке 0< ω < ω(p₀₂), ФЧХ плавно спадает до нуля.

При переходе через точку р₀₂ (лежащую на мнимой оси) φ_К скачком получит приращение +180^о.

В точке полюса П₂, φ_К = +90^о.

При ω→∞ φ_К(∞), по соотношению степеней полиномов, определяется К₀, т.к. оно положительно то φ_К(∞) = 0^о.
Предположительно АЧХ и ФЧХ передаточной функции имеет вид: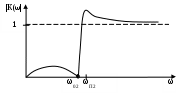



АЧХ

Рис.16
ФЧХ



Рис.17


Вычисление значений ЧХ на ω^н = 0,5.
Вычисление значения

входной функции Z_ВХ .



Рис.18

М1	М2	М3	П1	П2	П3
0,65	0,47	1,46	0,56	0,38	1,35

φ1	φ2	φ3	θ1	θ2	θ3
+50о	-78о	+86о	+62о	-64о	+83о

,

.


Вычисление значения передаточной функции при ω^н = 0,5.




Рис.19

М1	М2	М3	П1	П2	П3
0,5	0,3	1,3	0,65	0,47	1,46

φ1	φ2	φ3	θ1	θ2	θ3
+90о	-90о	+90о	+50о	-78о	+86о

Расчет резонансных частот и резонансных сопротивлений.
В соответствии с определением фазового резонанса на частоте ω_р входное сопротивление чисто активно и равно R_р:



,

Тогда



В дальнейшем, для упрощения и удобства, знак нормировки опускаем.
Z_ВХ(jω)=
Из мнимой части этого выражения находим нормированную резонансную частоту:



.

Полная резонансная частота равна:



Подставляя нормированную резонансную частоту в исследуемое выражение, получим нормированное резонансное сопротивление:


Определение полосы пропускания цепи.
Полоса пропускания цепи для четырехполюсников определяется по передаточной функции.



Т.к. исследуемый четырехполюсник является фильтром высоких частот, то его полоса пропускания от ω_гр до ∞,

где

.

Т.к. в передаче сигнала участвуют разнотипные реактивности, то |K(ω^н)|max находим путем исследования на экстремум:


,

при этом |K(ω^н)| = 1,667.

Из данного выражения находим ω^н_гр:
ω^н_гр= 0,934.

Ненормированное значение

ω_гр= ω^н_гр· ω₀ = 0,934·132,89 ·10 ⁶ = 124,12·10 ⁶ рад/с,

или

f_гр =19,75 МГц.

3.2 Исследование схемы транзистора с обобщенной нагрузкой.

М 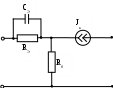одель транзистора .

Рис.20
Тип транзистора – n-p-n.

Способ включения – общая база.

Параметры:
Rэ = 27 ом; R_Б = 175,5 ом; Сэ =19,6 пФ; S₀ = 36,1 мА/В.
Определение схемных функций проводим с использованием метода узловых потенциалов (МУП).

Для реализации МУП на вход подключим пробный источник J_пр, рис. 21




Рис.21

Заменим сопротивления элементов их проводимостью
.
Запишем типовую систему для данной схемы:

Выразим зависимый источник через узловые напряжения
, где S - проходная характеристика транзистора.
Подставим данное выражение в исходную систему и приведем подобные по узловым напряжениям: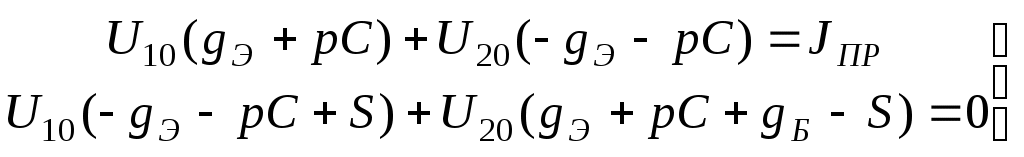

Для нахождения схемных функций систему представим в матричной форме:

По правилу Крамера: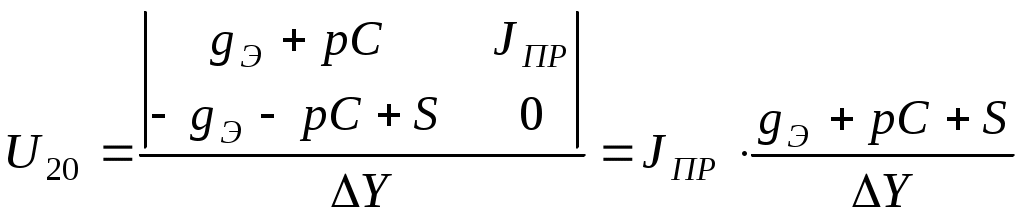
.
,
где ΔY – определитель матрицы проводимостей,
.
Искомые схемные функции имеют вид:


.


Проверка полученных выражений.


Размерность входной функции:

при р = 0, учитывая, что (g_э –S) →0, то Z_ВХ(0) = = R_Э (Ом),

при р = ∞ Z_ВХ = R_Б (Ом).
До подключения и после подключения на вход источника э.д.с. и источника тока, емкостные контуры и индуктивные сечения отсутствуют, значит:

,
Соотношение степеней полиномов равно - это соответствует R при ω = 0 и ω = ∞.
Размерность передаточной функции:

при р = 0, учитывая, что (g_э –S) →0, то К_Т = S·Z_H,

при р = ∞ К_Т = 0
Ограничение на соотношение степеней числителя и знаменателя передаточной функции не устанавливаются.
Нормировка операторных функций.
,

,

,
.
Подставляя численные значения, получим нормированные функции транзистора с обобщенной нагрузкой:


3.3 Исследование транзистора с избирательной нагрузкой.

Iвх

транзистор избирательная

Uвх Uт цепь (нагрузка) Uн


Рис.22
Kн = Uн/Uт, Kт = Uт/Uвх,
K = Uн/Uвх = Kт·Kн = S·Z_H·K_H
Нагрузкой транзистора является входное сопротивление избирательной цепи:



Рис.23
Предполагаемый характер АЧХ полной модели можно представить графически на основе формулы и графиков (рисунки 14,а и 16) соответственных функций, полученных ранее:
K = Kт·Kн = S·Z_H·K_H
|K| = |S|· |Z_H|·|K_H|

График для |S| взят из [1].



Рис.24
Получение нормированных выражений входной и передаточной функций полной цепи и их проверка на соответствие полиномов схемных функций, порядку полной цепи и соответствие минимальных и максимальных степеней функций значениям, полученным для полной схемы на крайних частотах.
Нормированное операторное выражение входной функции полной цепи совпадает с входной функцией модели транзистора:

Нормированное операторное выражение для передаточной функции полной цепи получим из ранее полученных нормированных выражений и формулы:




=


Проверка полученных схемных функций.

при р = 0 Z^н _ВХ(р) = 0,104

при р = ∞ Z^н _ВХ (р) = 0,59

Соотношение максимальных и минимальных степеней входной функции - что соответствует активному значению при ω= 0 ω = ∞.
при р =0 К^н(р) = 0,

при р = ∞ К^н(р) = 0.
Ограничение на соотношение степеней числителя и знаменателя передаточной функции не устанавливаются.

Предполагаемый характер ЧХ на основе карты нулей и полюсов и вычисление значений ЧХ на ω^н = 0,5.
Представим исследуемые функции в виде:




р₀₁ = -29

р_П1 = -163,8

Z ₀ = 0,59

Рис.25
Анализ карты нулей и полюсов для входной функции:
АЧХ Z_ВХ.
|Z_ВХ| (0) = const, т.к. ни нуль, ни полюс функции не лежит в начале координат.

А, используя формулу , легко представить |Z_ВХ| (0) на графике.

При ω = ∞, определяется соотношением максимальных степеней числителя и знаменателя, в нашем случае |Z_ВХ| (∞) → Z₀.
АЧХ входной функции предположительно имеет вид:


------------------------------------------------------------

Рис.26

ФЧХ Z_ВХ.
φ_Z (0) = 0, т.к. ни нуль, ни полюс функции не лежит в начале координат.

φ_Z (∞) = 0, при ω = ∞, (учитывая соотношения степеней полиномов) φ_Z определяется Z₀, т.к. оно положительно, то φ_Z = 0.
При 0 < ω < ∞ ФЧХ определяется формулой . Угол φ на начальном этапе отсчета, явно больше угла θ, поэтому график ФЧХ будет иметь вид:




Рис.27

Анализ карты нулей и полюсов передаточной функции:

К(р) =
р₀₁ = 0, р₀₃ = j0.8, р₀₃ = -j0.8
р_П1 = -29,1; р_П2 = -0,263; р_П3 = -0,169 + j0,839; р_П4 = -0,169 - j0,839.
К₀ = 12,57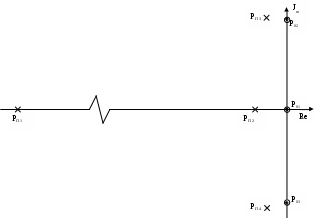



Рис. 28
Анализ карты нулей и полюсов для передаточной функции:
АЧХ.
К(0) = 0, т.к. нуль функции лежит в начале координат.

К(р₀₂) = 0, т.к. М₂ модуль превращается в нуль.

К(р_П3) = max, т.к. Re|K|<
К(∞) = 0, по соотношению максимальных степеней полиномов

ФЧХ.
φ_К (0) = +90^о, т.к. нуль функции лежит в начале координат.

При прохождении точки р₀₂ (лежащей на мнимой оси) φ_К скачком изменяет значение с

(-90^о) на (+90^о).

При прохождении точки р_П3 , где полюс близко расположен к мнимой оси, φ_К получает плавное приращение на (-180^о).

φ_К(∞) = -90^о, по соотношению максимальных степеней полиномов .
Примерный вид АЧХ и ФЧХ передаточной функции полной модели имеет вид: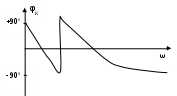






АЧХ ФЧХ


Рис.29


На основе карты нулей и полюсов произведем вычисления ЧХ на ω^н = 0,5.
Входная функция.
р₀₁ = -29

р_П1 = -163,8

Z₀ = 0,59



Рис.30
Очевидно без измерения, что модули нуля и полюса равны их численным значениям,

М₁ = 29; П₁ = 163,8. А углы φ₁ и θ₁ → 0.

Тогда:

|Z^н _ВХ|( ω^н = 0,5) = .

φ_Z ( ω^н = 0,5) ≈ 0⁰.

Передаточная функция.
р₀₁ = 0, р₀₃ = j0.8, р₀₃ = -j0.8
р_П1 = -29,1; р_П2 = -0,263; р_П3 = -0,169 + j0,839; р_П4 = -0,169 - j0,839.
К₀ = 12,57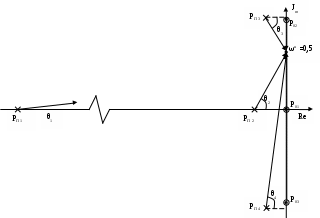


Рис.32

М1	М2	М3	П1	П2	П3	П4
0,5	0,3	1,3	29,1	0,57	0,37	1,34

φ1	φ2	φ3	θ1	θ2	θ3	θ4
+90о	-90о	+90о	0о	+62о	-60о	+81о

АЧХ. |K|( ω^н = 0,5) =
ФЧХ. φ_К ( ω^н = 0,5) = 0⁰ + (90 – 90 + 90) - (62 – 60 + 81) = 7^о.

Получение выражений АЧХ и ФЧХ обеих функций на основе нормированных выражений и расчет по ним значений ЧХ при ω^н = 0,5.

К(р^н) =
Заменяем р^н = j·ω^н и приводим выражения к виду:

АЧХ определяется как модуль функции |T|, а ФЧХ как ее аргумент φ_Т = ArgT.


|Z^н _ВХ|( ω^н = 0,5) = 0,104.


φ_Z ( ω^н = 0,5) = 0,81 ^о.





|Kω^н| ( ω^н = 0,5) = 0,293.

.
φ_К ( ω^н = 0,5) = 7,43 ^о.

Значения ЧХ обеих функций, при ω^н = 0,5, полученные двумя способами практически одинаковы.


Оценка устойчивости и фазоминимальности полной цепи, по карте нулей и полюсов.
Все полюсы и нули не находятся в правой полуплоскости, следовательно, цепь устойчива и фазоминимальна.
Ниже представлены характерные точки, АЧХ и ФЧХ полной цепи, в исследуемом диапазоне, ω^н_max = 3.

ωн	0	0,5	0,7	0,8	1	1,5	2	2,5	3
|K(ω)|	0	0,292	0,18	0	0,34	0,43	0,43	0,43	0,43
φkо	90	7,43	-25	125,5	64,4	25,5	15,2	9,8	6,1

АЧХ

Рис.33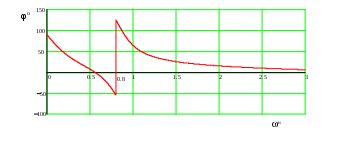




ФЧХ

Рис.34

Представление входного сопротивления полной цепи последовательной и параллельной моделями на одной из частот заданного диапазона (ω≠ 0 и ω≠ ω_р ).
Цепь любой сложности по отношению к входным зажимам выступает как двухполюсник с входным сопротивлением

,

а входная проводимость этого двухполюсника

,

Этим выражениям соответствует последовательная и эквивалентная параллельная модели входного сопротивления.
- представим данное выражение в виде a+jb, на ω^н = 0,5.
,
что соответствует нормированным активной и реактивной составляющей.

Реактивная составляющая соответствует емкостному сопротивлению.

Находим полные (ненормированные) значения:

Вместо нормированной частоты подставляем ненормированную, соответствующую

ω^н = 0,5.

ω=ω^н · ω₀ = 66,445 · 10⁶ рад/сек.
.






Эквивалентные схемы входного сопротивления:







R = 31,34 Ом С = 33,85 нФ R = 31,34 Ом С = 6,82 пФ
а) б)
Рис.35

4. ЛИТЕРАТУРА.

1. 
   Мельникова И.В. Основы теории цепей. Схемные функции и частотные характеристики линейных электрических цепей: Методические указания по выполнению курсовой работы. – Томск: Томский межвузовский центр дистанционного образования, 2001.-65 с.
   

2. 
   Мельникова И.В., Тельпуховская Л.И. Основы теории цепей. Часть 2: Схемные функции цепей. Резонансные цепи. Четырёхполюсники и LC-фильтры. Длинные линии: Учебное пособие – Томск: Томский межвузовский центр дистанционного образования, 2001.-186 с.
   

Рецензия.

Зачтено. Оценка «хорошо». Нет автоматизированного счета.

Рецензент: Мельникова И.В.