курсовая 11,2017. Курсовая работа по дисциплине Теория электрической связи Для специальности рэт

• Название: Курсовая работа по дисциплине Теория электрической связи Для специальности рэт
• Дата: 02.04.2019
• Размер: 227.23 Kb.
• Имя файла: курсовая 11,2017.docx
• Тип: Курсовая; #72308
• страница: 3 из 4

имеют амплитуду Е= const, поэтому они не могут быть продетектированы с помощью с помощью амплитудных детекторов, так как выходное напряжение этих детекторов зависит только от амплитуды модулированных колебаний.

Приведем еще структурная схема модулятора Армстронга для радиосигналов с угловой модуляцией (ЧМ- и ФМ- сигналоф). [1, с. 293, (рис. 11.10)]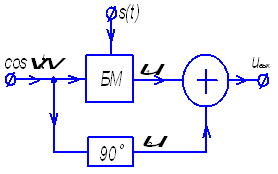


Рис. 5 Структурная схема модулятора Армстронга. [1, с.294,(рис. 11.10)]
Здесь к одному из входв сумматора приложен сигнал ν1, поступающий с балансного модулятора БМ. На второй вход сумматора подется немодулированный сигнал ν2 с выхода фазовращателя, изменяющего фазу гармонического сигнала несущей частоты на 900 в сторону запаздывания.

Ширина спектра ДМ сигнала зависит от ширины спектра модулирующего сигнала (прямоугольного видеоимпульса), определяемого длительностью видеоимпульса - ТТАКТ. Она определяется по упрощённой формуле:
FДОФМ = (23)/ТТАКТ = (23)∙FТАКТ, (Гц) (6.3)

FДОФМ =2∙88∙103 = 176∙103 (Гц)=176(кГц).



Алгоритм работы модулятора состоит в записи математических выражений первичных и соответствующих им передаваемых сигналов при передаче символов "1" и "0".

Алгоритм работы цифрового амплитудного модулятора приведён в таблице. 6.1.

Таблица 6.1.

Символ	Первичный сигнал UЦК(t) на входе модулятора	Вторичный модулированный сигнал S(t) на выходе модулятора
0	U0(t) = 0	S0(t) = U cos(0∙t )
1	U1(t) = UИМП	S1(t) = U cos(0 ∙t+φ)

Задание 7
Разработаем структурную схему демодулятора (детектора) и алгоритм его работы.

Детектирование ФМ колебаний может осуществляться либо с помощью синхронного детектора, либо путем предварительного преобразования их в колебания, амплитуда которых изменяется по закону модулирующего напряжения, с последующим амплитудным детектированием. В последнее время стали применяться также частотные детекторы на базе цифровых счетчиков частоты с цифроаналоговыми преобразователями (ЦАП).

Напряжение на выходе синхронного детектора
(7.1)
При ФМ колебании амплитуда Е постоянна, и выходное напряжение пропорционально , где - сдвиг фаз между входным ФМ напряжением и опорным немодулированным - напряжением. График зависимости выходного напряжения синхронного детектора от фазы входного ФМ напряжения представляет собой косинусоиду.

Синхронный детектор может быть использован для детектирования ФМ колебаний при условии, что фаза изменяется в пределах . Однако при изменении фазы в указанных пределах детектирование происходит с большими нелинейными искажениями.

Для ОФМ следует использовать фазовый демодулятор и устройство "внесения относительности". [4, п. 4.6]

Детектирование ЧМ и ФМ колебаний путем предварительного преобразования (Пр) их в колебания с амплитудой, изменяющейся по закону модулирующего сигнала, и с последующим амплитудным детектированием (АД) осуществляется в соответствии со структурной схемой на рисунке 7.1.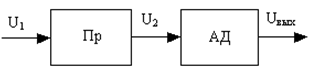


Рис. 7.1 Структурная схема детектора ФМ колебаний.

Преобразователь Пр преобразует колебание в колебание с изменяющейся амплитудой.
(7.2)
Выходное напряжение амплитудного детектора АД пропорционально амплитуде колебаний на его входе: .

Для детектирования ЧМ колебаний с малым индексом модуляции (m<1) применяется схема балансового фазового детектора с опорным напряжением (рис.7.2). Напряжение на выходе этого детектора зависит от разности фаз входного ФМ сигнала е и опорного напряжения ео, имеющего ту же несущую частоту, что и сигнал е: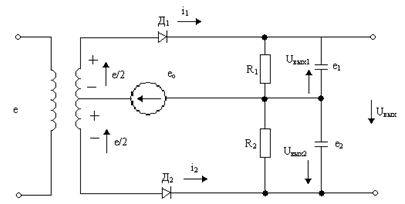
(7.3)

(7.4)


Рис 7.2. Схема балансового фазового детектора.
Схема приемника имеет вид: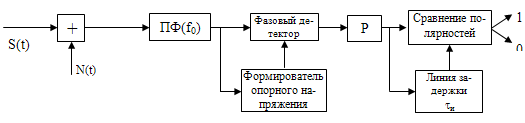



Рис. 7.3. Схема приемника ФМК.
Смесь сигнала и помехи поступает на полосовой фильтр (ПФ), настроенный соответственно на частоту с полосой пропускания равной ширине спектра ФМ сигнала. Затем происходит детектирование сигнала в фазовом детекторе и с выхода которого сигнал поступает на решающее устройство (Р). После него продетектированная посылка (0 или 1) сравнивается с предыдущей, задержанной с помощью линии задержки, на основании чего делается вывод о том, какой символ, 0 или 1, передавался.

Под действием помех в канале связи РУ может выносить неправильные решения, т.е. могут возникать ошибки первого и второго рода, т.е. p(0|1) и p(1|0). Помехоустойчивость системы характеризуется средней вероятностью ошибки:

ошср = P(0)P(1|0) + P(1)P(0|1) = Pош (7.5)
при равновероятных символах и ошибках первого и второго рода.


Задание 8
Определим величину параметра h2 на входе детектора, при которой достигается заданная вероятность ошибки Pош., если помеху, воздействующую на сигнал, считать "белым шумом" со спектральной плотностью мощности G0. Определим амплитуду сигнала, при которой достигается полученное значение h2.

Вероятность ошибки при оптимальном когерентном приёме равновероятных сигналов с ДАМ в канале с "белым" Гауссовским шумом, полученная в теории потенциальной помехоустойчивости, рассчитывается по формуле:

ош = 0,5 exp(-h2/2), (8.1)

где h2 = E/Go;

- энергия сигналов S1(t) и S0(t), (B2∙c);- спектральная плотность мощности помехи, (В2∙с) или (В2/Гц)

Отсюда:

= -2 ln(2 Pош). (8.2)= -2 ln(210-5) = 21,64
Для получения вероятности ошибки Pош =10-5, необходимо, чтобы величина h2 = 21,64

Мощность гармонического несущего сигнала:

= U2/2, (В2), (8.3)
где U - амплитуда сигнала, (B)

Энергия сигналов S1(t) и S0(t) равна:
Е = Рс TТАКТ, (B2∙c) (8.4)
Из формулы h2 = E/GO находим:

= h2 GO, (B2∙c) (8.5)

После подстановок и преобразований получим:
U =h2 GO/TТАКТ, (B) (8.6)
Или
U = h2 GO Fтакт, (B) (8.7)

U =  21,64 10-6 88 103 =2,69 (В)
Значение h2 = 21,64 достигается при амплитуде сигнала, равной U = 2,69 (В).
Задание 9
Вычислим вероятность неверного декодирования кодовой комбинации в декодере с учетом кодирования с проверкой на четность.

Кодовая комбинация, при условии использования кода с проверкой на четность, будет декодирована неверно, если будет принято с ошибкой четное количество символов.

Так как Pош<<1, то можно учитывать только вероятность ошибочного приёма двух элементов кодовой комбинации.

Тогда вероятность неверного декодирования кодовой комбинации, состоящей из n - элементов равна:
Рош К К = Р(2/n) = C2n P2ош  (1 - Рош )n-2 С2n P2ош (9.1)
где

Р(2/n) - вероятность двукратной ошибки в n- элементной кодовой комбинации;n - число сочетаний из n - элементов по 2 элемента ( показывает число возможных вариантов двукратной ошибки в n- элементной кодовой комбинации кода);

n = n!/ [2!  (n - 2)!] (9.1)

- длина кодовой комбинации помехоустойчивого кода.

ош К К n!/ [2!  (n - 2)!]  P2ош =11!/ [2!  (11-2)!]  (10-6) 2 =5510-12
Задача 10
Определим пропускную способность канала связи.

Для канала с постоянными параметрами, и единственной помехой в виде белого "Гауссовского" шума со спектральной плотностью мощности GO, полоса частот которого равна ширине спектра сигнала: FК =FС, пропускная способность (максимально возможная скорость передачи информации по каналу при заданных характеристиках сигналов и помех) рассчитывается по формуле Шеннона для непрерывного Гауссовского канала без памяти:

=FК log2 (1 + PC/ PШ), (бит/c) (10.1)
где FК - полоса частот канала, равная ширине спектра модулированного сигнала:
FК =FМОД . (10.2)
РС/ Pш - отношение сигнал /шум (мощностей сигнала и шума) на входе детектора.

Т.к. РС = Е/ТТАКТ = Е FТАКТ, а РШ = GO FК = GO FМОД и Е = h2 GO, то:

РС/ РШ = h2 FТАКТ/ FМОД . (10.3)
Для ДОФМ сигналов
FМОД = FК = FДОФМ =(23)∙FТАКТ

_{Получим} FМОД =FК = FДОФМ =2∙FТАКТ=2∙88∙103=176∙103(Гц)=176(кГц).

РС/ РШ = h2/2 = 21,64 /2=10,82

FК = FДОФМ = 176(кГц)

С = 176 103 ∙log2(1+10,82)=176 103 ∙3,563= 627,09∙103 (бит/c)=627,09(кбит/с)
При увеличении полосы частот канала FК до бесконечности, пропускная способность канала стремится к пределу, называемому потенциально возможной пропускной способностью канала (теорема Шеннона):

C = lim C = (PC/ GO) log2е, (бит/с). (10.4)

FК

Так как РС = Е FТАКТ = h2 GO FТАКТ, то C = h2 FТАКТ log2е, (бит/с).е=lge/lg2≈1,4329594 = 21,64 88 103 1,4329594 =2,73106(бит/c)=2,73(Мбит/с) /C = 2,73106/627,09∙103 = 4,35
Заключение
Потенциальная возможность пропускной способности канала по теореме Шеннона в 4,35 раза превышает пропускную способность реального канала нашей системы связи. Эффективность использования пропускной способности канала при оптимальном некогерентном приёме помехоустойчивых ДМ сигналов достаточно высока.

Опишем взаимосвязь пропускной способности канала и его полосы пропускания.

Максимальную скорость, с которой канал способен передавать данные, называют пропускной способностью канала или битовой скоростью.

Найквист открыл взаимосвязь между пропускной способности канала и шириной его полосы пропускания.

Теорема Найквиста:

= 2H∙log2M (бит/с), (10.5)

где Vmax- максимальная скорость передачи, H - ширина полосы пропускания канала, выраженная в Гц, М - количество уровней сигнал, используемых при передаче. Например, из этой формулы следует, что канал с полосой 3 кГц не может передавать двухуровневые сигналы быстрее 6000 бит/с.

Эта теорема также показывает, что, например, бессмысленно сканировать линию чаще, чем удвоенная ширина полосы пропускания. Действительно, все частоты выше этой отсутствуют в сигнале, а поэтому вся информация, необходимая для восстановления сигнала будет собрана при таком сканировании.

Однако теорема Найквиста не учитывает шум в канале, который измеряется как отношение мощности полезного сигнала к мощности шума: S/N. Эта величина измеряется в децибелах: 10∙log10(S/N)(дБ). Например, если отношение S/N равно 10, то говорят о шуме в 10 Дб, если отношение равно 100, то 20 дБ.

На случай канала с шумом есть теорема Шеннона, по которой максимальная скорость передачи данных по каналу с шумом равна:

∙log2 (1+S/N) (бит/с) (10.6), где S/N - соотношение сигнал-шум в канале

Здесь уже не важно количество уровней в сигнале. Эта формула устанавливает теоретический предел, которой редко достигается на практике. Например, по каналу с полосой пропускания в 3000 Гц и уровнем шума 30Дб (это характеристики телефонной линии) нельзя передать данные быстрее, чем со скоростью 30000 (бит/с).

Нижеследующая теорема дает прямую наглядную интерпретацию ошибочности, показывая, кроме того, что это единственная подходящая мера.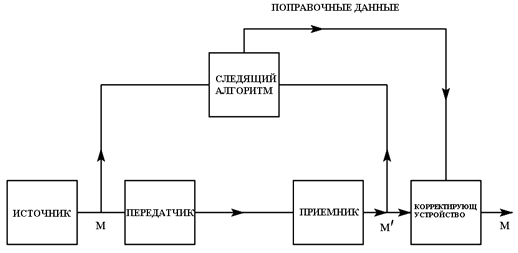


Рис. 10.1. Схематическое изображение корректирующей системы.
Теорема: Если пропускная способность корректирующего канала , можно закодировать корректирующую информацию таким образом, что ее можно послать по этому каналу и скорректировать все ошибки за исключением их произвольно малой доли . Это невозможно, если пропускная способность корректирующего канала меньше.

- количество дополнительной информации, необходимой приемнику для коррекции принятого сообщения. Для доказательства первой части рассмотрим длинные последовательности принятого сообщения и исходного сообщения . Есть логарифмически большое число сообщений M, которые могли бы привести к принятому сообщению . Таким образом, необходимо передавать двоичных цифр каждые T секунд. Это может быть сделано при частоте ошибок в канале с пропускной способностью . Второе утверждение может быть доказано, если для доказательства второго утверждения заметим, что для любых дискретных случайных величин x, y, z.