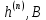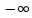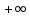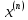1. тэс курсач. Курсовая работа по дисциплине Теория электрической связи
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
Задание 2Считая, что исходное сообщение воздействует на идеальный фильтр нижних частот (ИФНЧ) с единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения: а) Рассчитать среднюю квадратическую погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ; 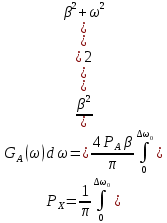 (5.2.1) (5.2.1)Средняя квадратическая погрешность фильтрации: 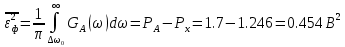 (5.2.2) (5.2.2)Найдем частоту и интервал временной дискретизации отклика ИФНЧ: 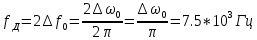 (5.2.3) (5.2.3)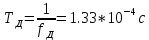 (5.2.4) (5.2.4)5.3 Задание 3Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования: а) Рассчитать интервал квантования, пороги и уровни квантования, среднюю квадратическую погрешность квантования (СКПК);  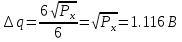 (5.3.1) (5.3.1)Пороги квантования находим из выражения: 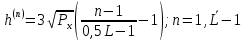 (5.3.2) (5.3.2)Результаты вычислений сводим в таблицу 5.3.1. Таблица 5.3.1 – Пороги квантования
Уровни квантования определяются следующими соотношениями: 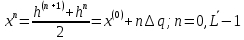 (5.3.3) (5.3.3)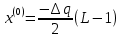 (5.3.4) (5.3.4)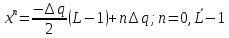 (5.3.5) (5.3.5)Результаты вычислений сводим в таблицу 5.3.2. Таблица 5.3.2 – Уровни квантования
Средняя квадратическая погрешность квантования (мощность шума квантования) равна: 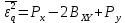 , где: (5.3.6) , где: (5.3.6)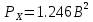 (5.3.7) (5.3.7)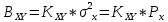 (5.3.8) (5.3.8)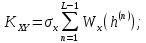 (5.3.9) (5.3.9)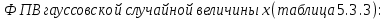 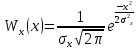 (5.3.10) (5.3.10)Таблица 5.3.3 - ФПВ гауссовской случайной величины x
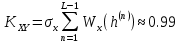 (5.3.11) (5.3.11)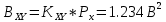 (5.3.12) (5.3.12)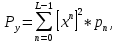 (5.3.13) (5.3.13)Где 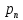 – распределение вероятностей дискретной случайной величины – распределение вероятностей дискретной случайной величины y= 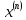 , n , n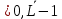 (5.3.14) (5.3.14)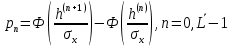 (5.3.15) (5.3.15)Где Ф(v) = 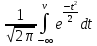 – табулированная функция Лапласа. – табулированная функция Лапласа.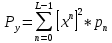 (5.3.16) (5.3.16)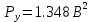 (5.3.17) (5.3.17)Следовательно, получаем, что мощность шума квантования равна: 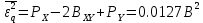 (5.3.17) (5.3.17)б) Построить в масштабе характеристику квантования (рис. 5.3.1). 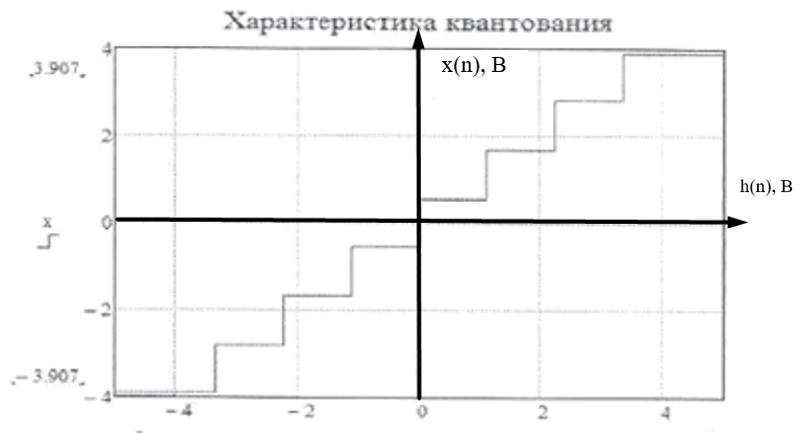 Рисунок 5.3.1 - График характеристики квантования |