1. тэс курсач. Курсовая работа по дисциплине Теория электрической связи
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
5.4 Задание 4Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L-ичного дискретного канала связи (ДКС): а) рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность L-ичного дискретного источника; Распределение вероятностей рассчитывается так: 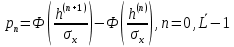 (5.4.1) (5.4.1)Где Ф(v) = 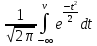 – табулированная функция Лапласа. – табулированная функция Лапласа.Распределение вероятностей приведено в таблице 5.4.1. Таблица 5.4.1 - Распределение вероятностей
Интегральное распределение вероятностей. 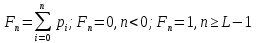 (5.4.2) (5.4.2)Информационная содержательность сообщения определяется вероятностью его появления. Количество информации, которое заключено в некотором сообщении с вероятностью появления p(i) равно: 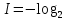 p(i) (5.4.3) p(i) (5.4.3)Основание логарифма определяет единицы измерения количества информации. В теории информации основание логарифма принимают равным 2, т. е. количество информации измеряют в двоичных единицах (1 дв. ед.) или битах (1 бит). Одна двоичная единица информации или бит – это количество информации, которое мы получаем, если произошло событие, вероятность появления которого равна 0.5. Энтропия – это среднее количество информации, приходящееся на одно сообщение, символ, слово источника информации. Для дискретного источника информации символы в кодовом слове – независимы и могут принимать одно из mвозможных значений. В этом случае энтропия дискретного источника независимых символов равна: 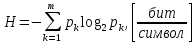 (5.4.4) (5.4.4)Рассчитаем энтропию. 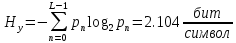 (5.4.5) (5.4.5)Производительность в ДКС определяется соотношением: 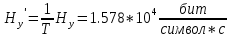 (5.4.6) (5.4.6)Избыточность последовательности источника. 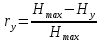 (5.4.7) (5.4.7)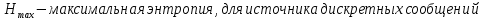 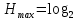 L=3 L=3 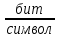 (5.4.8) (5.4.8)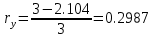 (5.4.9) (5.4.9)б) Построить в масштабе графики рассчитанных закона и функции распределения вероятностей. График закона распределения вероятностей представлен на рисунке 5.4.1. 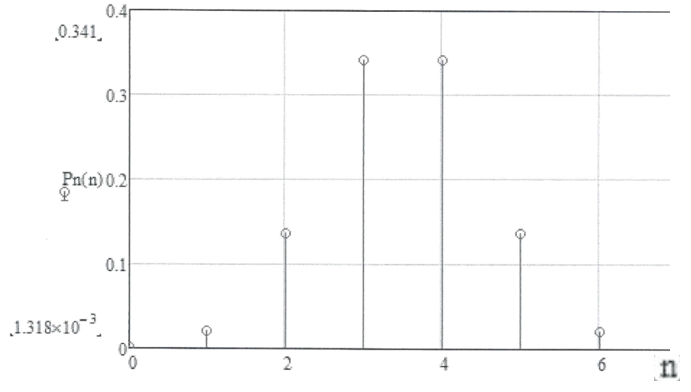 Рисунок 5.4.1 - График закона распределения вероятностей График функции распределения вероятностей представлен на рисунке 5.4.2. 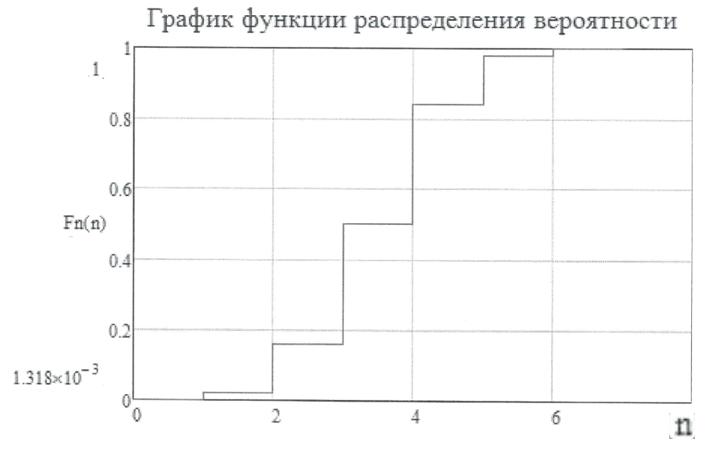 Рисунок 5.4.2 - График функции распределения вероятностей |