курсовая работа (задача) теория многофазных течений. курсовая теория многофазных течений. Курсовая работа По дисциплине Теория многофазных течений
 Скачать 144.96 Kb. Скачать 144.96 Kb.
|
3. Решение задачиНа шар, брошенный под углом к горизонту, действуют сила тяжести, силу Архимеда, силу трения и действие ветра. Тогда уравнение движение шара имеет следующий вид: 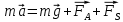 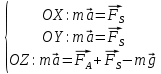 Что бы получили значения изменения скоростей движения шара и его координат, будем использовать численные методы. Методы Рунге – Кутта – это большой класс численных методов решения задачи Коши для обыкновенных дифференциальных уравнений и их систем. Первые методы данного класса были предложены около 1900 года немецкими математиками К. Рунге и М. Кутта. К классу методов Рунге – Кутта относятся явный метод Эйлера и модифицированный метод Эйлера с пересчётом, которые представляют собой соответственно методы первого и второго порядка точности. Существуют стандартные явные методы третьего порядка точности, не получившие широкого распространения. Наиболее часто используется и реализуется в различных математических пакетах (Maple, MathCAD, Maxima) классический метод Рунге – Кутта, имеющий четвёртый порядок точности. При выполнении расчётов с повышенной точностью всё чаще применяются методы пятого и шестого порядков точности. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями. Методы седьмого порядка должны иметь по меньшей мере девять стадий, а методы восьмого порядка – не менее 11 стадий. Для методов девятого и более высоких порядков (не имеющих, впрочем, большой практической значимости) неизвестно, сколько стадий необходимо для достижения соответствующего порядка точности. Среди достоинств методов Рунге – Кутта, определивших их популярность, можно выделить следующее: Эти методы легко программируются, Эти методы обладают достаточными для широкого круга задач свойствами точности и устойчивости. Эти методы (как и все одношаговые методы) являются самостартующими и позволяют на любом этапе вычислений легко изменять шаг интегрирования. Классический метод Рунге – Кутта четвёртого порядка Метод Рунге – Кутта четвёртого порядка при вычислениях с постоянным шагом интегрирования столь широко распространён, что его часто называют просто методом Рунге – Кутта. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка. Далее  ; ;  . .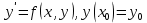 . .Тогда приближенное значение в последующих точках вычисляется по итерационной формуле: 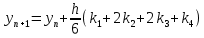 Вычисление нового значения проходит в четыре стадии: 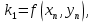 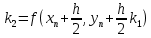 , ,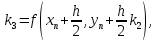 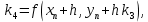 где 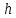 – величина шага сетки по – величина шага сетки по 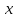 . .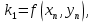 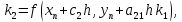 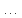 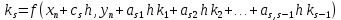 Конкретный метод определяется числом 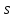 и коэффициентами и коэффициентами 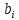 , , 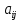 и и 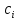 . Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Батчера). . Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Батчера).Этот метод имеет четвёртый порядок точности. Это значит, что ошибка на одном шаге имеет порядок O ( 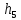 ), а суммарная ошибка на конечном интервале интегрирования имеет порядок O ( ), а суммарная ошибка на конечном интервале интегрирования имеет порядок O (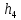 ). ). Явные методы Рунге – Кутта Семейство явных методов Рунге – Кутта является обобщением как явного метода Эйлера, так и классического метода Рунге – Кутта четвёртого порядка. Оно задаётся формулами: 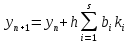 где 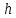 – величина шага сетки по – величина шага сетки по 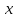 и вычисление нового значения проходит в и вычисление нового значения проходит в 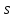 этапов. этапов.Явные методы Рунге – Кутта, как правило, непригодны для решения жестких уравнений из-за малой области их абсолютной устойчивости. Неустойчивость явных методов Рунге – Кутта создаёт весьма серьёзные проблемы и при численном решении дифференциальных уравнений в частных производных. Неустойчивость явных методов Рунге – Кутта мотивировала развитие неявных методов. Неявный метод Рунге – Кутта имеет вид: 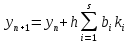 где 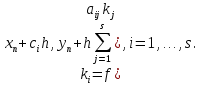 Явный метод характерен тем, что матрица коэффициентов 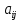 для него имеет нижний треугольный вид (включая и нулевую главную диагональ) в отличие от неявного метода, где матрица имеет произвольный вид. для него имеет нижний треугольный вид (включая и нулевую главную диагональ) в отличие от неявного метода, где матрица имеет произвольный вид. Преимуществом неявных методов Рунге – Кутта в сравнении с явными является их большая устойчивость, что особенно важно при решении жестких уравнений. Простейшим неявным методом Рунге – Кутта является модифицированный метод Эйлера «с пересчётом». Решение систем дифференциальных уравнений методом Рунге – Кутта является одним из самых распространённых численных методов решений в технике. Рассмотрим силы, действующие относительно оси ОХ: 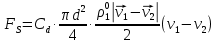 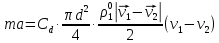 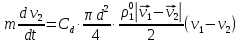 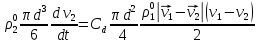 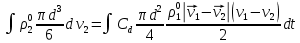 Тогда уравнение скорости движения шара относительно оси ОХ имеет следующий вид: 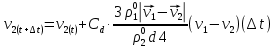 Рассмотрим силы, действующие относительно оси OY: 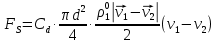 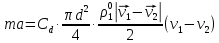 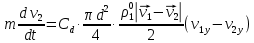 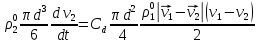 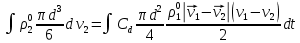 Тогда уравнение скорости движения шара относительно оси ОY имеет следующий вид: 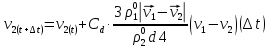 Рассмотрим силы, действующие относительно оси OZ: 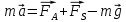 Принимая во внимание, что: 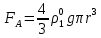 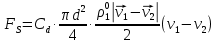 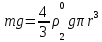 Получаем следующий вид уравнения движения относительно оси ОZ: 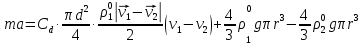 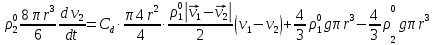 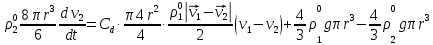 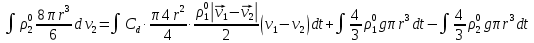 Уравнение скорости движения шара относительно оси ОZ имеет следующий вид: 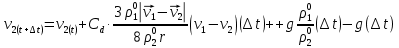 Координаты точек нахождения шара в определенные моменты времени рассчитываем по следующим формулам: 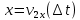 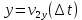 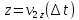 Для нахождения модуля вектора скорости (длины вектора) по известным координатам скоростей используем следующую формулу: 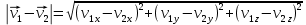 Значение скорости рассчитываем исходя из значений скоростей по каждой из оси по формуле: 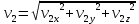 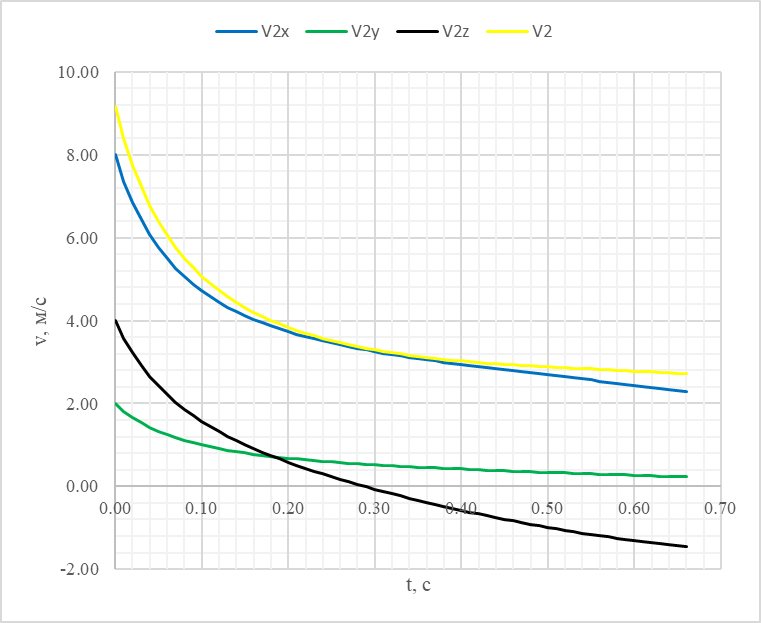 Рисунок 1. – Изменение скорости шара 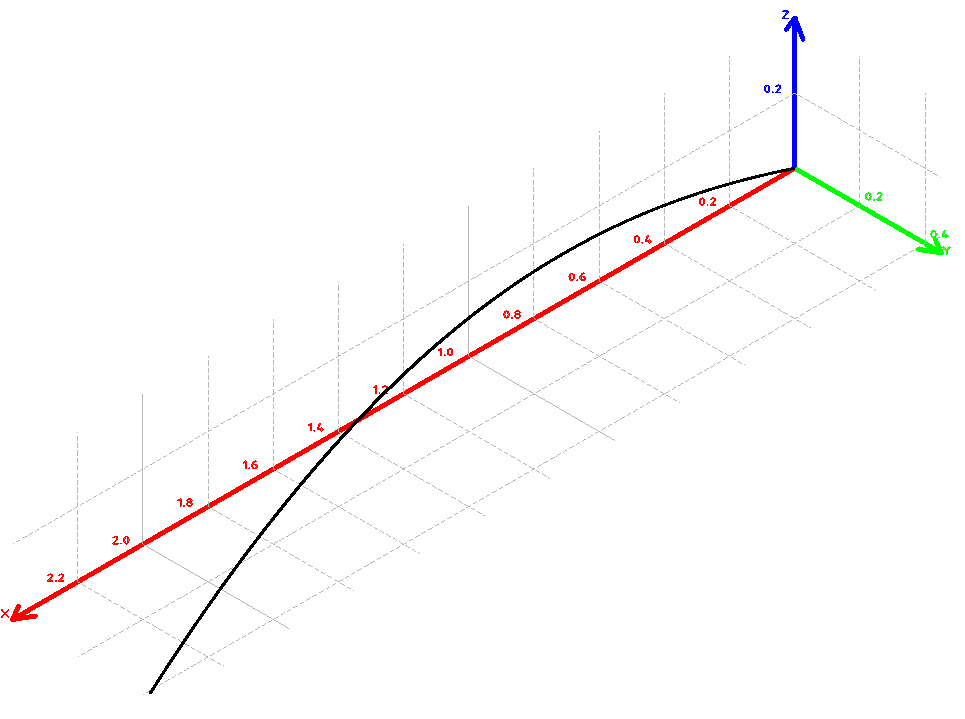 Рисунок 2. – траектория движения шара |
