отчет по Методу Монте-Карло Тимофеев Владимир РТ-21 — копия. Отчет Метод МонтеКарло Тимофеев Владимир Группа Рт21 Проверила Тимофеев Т. Е г. Якутск 2022
 Скачать 473.94 Kb. Скачать 473.94 Kb.
|
|
Министерство образования Российской Федерации Северо-Восточный федеральный университет им М.К.Аммосова Кафедра радиофизики и радиотехники Отчет Метод Монте-Карло Выполнил: Тимофеев Владимир Группа: Рт-21 Проверила: Тимофеев Т.Е г.Якутск 2022 Содержание Введение История Метода Монте-Карло Теоретическая часть Способ интегрирования Монте-Карло Практическая часть Линейный способ Способ Монте-Карло Вывод Введение Методами Монте-Карло называют численные методы решения математических задач при помощи моделирования случайных величин. Однако , решать методами Монте-Карло можно любые математические задачи, а не только задачи вероятностного происхождения, связанные со случайными величинами .Важнейшим приемом построения методов Монте-Карло является сведение задачи к расчету математических ожиданий. Так как математические ожидания чаще всего представляют собой обычные интегралы, то центральное положение в теории метода Монте-Карло занимают методы вычисления интегралов .Преимущества недетерминированных методов особенно ярко проявляются при решении задач большой размерности, когда применение традиционных детерминированных методов затруднено или совсем невозможно .Границы между простым и сложным, возможным и невозможным существуют всегда, но с развитием вычислительной техники сдвигаются вдаль .До появления электронных вычислительных машин (ЭВМ) методы Монте-Карло не могли стать универсальными численными методами, ибо моделирование случайных величин вручную весьма трудоемкий процесс. Развитию методов Монте-Карло способствовало бурное развитие ЭВМ. Алгоритмы Монте-Карло сравнительно легко программируются и позволяют производить расчеты во многих задачах, недоступных для классических численных методов. Так как совершенствование ЭВМ продолжается , есть все основания ожидать дальнейшего развития методов Монте-Карло и дальнейшего расширения области их применения. История метода Монте-Карло Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений . Определение метода можно сделать более общим, говоря не о случайных величинах, а о случайных функциях . Идея моделирования случайных явлений известна давно и, по мнению некоторых авторов, восходит ко временам Древнего Вавилона и Ветхого Завета. Что же касается использования такого рода явлений для целей приближенных вычислений, то первой работой в этой области принято считать работу Холла 1873 г. о вычислении числас помощью случайных бросаний иглы на разграфленную параллельными линиями бумагу . Существуют также ряд более поздних работ, в которых до появления электронных вычислительных машин (ЭВМ) использовались по существу идеи метода Монте-Карло. Однако, до появления ЭВМ этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины вручную – очень трудоемкий процесс. Поэтому, идеи эти не получили заметного развития вплоть до 1944 г., когда в связи с работами по созданию атомной бомбы Дж. фон Нейман предложил широко использовать аппарат теории вероятностей для решения прикладных задач с помощью ЭВМ. Первая работа, где этот вопрос систематически излагался, принадлежит Метрополису и Уламу. В Советском Союзе первые статьи о методе Монте-Карло были опубликованы в 1955-1956 годах . В настоящее время имеется более двух тысяч работ, где исследуются теоретические основы метода или рассматриваются его применения к конкретным задачам. Метод используется для решения прикладных задач из большого числа областей науки и техники . Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались малопригодными. Далее его влияние распространилось на широкий круг задач статистической физики, очень разных по своему содержанию. Монте-Карло, следует отнести задачи теории массового обслуживания, за-дачи теории игр и математической экономики, задачи теории передачи со-общений при наличии помех и ряд других .Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики (например, развитие методов численного интегрирования) и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Теоретическая часть Сущность метода Монте – Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину Х, математическое ожидание которой равно а, т. е. М(Х)= а [1]. Практически же поступают следующим образом: производят n испытаний, в результате которых получают n возможных значений величины Х; вычисляют их среднее арифметическое 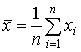 и принимают Поскольку метод Монте – Карло требует произведения большого числа испытаний, его часто называют методом статистических испытаний. Оценка погрешности метода Монте-Карло Как отмечалось, для получения оценки математического ожидания случайной величины Х необходимо произвести n независимых испытаний и по ним найти выборочную среднюю, которая принимается в качестве искомой оценки. При каждой конечной серии испытаний будут получаться различные значения случайной величины и, следовательно, другая средняя, а значит, и другая оценка математического ожидания. Очевидно, что получить точную оценку математического ожидания невозможно. Поэтому возникает вопрос о допускаемой ошибке. Обычно ограничиваются отысканием лишь верхней границы δдопускаемой ошибки с заданной вероятностью γ, т. е. При этом возможны следующие случаи оценки числа испытаний: 1. Случайная величина Х распределена нормально и ее среднее квадратическое отклонение (стандартное отклонение) σ известно. В этом случае с заданной вероятностью γ верхняя граница ошибки определяется по формуле 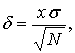 (4.1) (4.1)где N – число испытаний (разыгранных значений случайной величины Х); х – значение аргумента функции Лапласа Ф(х) или интеграла вероятности, при котором она равно половине заданной вероятности, σ – известное среднее квадратическое отклонение. Из формулы (2.1) может быть найдено число испытаний. Один из вариантов интеграла вероятностей (функции Лапласа) имеет вид [1]: Способ интегрирования Метода Монте-Карло Когда говорят о интегрировании методом Монте-Карло, обычно подразумевают метод, при котором область интегрирования [a, b] делится случайным образом на участки шириной (a — b)/N, где N — количество случайных точек, и затем площадь получившихся столбиков суммируется. Формула для вычисления интеграла этим методом выглядит так: 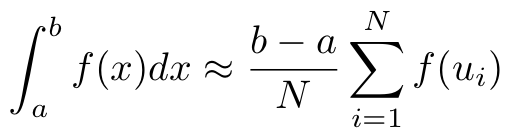 Однако есть еще иной геометрический метод Монте-Карло, удивительный по своей простоте и эффективности. Для этого метода нужно взять область интегрирования [a, b], ограничить ее прямоугольником с площадью Spar и набросать в этот прямоугольник случайным образом точек. Затем требуется посчитать количество точек K попавших в область под графиком функции и вычислить интеграл (площадь под кривой S) по формуле: 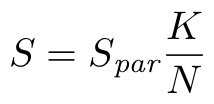 Для примера попробую посчитать этим методом интеграл функции f(x) = sin(x) / 2 на отрезке [0, 2]. При этом значение интеграла должно получиться приблизительно равным 0.708074. Ограничиваю область интегрирования прямоугольником размером 2 x 1.5: 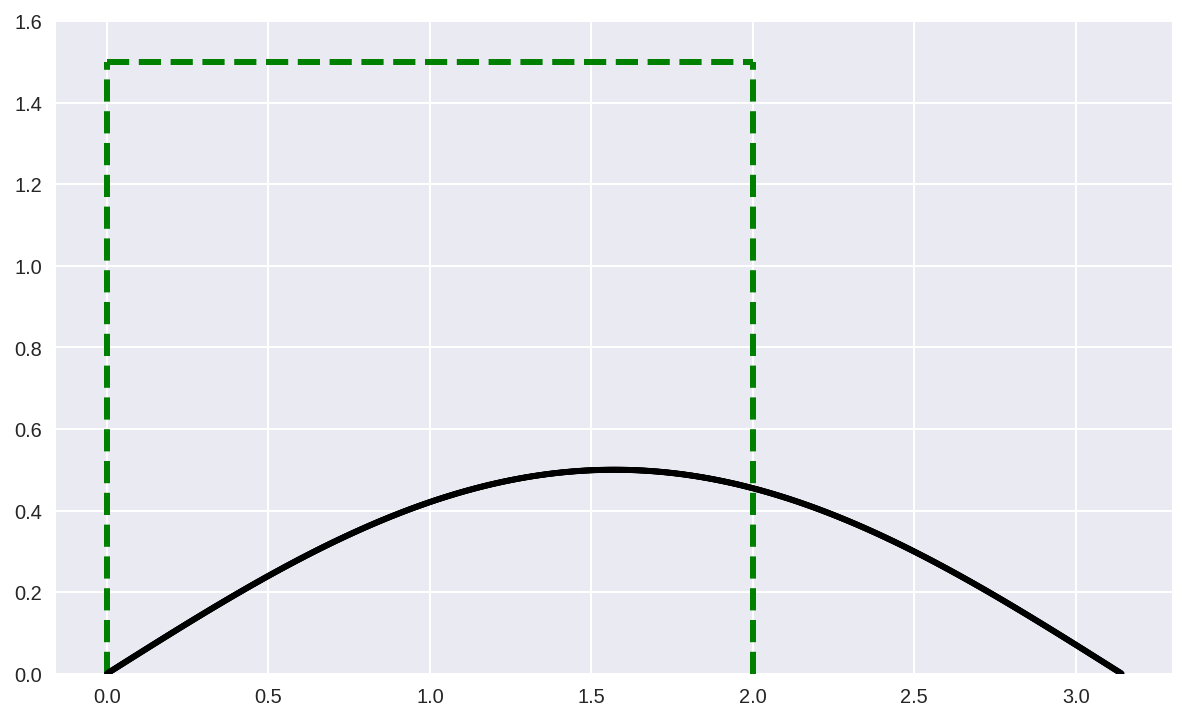 и вбрасываю сотню точек со случайными координатами . Повторяю этот эксперимент 20 раз. На изображении здесь и ниже показан один из 20 результатов: 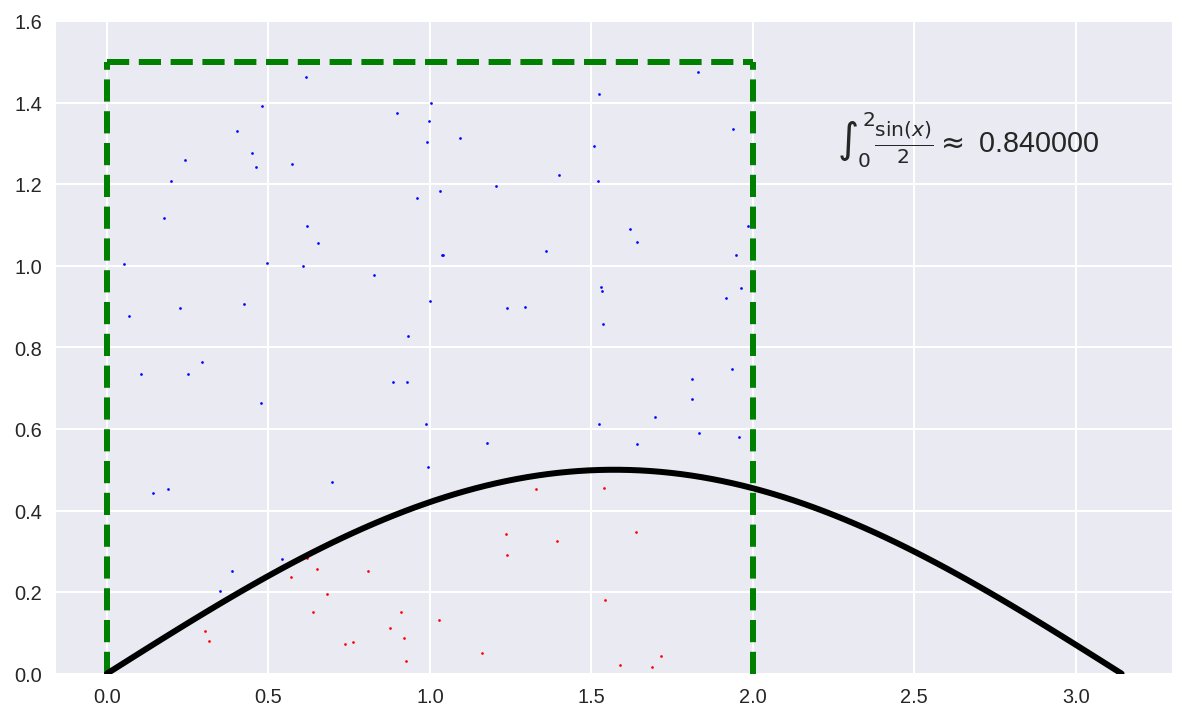 При таком малом количестве точек значение предсказуемо бессовестно скачет от 0.51 до 0.99, со средним 0.735 и такой же медианой. Увеличиваю количество точек в сто раз до 10000: 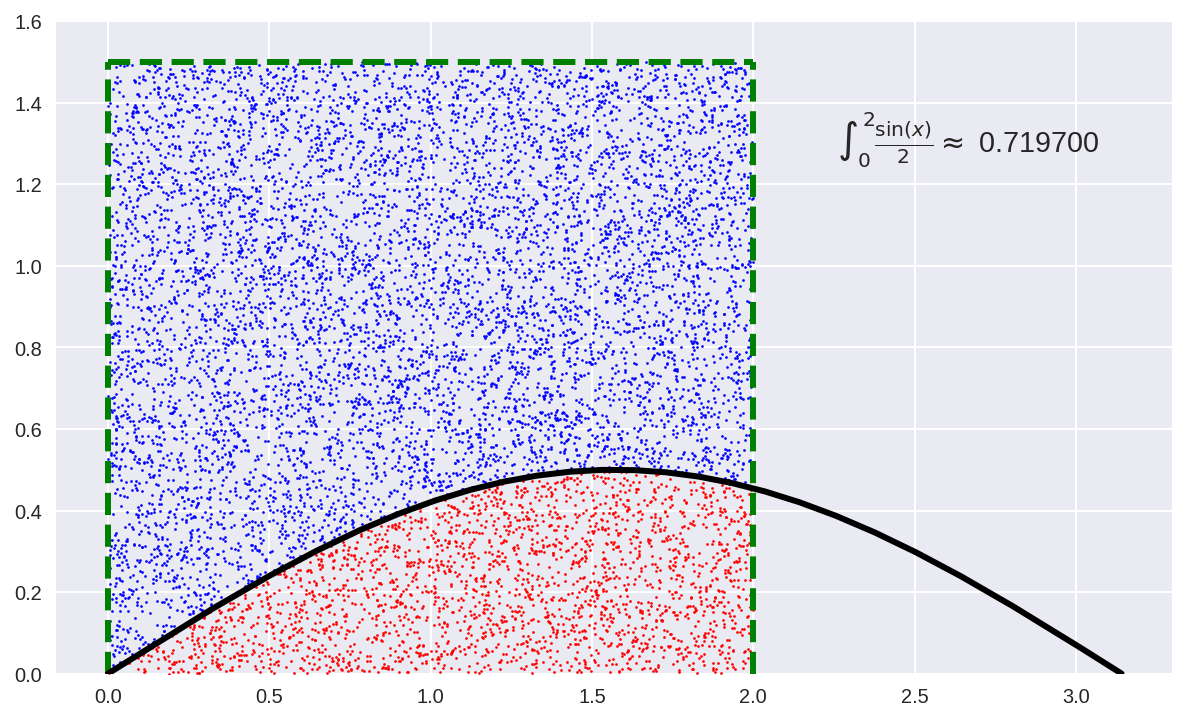 Разброс значений теперь становится значительно меньше: между 0.6849 и 0.732, со средним 0.705825 и медианой 0.7077. Увеличиваю количество точек еще сто раз 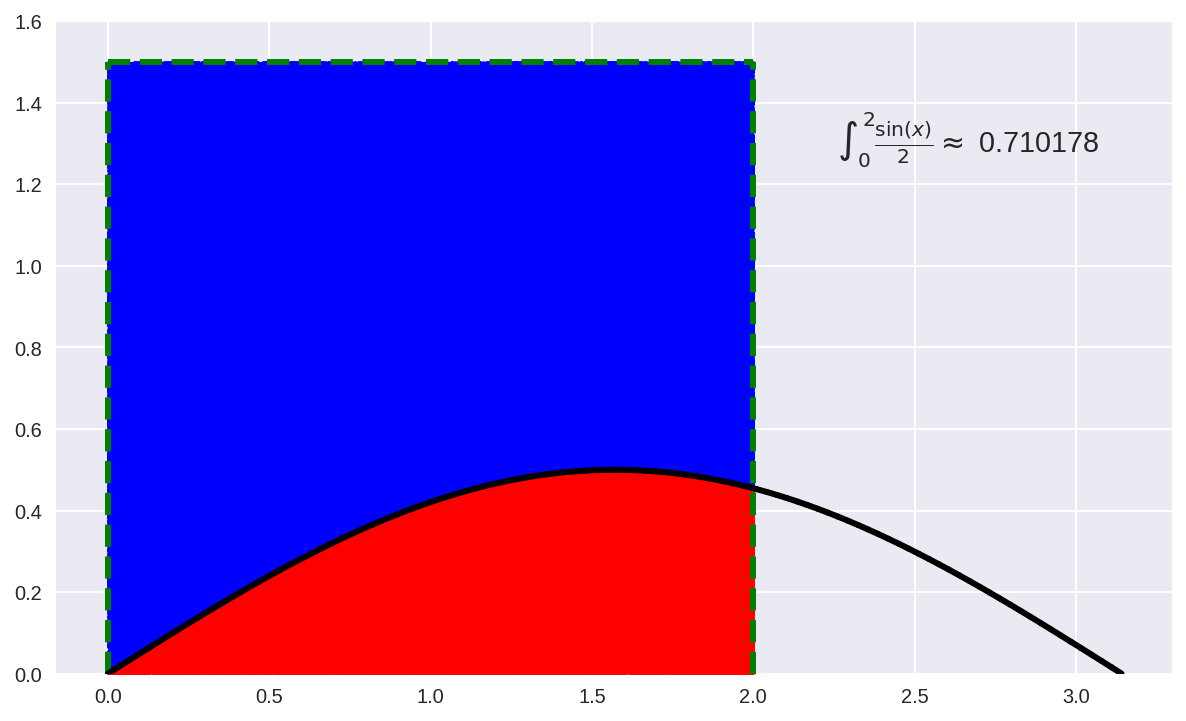 Миллион точек на изображении превращается в сплошную заливку прямоугольника. Разброс значений оказывается между 0.705135 и 0.709499, со средним 0.70764705 и медианой 0.7075275. Последняя череда экспериментов со ста миллионами точек: 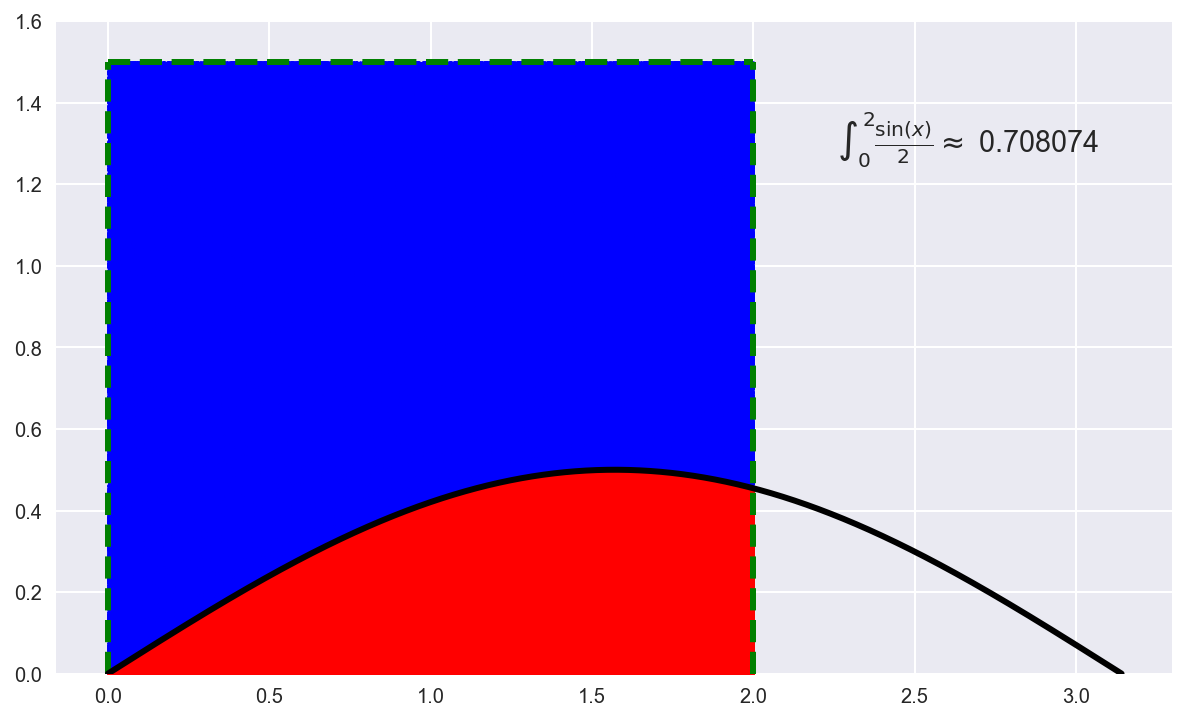 Практическая часть линейный способ. Задача Рассчитать норму амортизационных отчислений на приобретение нового оборудования, балансовая стоимость которого составляет Сб. Ликвидационная стоимость прогнозируется на уровне N% балансовой стоимости, а нормативный срок эксплуатации – Т лет. Начисление амортизации выполнить линейным методом и способом списания стоимости по сумме чисел лет.
Решение Ликвидационная стоимость оборудования составляет: Стоимость основных фондов, подлежащая амортизации равна: Сб-Сл = 4500-225 = 4275 тыс. ус. ден. ед. Начисление амортизационных отчислений линейным методом: 100/Т = 100/7 = 14,29%, или 4275/Т = 610,71 тыс. ус. ден.ед. Начисление амортизационных отчислений способом списания стоимости по сумме чисел лет: Сумма чисел лет: 1+2+3+4+5+6+7 = 28, или 7 Расчетный коэффициент для каждого года: 1-й год: 7/28 5-й год: 3/28 2-й год: 6/28 6-й год: 2/28 3-й год: 5/28 7-й год: 1/28 4-й год: 4/28 Соответственно начисленная амортизация: 1-й год: 2-й год: 3-й год: 4-й год: 5-й год: 6-й год: 7-й год: Изменение стоимости основных фондов по годам: Линейный способ:
Способ по сумме чисел лет:
Практическая часть способ Монте-Карло. Далее перейдем к методу Монте-Карло Прописываем данный код в SAGE и подставляем ту же уравнения 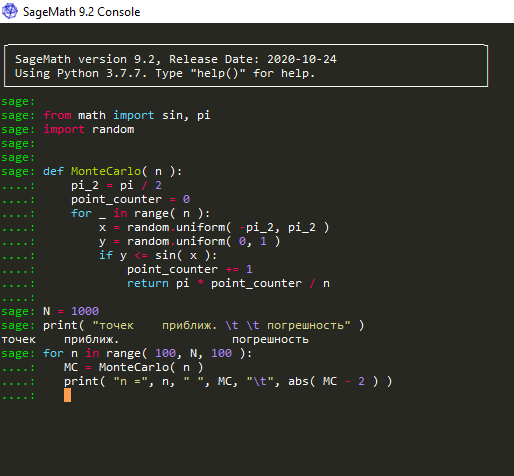 После этого программа должна выдаст ответ в виде: 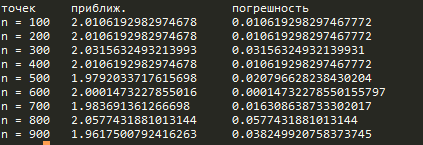 Где «точек» это случайно выбранный координат в диапазоне уравнения, где «приближ.» это ответ примерно равный к 2, где «погрешность» это погрешность ответа (возникает из-за случайного выбора координата). Вывод: В ходе решения я научился решать задачи двумя способами (Линейный способ и метод Монте-Карло) , с которыми я буду использовать и в дальнейшем, так как методы оптимизируют скорость решения задачи. Решая двумя методами получил один и тот же ответ, это означает правильность решения методов. |
