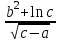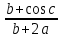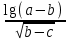лекция. Лекция 2. Лекция 2 Способы приближенных вычислений по заданной формуле
 Скачать 98.46 Kb.
|
|
Лекция 2 «Способы приближенных вычислений по заданной формуле» План лекции Способы приближенных вычислений по заданной формуле. Вычисление по правилам подсчета цифр. Вычисление со строгим учётом предельных абсолютных погрешностей. Вычисление по методу границ. Наиболее распространенный вид вычислений – это вычисления по готовой формуле. В компьютере вычисление при любой громоздкости формулы обеспечивается, как правило, одной командой. Если при этом программно не предусматривается контроль вычислительных погрешностей, вычислитель анализирует результат в конце счета. Иногда условия вычислительной задачи заставляют вести пооперационный учет движения вычислительной погрешности. При этом сохраняется возможность получить достоверный окончательный результат методом его итогового округления. Рассмотрим приемы вычислений, учитывающие как пооперационную, так и итоговую методику оценки точности. Вычисление по правилам подсчета цифр При вычислении данным методом явного учёта погрешностей не ведётся, Правила подсчёта цифр показывают лишь, какое количество значащих цифр или десятичных знаков в результате можно считать надёжными. Правила метода: При сложении и вычитании приближенных чисел следует считать верными столько десятичных знаков после запятой, сколько их в приближенном данном с наименьшим числом знаков после запятой. При умножении и делении приближенных чисел нужно выбрать число с наименьшим количеством значащих цифр и округлить остальные числа так, чтобы в них было лишь на одну значащую цифру больше, чем в наименее точном числе. При определении количества верных цифр в значениях функций от приближённых значений аргумента следует грубо оценить значение модуля производной функции. Если это значение не превосходит единицы или близко к ней, то в значении функции можно считать верными столько знаков после запятой, сколько их имеет значение аргумента. Если же модуль производной функции превосходит единицу, то количество верных десятичных знаков в значении функции меньше, чем в аргументе на величину, равную разряду оценки производной. В записи промежуточных результатов следует сохранять на одну цифру больше, чем описано в правилах 1-3. В окончательном результате эта запасная цифра округляется. Правила подсчёта цифр носят оценочный характер, но практическая надёжность этих правил достаточно высока. При исследовании данного метода используется расчётная таблица – расписка формул. Пример: Вычислить значение функции 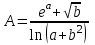 , а = 2,156, b = 0,927.Решение: Пошаговые вычисления для удобства будем проводить в таблице, в правом столбце, которой записываем пояснения. Таблица 2.1
Вычисление со строгим учётом предельных абсолютных погрешностей Этот метод предусматривает использование правил вычисления предельных абсолютных погрешностей. При пооперационном учете ошибок промежуточные результаты, так же как и их погрешности, заносятся в специальную таблицу, состоящую из двух параллельно заполняемых частей – для результатов и их погрешностей. В таблице приведены пошаговые вычисления со строгим учетом предельных абсолютных погрешностей по той же формуле, что и в предыдущем примере, и в предположении, что исходные данные a и b имеют предельные абсолютные погрешности 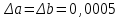 (по формуле 1.3), т.е. у a и b все цифры верны.Промежуточные результаты вносятся в таблицу после округления до одной запасной цифры; значения погрешностей для удобства округляются (с возрастанием!) до двух значащих цифр. Проследим ход вычислений на одном этапе. Пример: Вычислить значение функции 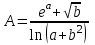, а = 2,156, b = 0,927.Решение: Все вычисления также проведем в таблице. Вычисляем значение функции в заданной точке и погрешность результата. Таблица 2.2
Используя калькулятор, имеем 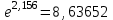 . При вычислении предельных абсолютных погрешностей используем таблицу 1.2. 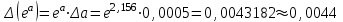 .Судя по ее величине, в полученном значении экспоненты в строгом смысле верны два знака после запятой. Округляем это значение с одной запасной цифрой: 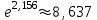 и вносим его в таблицу. При этом возникает погрешность округления: 8,637-8,63652=0,00048. Вслед за этим вычисляем полную погрешность полученного результата (погрешность действия плюс погрешность округления: 0,0044+0,00048=0,0049), которую так же вносим в таблицу. Все последующие действия выполняем аналогично с применением соответствующих формул для предельных абсолютных погрешностей. Округляя окончательный результат до последней верной в строгом смысле цифры, а так же округляя погрешность до соответствующих разрядов результата, окончательно получаем: А = 8,7 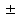 0,1. Вычисления по методу строго учёта предельных абсолютных погрешностей можно выполнить на компьютере с помощью программы. Если не производить пооперационного учёта движения вычислительной ошибки, то достаточно вычислить значение предельной абсолютной погрешности окончательного результата, а затем произвести его округление. Вычисление по методу границ Если нужно иметь абсолютно гарантированные границы возможных значений вычисляемой величины, используют специальный метод вычислений – метод границ. Пусть f(x, y) – функция непрерывная и монотонная в некоторой области допустимых значений аргументов x и y. Нужно получить её значение f(a, b), где a и b – приближенные значения аргументов, причем достоверно известно, что 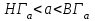 ;  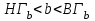.Здесь НГ, ВГ - обозначение соответственно нижней и верхней границ значений параметров. Итак, вопрос состоит в том, чтобы найти строгие границы значения f(a, b) при известных границах значений a и b. Допустим, что функция f(x, y) возрастает по каждому из аргументов x и y. Тогда 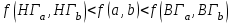 .Пусть теперь f(x, y) возрастает по аргументу x и убывает по аргументу y. Тогда будет строго гарантировано неравенство 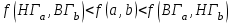 .Рассмотрим указанный принцип на примере основных арифметических действий. Пусть 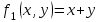 . 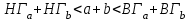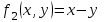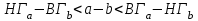Тогда очевидно, что .Точно так же для функции  (она по x возрастает, а по y убывает) имеем .Аналогично для умножения и деления: 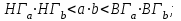 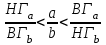 Рассмотрим функцию 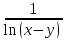 . Замечаем, что при увеличении x она убывает, а с увеличением y – возрастает. Следовательно, имеет место неравенство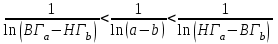 .Вычисляя по методу границ с пошаговой регистрацией промежуточных результатов, удобно использовать обычную вычислительную таблицу, состоящую из двух строк – отдельно для вычисления НГ и ВГ результата (по этой причине метод границ называют ещё методом двоичных вычислений). При выполнении промежуточных вычислений и округлении результатов используются все рекомендации правил подсчёта цифр с одним важным дополнением: округление нижних границ ведётся по недостатку, а верхних - по избытку. Окончательные результаты округляются по этому же правилу до последней верной цифры. Пример: Вычислить значение функции 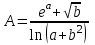, а = 2,156, b = 0,927.Решение: Нижняя и верхняя границы значений a и b определены из условия, что в исходных данных: а = 2,156 и b = 0, 927, все цифры верны ( 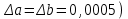 , т.е. 2,1555 < a < 2,1565; 0,9265 < b < 0,9275. Таблица 2.3
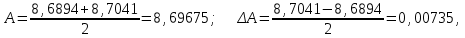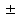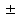Таким образом, результат вычислений значения А по методу границ имеет вид 8,6894 < А < 8,7041. По результатам вычислений получаем  что дает А = 8,697 0,008, или при записи верными цифрами, А=8,7 0,01.Контрольные вопросы Как формулируются правила подсчета цифр? Какова последовательность действий на каждом промежуточном этапе расчетной таблицы в вычислениях по правилам подсчета цифр с пооперационным учетом ошибок? на заключительном этапе? Как оформляются вычисления со строгим учетом предельных погрешностей при пооперационном учете ошибок? Какова последовательность действий на каждом промежуточном этапе расчетной таблицы в вычислениях по методу строгого учета предельных погрешностей с пооперационным учетом ошибок? на заключительном этапе? Как вычисляются предельные погрешности результата при использовании методики итоговой оценки ошибки вычислений? В чем основное отличие метода границ от вычислений по методу строгого учета границ погрешностей? Какова последовательность действий на каждом промежуточном этапе расчетной таблицы в вычислениях по методу границ с пооперационным учетом ошибок? на заключительном этапе? Задачи Вычислите с помощью МК значение величины Z при заданны значениях параметров a, b иc, использую «ручные» расчетные таблицы для пошаговой регистрации результатов вычислений, тремя способами: по правилам подсчета цифр; с систематическим учетом границ абсолютных погрешностей; по способу границ. Сравните полученные результаты между собой, прокомментируйте различие методов вычислений и смысл полученных числовых значений.
Практические занятия Практическое занятие №1 «Использование основных численных методов решения математических задач. Вычисление погрешностей результатов арифметических действий» |
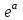
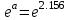= 8,63652, 
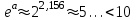, значит (используя правило 3), надо сохранить на один знак меньше, чем в значении аргумента + 1 запасная цифра.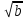
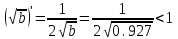, (используя правило 3) сохраняем три цифры как в аргументе + 1 запасная цифра.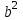
,
,
,
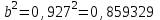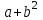
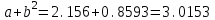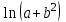
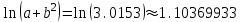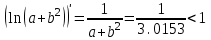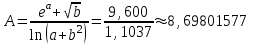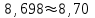
, (используя правило 3) сохраняем три цифры как в аргументе + 1 запасная цифра.
,
а
