Курсовая работа по дисциплине Теория подвижного состава
 Скачать 1.72 Mb. Скачать 1.72 Mb.
|
|
Разгон подвижного состава Основными показателями подвижного состава при разгоне являются величина ускорения, время и путь, который проходит подвижной состав за время разгона. Ускорение при разгоне определяется для случая движения подвижного состава по горизонтальному участку дороги или рельсовому пути. Расчет ведется с использованием динамической характеристики подвижного состава, которая построена ранее: 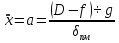 ; ;где 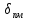 - коэффициент приведенной массы, - коэффициент приведенной массы, 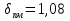 . .Так же следует иметь в виду, что ускорение подвижного состава ограниченно с целью обеспечения комфорта пассажиров и не должно превышать 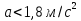 . . Проводим расчет по формуле выше. Результаты расчета сводим в таблицу (приложение Д). По результатам расчета строим график зависимости 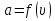 . .Из расчета видно, что максимальное ускорение 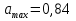 , не превышает допустимого значения. При достижении подвижным составом максимальной скорости , не превышает допустимого значения. При достижении подвижным составом максимальной скорости 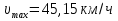 ускорение равняется нулю и разгон подвижного состава полностью прекращается. ускорение равняется нулю и разгон подвижного состава полностью прекращается.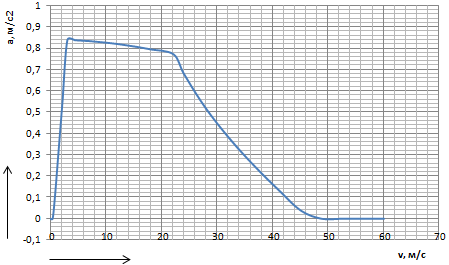 Рисунок 8 – Зависимость ускорения однозвенного троллейбуса на 90 пассажиров от его скорости Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 Определяем время разгона подвижного состава по формулам ниже. При этом полагаем, что ускорение на каждом интервале изменения скорости постоянно. Тогда время разгона на 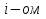 интервале будет равно: интервале будет равно: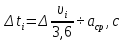 ; ;где 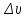 - изменение скорости на - изменение скорости на 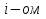 интервале, интервале, 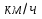 ; ;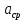 - среднее значение ускорения на - среднее значение ускорения на 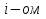 интервале, интервале, 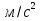 . .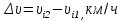 ; ;где 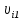 и и 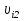 - скорости в начале и конце интервала, - скорости в начале и конце интервала, 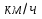 . .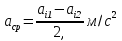 ; ;где 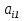 и и 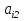 - ускорения в начале и конце интервала, - ускорения в начале и конце интервала, 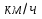 . .Отсюда, общее время разгона от 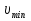 до до 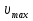 равно сумме составляющих равно сумме составляющих 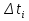 : :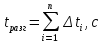 ; ;где 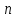 - количество интервалов изменения скорости. - количество интервалов изменения скорости. По формулам проводим расчет времени разгона. Результаты расчета сводим в таблицу (приложение Е). По полученным данным строим график зависимости 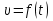 (рисунок 9). (рисунок 9).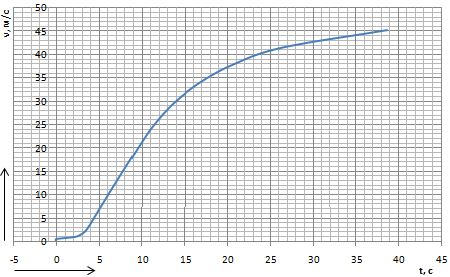 Рисунок 9 –Зависимость скорости троллейбуса от времени Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 Для получения характеристики разгона 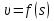 определяют приращение пути определяют приращение пути 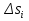 , проходимого подвижным составом на всех интервалах изменения скорости по формулам [1, с. 213].. При этом принимается допущение, что в каждом из этих интервалов подвижной состав движется с постоянной средней скоростью , проходимого подвижным составом на всех интервалах изменения скорости по формулам [1, с. 213].. При этом принимается допущение, что в каждом из этих интервалов подвижной состав движется с постоянной средней скоростью 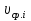 , которую определяют по формуле: , которую определяют по формуле: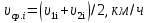 где 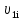 и и 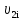 - скорости соответственно в начале и конце каждого интервала, км/ч. - скорости соответственно в начале и конце каждого интервала, км/ч.Тогда длина пути на каждом интервале: 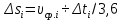 ; ;Полный путь подвижного состава за время разгона составит: 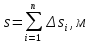 ; ;где 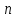 - число интервалов изменения скорости. - число интервалов изменения скорости.Графическая зависимость изменения скорости движения троллейбуса в зависимости от пути, проходимого при разгоне, представлена на рисунке 10.Результаты расчета сводим в таблицу (приложение Е). 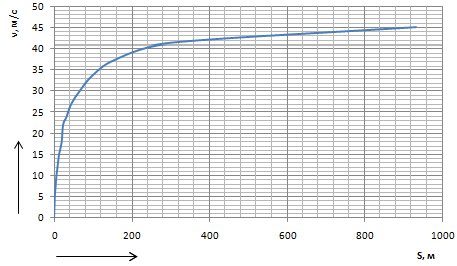 Рисунок 10 – Зависимость скорости троллейбуса от пройденного им пути Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 Индивидуальное задание Исследование колебаний пролёта ветви с двумя опорами 4.1 Общие сведения При рассмотрении колебаний упругих тел будем полагать, что материал тела однороден, изотропен и следует закону Гука. Дифференциальные уравнения движения, установленные в предыдущей главе для системы частиц, будем применять также и здесь. Однако в случае упругих тел вместо нескольких сосредоточенных масс мы имеем систему, состоящую из бесконечно большого числа частиц, между которыми действуют силы упругости. Для определения положения такой системы требуется бесконечно большое число координат, и поэтому она имеет бесконечно большое число степеней свободы, так как за возможное или виртуальное перемещение можно принять любое малое перемещение, удовлетворяющее условию непрерывности, то есть не вызывающее разрывов в теле. Поэтому любое упругое тело имеет бесконечно большое число форм собственных колебаний. В случае тонких стержней и пластинок задача колебаний может быть значительно упрощена. Эти задачи, которые имеют большое значение в технических приложениях. Одна из таких задач рассматривается в этой главе. Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 4.2 Расчётная часть Если на колеблющийся стержень действует растягивающая сила S(рисунок 1), дифференциальное уравнение для кривой прогибов при действии статической нагрузки имеет вид: 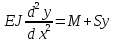 (1) (1)где 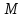 – изгибающий момент, создаваемый поперечной распределенной нагрузкойс интенсивностью – изгибающий момент, создаваемый поперечной распределенной нагрузкойс интенсивностью 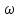 . .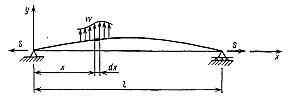 Рисунок 1 – Схема действия растягивающей силы на колеблющийся стержень Дважды продифференцировавлевую и правую части уравнения (1) по 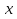 , получим: , получим: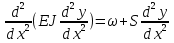 (2) (2) Для того, чтобы получить уравнение для поперечных колебаний, подставим вместо 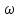 величину силы инерции, отнесенной к единице длины: величину силы инерции, отнесенной к единице длины: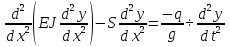 (3) (3)В случае призматического стержня постоянного сечения имеем: 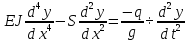 (4) (4)Предполагая, что стержень колеблется по одной из собственных форм, найдём решение уравнения (4) в следующей форме: 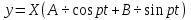 (5) (5)Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 где 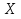 – нормальная функция – нормальная функцияПодставляя в уравнение (4) представление (5), получим: 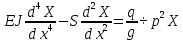 (6) (6)Решение этого уравнения, удовлетворяющее заданным концевым условиям, должно включать в себя соответствующие нормальные функции. Простейший случай имеет место при свободномопирании стержня. Эти условия будут удовлетворены, если принять следующее: 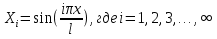 (7) (7)Продифференцируем уравнение (6)для дальнейшей подстановки и получим следующие выражения: 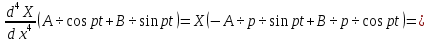 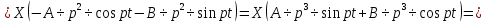 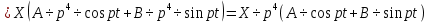 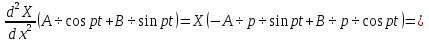 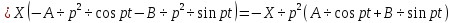 Подставляя все полученные выражения в уравнение (6), получим: 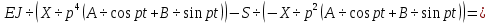 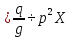 После сокращения, получим: 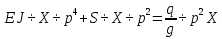 Подставляя выражение (7) в уравнение выше, получим: 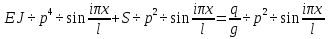 (8) (8)Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 Из уравнения (8) находим соответствующую круговую частоту колебаний, которая равна: 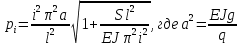 Если имеется очень податливый на изгиб стержень (допустим трос), второе слагаемое, стоящее под корнем в выражении выше, становится намного больше единицы, и если при этом 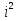 не слишком велико, можно принять: не слишком велико, можно принять: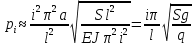 (9) (9)Выражение (9)представляет собой уравнение для собственных частот предварительно растянутой нити. Подставляя функции (7)в представление (5)для решения, найдём собственную форму колебаний, представляющую синусоиду с числом полуволн, равным 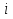 . Суммируя подобные формы, получим общее решение задачи о свободных колебаниях свободно опертого стержня при действии осевой растягивающей силы: . Суммируя подобные формы, получим общее решение задачи о свободных колебаниях свободно опертого стержня при действии осевой растягивающей силы: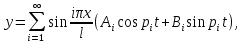 где 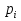 – круговая частота колебаний; – круговая частота колебаний;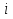 – число полуволн; – число полуволн;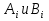 – произвольные постоянные, входящие в решение уравнения выше. – произвольные постоянные, входящие в решение уравнения выше.Таблица 1 – Параметры колебаний пролёта ветви с двумя опорами
Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 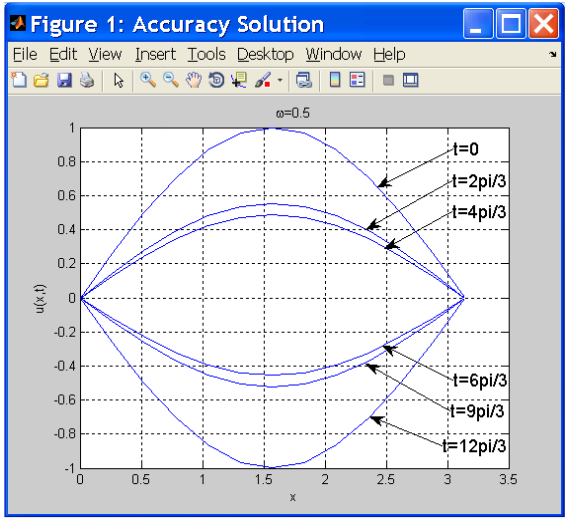 Рисунок 2 – Вынужденные колебания пролёта ветви 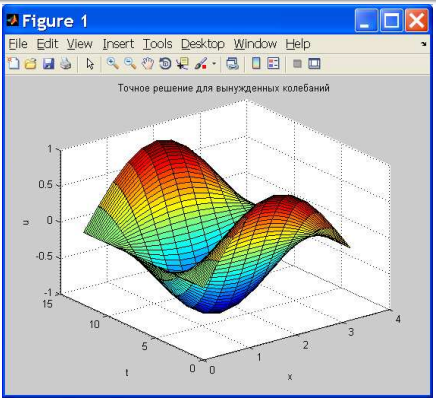 Рисунок 3 – Вынужденные колебания в трёхмерной плоскости Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 Заключение В результате выполнения курсовой работы по расчёту параметров троллейбуса на 90 пассажиров были определены следующие технические характеристики:
массе 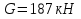
при 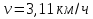
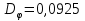 при при 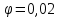
троллейбусом 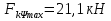
движения 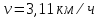
ускорение 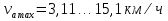
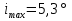 Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 Литература
Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 ПРИЛОЖЕНИЯ ПРИЛОЖЕНИЕ А Таблицы расчёты искусственных характеристик электродвигателя 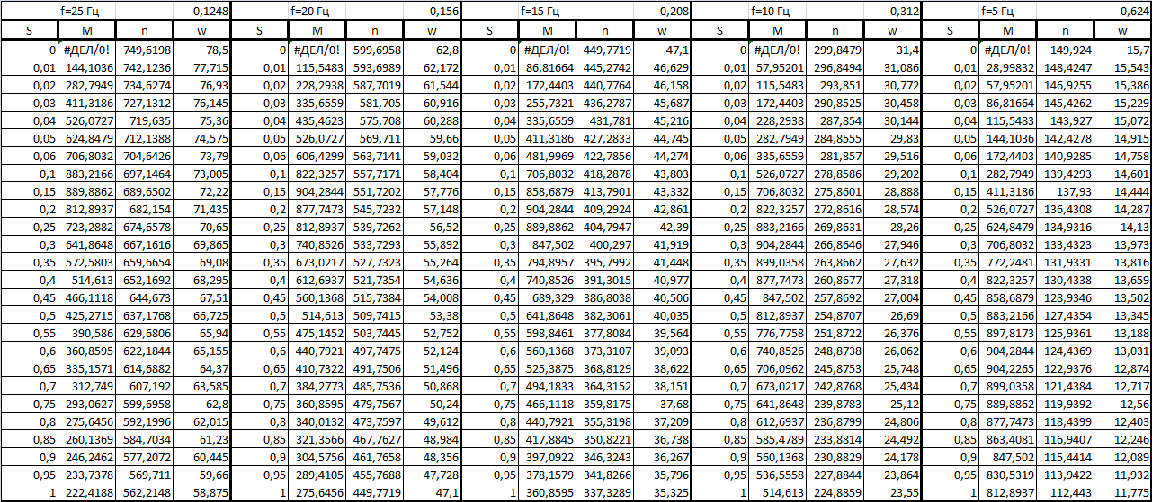 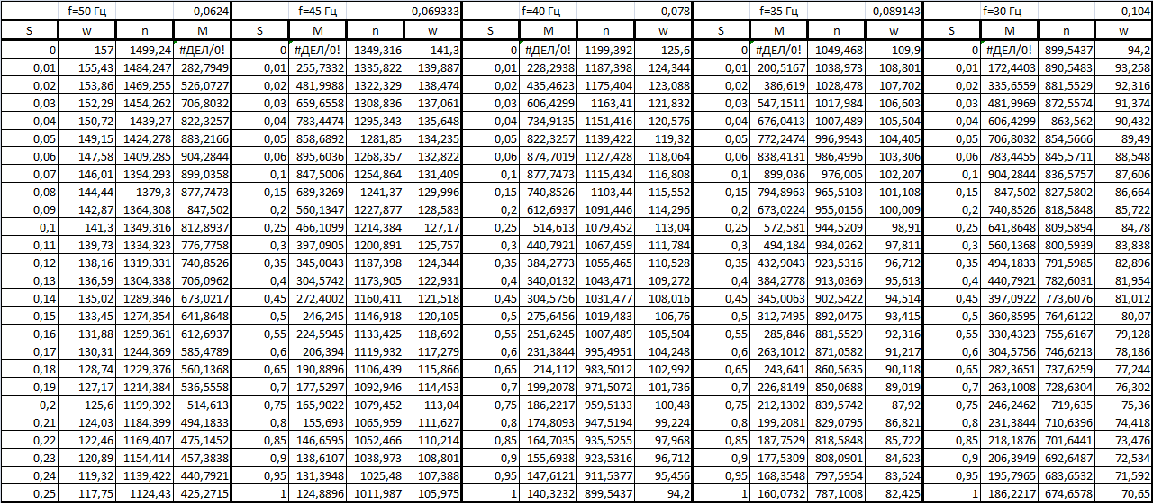 Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 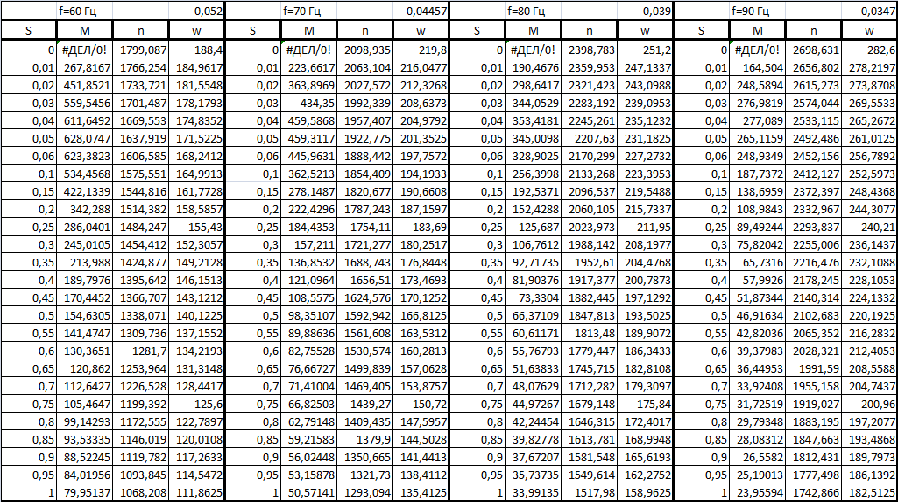 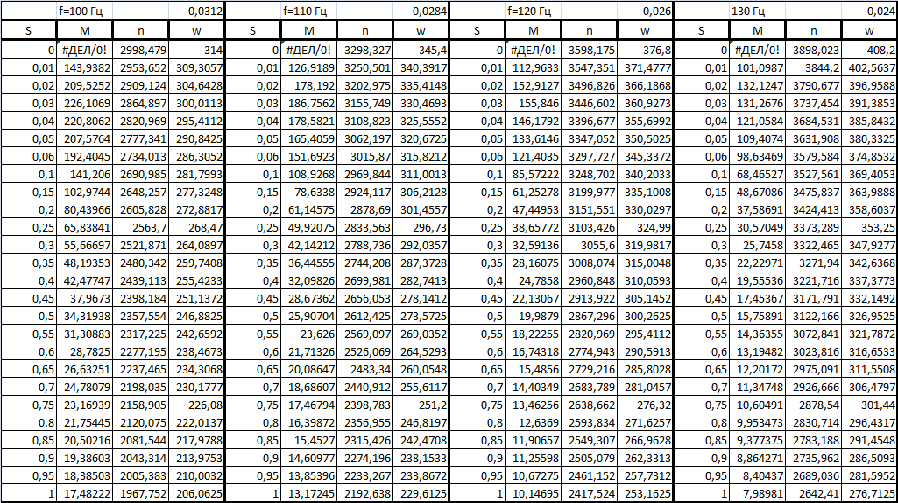 Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 ПРИЛОЖЕНИЕ Б Результаты расчёта изменения вращающего момента ТЭД на основе выбранного закона управления 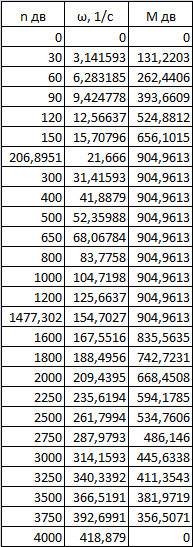 Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 ПРИЛОЖЕНИЕ В Результаты расчёта динамического фактора троллейбуса на 90 пассажиров 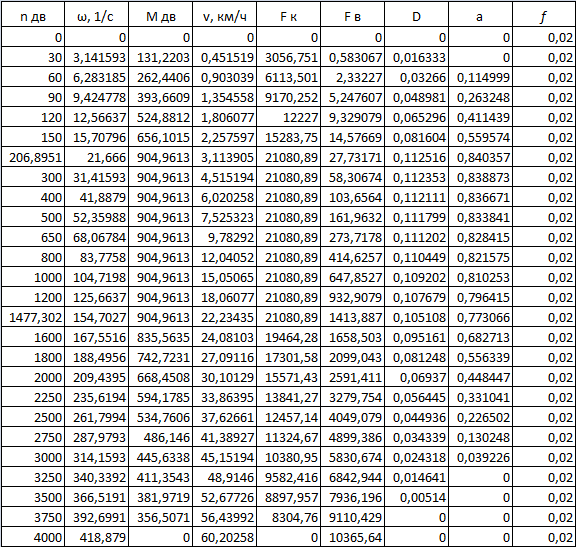 Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 ПРИЛОЖЕНИЕ Г Результаты тягового расчёта троллейбуса на 90 пассажиров 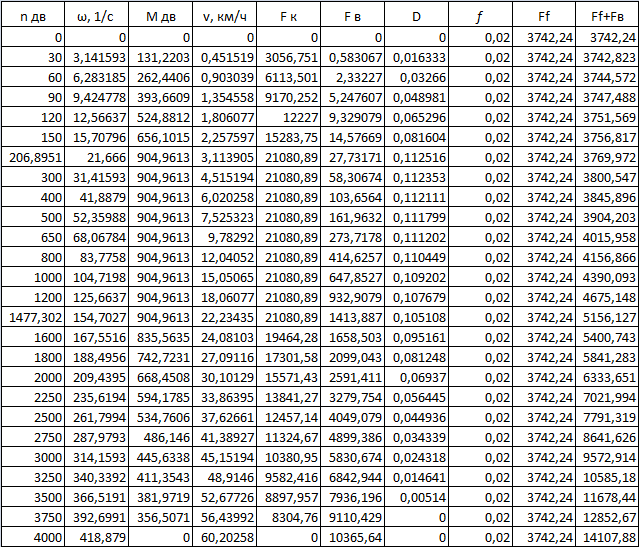 Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 ПРИЛОЖЕНИЕ Д Результаты расчёта ускорения троллейбуса на 90 пассажиров 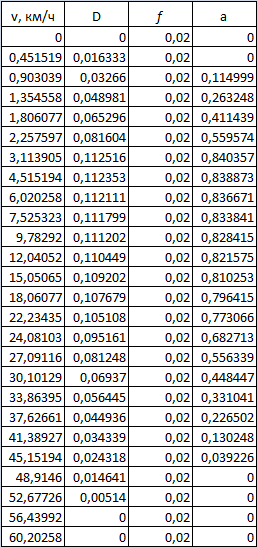 Изм. Лист № докум. Подпись Дата Лист КР – 10110114/09–2017 ПРИЛОЖЕНИЕ Е Результаты расчёта времени и пути разгона троллейбуса на 90 пассажиров 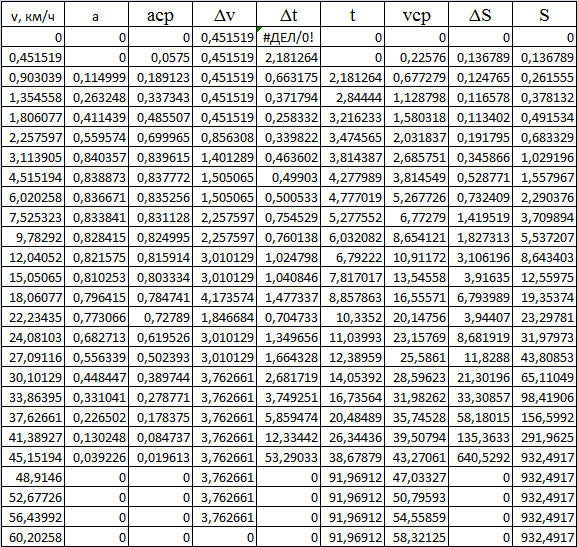 |

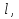
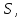
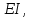
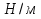
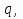
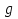
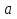
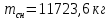
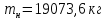
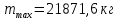
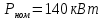
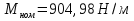
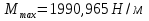
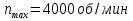
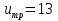
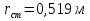
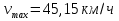
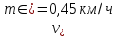
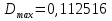
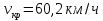
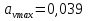
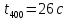
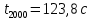
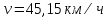 ,
, 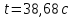
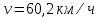 ,
,