Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности. Курсовая работа Сравнение исправленной выборочной дисперсии с ги. Курсовая работа по дисциплине Теория вероятности и математическая статистика
 Скачать 121.3 Kb. Скачать 121.3 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ» 
Курсовая работа
Москва – 2020 СодержаниеВведение 3 Основные сведения о статистической проверке статистических гипотез 3 Основные сведения о сравнении исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности 4 Основная часть 6 Задачи, подтверждающие гипотезу о равенстве исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности 6 Задачи, отвергающие гипотезу о равенстве исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности 8 Решение задач на сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности в профессиональной сфере 10 Список использованных источников и литературы 12 Приложения 13 ВведениеОсновные сведения о статистической проверке статистических гипотезСтатистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Метод использования выборки для проверки истинности статистической гипотезы называется статистическим доказательством истинности выдвинутой гипотезы. Постановка задачи начинается с выдвижения основного утверждения (нулевой или основной гипотезы Н0), причем наряду с выдвинутой гипотезой всегда рассматривают и противоречащую ей гипотезу, которую называют конкурирующей или альтернативной гипотезой Н1. Для проверки нулевой гипотезы используют специально подобранную случайную величину – выборочную статистику, точное или приближенное распределение которой известно. Случайная величина K, построенная по наблюдениям для проверки нулевой гипотезы, называется статистикой критерия. Схема построения критерия такова: все выборочное пространство делится на две взаимодополняющие области – область S отклонения основной гипотезы Н0 и область 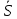 принятия этой гипотезы. Область S, при попадании в которую выборочной точки x = (x1, x2, …, xn) основная гипотеза отклоняется, называется критической. принятия этой гипотезы. Область S, при попадании в которую выборочной точки x = (x1, x2, …, xn) основная гипотеза отклоняется, называется критической.Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают. [4] Основные сведения о сравнении исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупностиПусть генеральная совокупность x имеет нормальное распределение, x1, x2, …, xn – случайная выборка. Пусть 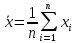 , ,  . Рассматривается нулевая гипотеза H0: . Рассматривается нулевая гипотеза H0: 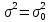 о равенстве известной дисперсии о равенстве известной дисперсии 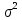 предполагаемому значению предполагаемому значению  при уровне значимости α. при уровне значимости α. Существует несколько правил, выбор которых зависит от вида конкурирующей гипотезы. Рассмотрим их. Правило 1. Пусть конкурирующей гипотезой будет гипотеза H1: 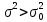 . Критерием в этом случае служит случайная величина . Критерием в этом случае служит случайная величина 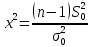 , имеющая распределение x2 с числом степеней свободы k = n - 1. По данной числовой выборке x1, x2, … , xn вычисляется значение x2набл. При уровне значимости α и данному числу степеней свободы k = n – 1 по таблице критических точек распределения x2 находится критическая точка x2кр (α, k). , имеющая распределение x2 с числом степеней свободы k = n - 1. По данной числовой выборке x1, x2, … , xn вычисляется значение x2набл. При уровне значимости α и данному числу степеней свободы k = n – 1 по таблице критических точек распределения x2 находится критическая точка x2кр (α, k).Если x2набл Правило 2. При конкурирующей гипотезе H1:  находят левую критическую точку x2лев.кр (1-α/2, k) и правую x2пр.кр (α/2, k). Если x2лев.кр находят левую критическую точку x2лев.кр (1-α/2, k) и правую x2пр.кр (α/2, k). Если x2лев.кр Правило 3. При конкурирующей гипотезе H1: 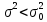 находят критическую точку x2кр (1 - α, k). Если x2набл> x2кр (1 - α, k), то нет оснований отвергнуть нулевую гипотезу. Если x2набл находят критическую точку x2кр (1 - α, k). Если x2набл> x2кр (1 - α, k), то нет оснований отвергнуть нулевую гипотезу. Если x2набл На практике рассматриваемая гипотеза проверяется, если нужно проверить точность приборов, инструментов, станков, методов исследования и устойчивость технологических процессов, ритмичности. Например, если известна допустимая характеристика рассеяния контролируемого размера деталей, изготавливаемых станком-автоматом, равная σ02, а найденная по выборке 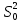 окажется значимо больше, то станок требует наладки. окажется значимо больше, то станок требует наладки.Основная частьЗадачи, подтверждающие гипотезу о равенстве исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупностиЗадача 1. Точность работы станка-автомата проверяется по дисперсии 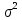 контролируемого размера изделий, которая не должна превышать 0,15. По данным из n = 25 отобранных изделий вычислена оценка дисперсии контролируемого размера изделий, которая не должна превышать 0,15. По данным из n = 25 отобранных изделий вычислена оценка дисперсии  . При уровне значимости α = 0,01 выяснить, обеспечивает ли станок требуемую точность. [2] . При уровне значимости α = 0,01 выяснить, обеспечивает ли станок требуемую точность. [2]Решение. Нулевой гипотезой будет H0: 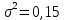 , конкурирующей – H1: , конкурирующей – H1:  . Вычислим значение критерия: . Вычислим значение критерия: 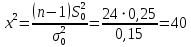 . .По таблице критических точек распределения x2 (Приложение 1 [5]) со степенями свободы k = 24 при уровне значимости α = 0,01, находим x2кр (0,01; 24) = 43. Поскольку x2набл 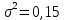 . .Задача 2. Из нормальной генеральной совокупности извлечена выборка объема n = 21 и по ней найдена исправленная выборочная дисперсия S2 = 16,2. Требуется при уровне значимости 0,01 проверить нулевую гипотезу H0: 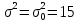 , приняв в качестве конкурирующей гипотезы H1: , приняв в качестве конкурирующей гипотезы H1: . [1] . [1]Решение. Найдем наблюдаемое значение критерия: 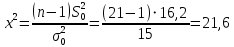 . .По условию, конкурирующая гипотеза имеет вид  , поэтому критическая область – правосторонняя (правило 1). По таблице критических точек распределения, по уровню значимости 0,01 и числу степеней свободы k=n–1=21–1=20 находим критическую точку x2кр (0,01; 20) = 37,6. , поэтому критическая область – правосторонняя (правило 1). По таблице критических точек распределения, по уровню значимости 0,01 и числу степеней свободы k=n–1=21–1=20 находим критическую точку x2кр (0,01; 20) = 37,6.Так как x2набл 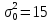 . . Задачи, отвергающие гипотезу о равенстве исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупностиЗадача 1. Ритмичность работы кассира Сбербанка по приему коммунальных платежей определяется дисперсией времени обслуживания клиентов, которая не должна превышать величины  мин2. Результаты 30 наблюдений за работой нового кассира приведены в таблице: [3] мин2. Результаты 30 наблюдений за работой нового кассира приведены в таблице: [3]
Проверим нулевую гипотезу о допустимой ритмичности работы новичка при уровне значимости 0,05.
 . .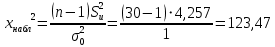 . .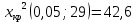 . . => Нулевая гипотеза о равенстве дисперсий опровергнута, значит, новый кассир пока еще не вошел в требуемый ритм работы. => Нулевая гипотеза о равенстве дисперсий опровергнута, значит, новый кассир пока еще не вошел в требуемый ритм работы.Задача 2. Партия изделий принимается, если дисперсия контролируемого размера значимо не превышает 0,2. Исправленная выборочная дисперсия, найденная по выборке объема n = 121, оказалась равной 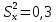 . Можно ли принять партию при уровне значимости 0,01? [1] . Можно ли принять партию при уровне значимости 0,01? [1]Решение. Нулевая гипотеза H0: 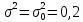 . Конкурирующая гипотеза H1: . Конкурирующая гипотеза H1: 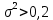 . .Найдем наблюдаемое значение критерия:  . .Конкурирующая гипотеза имеет вид 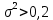 , следовательно, критическая область правосторонняя. Поскольку в таблице критических точек распределения не содержатся числа степеней свободы k = 120, найдем критическую точку приближенно из равенства Уилсона-Гильферти: , следовательно, критическая область правосторонняя. Поскольку в таблице критических точек распределения не содержатся числа степеней свободы k = 120, найдем критическую точку приближенно из равенства Уилсона-Гильферти: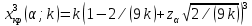 . .Найдем предварительно 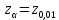 из равенства Ф ( из равенства Ф (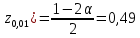 . .По таблице функции Лапласа, используя линейную интерполяцию, находим: 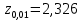 . Подставив k = 120, . Подставив k = 120,  в формулу Уилсона - Гильферти, получим в формулу Уилсона - Гильферти, получим 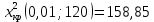 . Так как . Так как  – нулевую гипотезу отвергаем. Партию принять нельзя. – нулевую гипотезу отвергаем. Партию принять нельзя.Решение задач на сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности в профессиональной сфере
Задача 1. Компания I-TECO оценивает эффективность используемых информационных систем в компаниях, используя в качестве показателя эффективности отношение количества верно проведенных операций к количеству всех операций, совершенных ИС. Для оценки ИС в Альфа-банке IT-аналитики провели эксперимент, в ходе которого было установлено, что дисперсия результатов измерений составляет 0,005. Можно ли утверждать, что существующая в банке ИС эффективно выполняет свои функциональные опции и не требует замены? Проверить нулевую гипотезу H0: 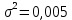 при уровне значимости α = 0,1 и при конкурирующей гипотезе H1: при уровне значимости α = 0,1 и при конкурирующей гипотезе H1:  . .Решение. Выборочное значение дисперсии, вычисленное по объему выборки n = 10, оказалось равным 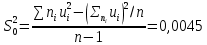 . . Найдем наблюдаемое значение критерия: 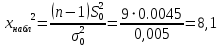 . .Так как конкурирующая гипотеза H1: 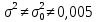 , то найдем левую критическую точку x2лев.кр (1-α/2, k) и правую x2пр.кр (α/2, k). , то найдем левую критическую точку x2лев.кр (1-α/2, k) и правую x2пр.кр (α/2, k).x2лев.кр (1-α/2, k) = (0,95; 9) = 3,33. x2пр.кр (α/2, k) = (0,05; 9) = 16,9. Получаем, что x2лев.кр Таким образом, IT-аналитики пришли к выводу о высокой эффективности существующей ИС в банке. Список использованных источников и литературыГмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие – 11-е изд., перераб. -Москва: Высшее образование, 2008. – 404 с. – (Основы наук). Математическая статистика. Примеры и задачи: учебное пособие/ М.Ю. Васильчик, А.П. Ковалевский, И.М. Пупышев и др. – Новосибирск: Изд-во НГТУ, 2011 – 84 с. Лекции.Ком [Электронный ресурс]. – Электрон. текстовые дан. – [б.и.], 23.12.2014. - Режим доступа: https://lektsii.com// свободный. Теория вероятностей и математическая статистика. Фадеева Л.Н., Лебедев А.В. М.: ЭКСПО, 2010. – 496 с. ПриложенияПриложение 1 – Таблица критических точек распределения x2.  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
