Курсач. приписка. Курсовая работа по дисциплине Введение в информационные технологии
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
2)Расчёт аппроксимации и построение графиков MS Excel2.1)Расчет аппроксимацииСначала проведем расчеты, используя средства табличного процессора MS Excel. Данные представлены на Рисунке 1 и Рисунке 2. 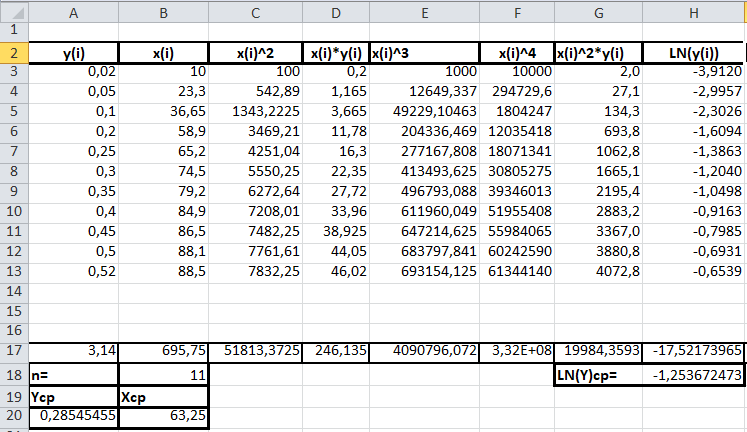 Рис.1. Вычисление вспомогательных сумм и средних значений 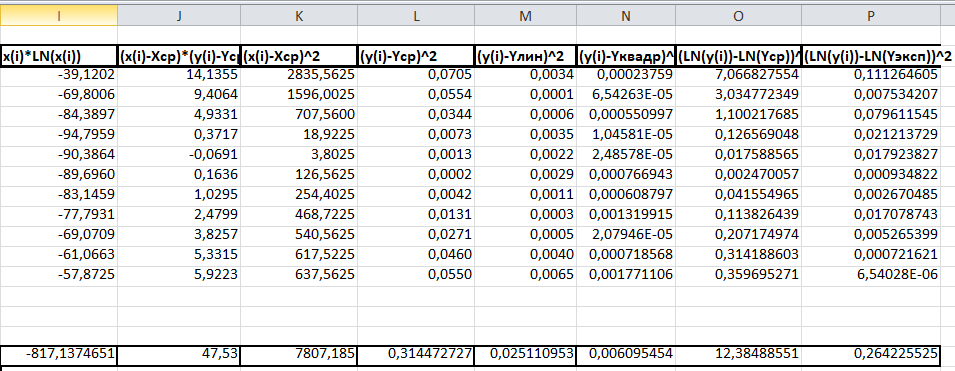 Рис.2. Вычисление вспомогательных сумм и средних значений Пояснения к расчетам: Шаг 1. В ячейки A3:A16 заносим значения y(i). Шаг 2. В ячейки B3:B16 заносим значения x(i). Шаг 3. В ячейку C3 вводим формулу =B3^2. Шаг 4. В ячейки C4:C16 эта формула копируется. Шаг 5. В ячейку D3 вводим формулу =B3*A3. Шаг 6. В ячейки D4:D16 эта формула копируется. Шаг 7. В ячейку E3 вводим формулу =B3^3. Шаг 8. В ячейки E4:E16 эта формула копируется. Шаг 9. В ячейку F3 вводим формулу =B3^4. Шаг 10. В ячейки F4:F16 эта формула копируется. Шаг 11. В ячейку G3 вводим формулу =B3^2*A3. Шаг 12. В ячейки G4:G16 эта формула копируется. Шаг 13. В ячейку H3 вводим формулу =LN(A3) Шаг 14. В ячейки H4:H16 эта формула копируется. Шаг 15. В ячейку I3 вводим формулу =B3*LN(A3). Шаг 16. В ячейки I4:I16 эта формула копируется. Последующие шаги делаем с помощью автосуммирования ∑ . Шаг 17. В ячейку A17 вводим формулу =СУММ(A3:A16). Шаг 18. В ячейку B17 вводим формулу =СУММ(B3:B16). Шаг 19. В ячейку C17 вводим формулу =СУММ(C3:C16). Шаг 20. В ячейку D17 вводим формулу =СУММ(D3:D16). Шаг 21. В ячейку E17 вводим формулу =СУММ(E3:E16). Шаг 22. В ячейку F17 вводим формулу =СУММ(F1:F16). Шаг 23. В ячейку G17 вводим формулу =СУММ(G3:G16). Шаг 24. В ячейку H17 вводим формулу =СУММ(H3:H16). Шаг 25. В ячейку I17 вводим формулу =СУММ(I3:I16). Далее вычисляем средние значения: Шаг 26. В ячейку B18 вводим формулу =СЧЁТ(B3:B16). Шаг 27. В ячейку A19 вводим формулу =A17/$B$18. Шаг 28. В ячейку B19 вводим формулу =B17/$B$18. Шаг 29. В ячейку H18 вводим формулу =H17/$B$18. Продолжаем заполнение таблицы (рис, 3). Шаг 30. В ячейку J3 вводим формулу =(B3-$B$19)*(A3-$A$19). Шаг 31. В ячейки J4:J16 эта формула копируется. Шаг 32. В ячейку K3 вводим формулу =(B3-$B$19)^2. Шаг 33. В ячейки K4:K16 эта формула копируется. Шаг 34. В ячейку L3 вводим формулу =(A3-$A$19)^2. Шаг 35. В ячейки L4:L16 эта формула копируется. Последующие шаги делаем с помощью автосуммирования ∑ . Шаг 36. В ячейку J17 вводим формулу =СУММ(J3:J16). Шаг 37. В ячейку K17 вводим формулу =СУММ(K3:K16). Шаг 38. В ячейку L17 вводим формулу =СУММ(L3:L16). На рисунке 3 представлены расчеты для линейной аппроксимации  Рис.3. Фрагмент рабочего листа MS Excel для линейной аппроксимации Шаг 39. В ячейку A22 вводим формулу =$B$18. Шаг 40. В ячейку B22 вводим формулу =B17. Шаг 41. В ячейку A23 вводим формулу =B17. Шаг 42. В ячейку B23 вводим формулу =C17. Шаг 43. В ячейку C22 вводим формулу =A17. Шаг 44. В ячейку C23 вводим формулу =D17. Шаг 45. Выделяем ячейки A26:B27 и вводим формулу {=МОБР(A22:B23)}. Шаг 46. Выделяем ячейки E26:E27 и вводим формулу {=МУМНОЖ(A26:B27;C22:C23)}. Шаг 47. В ячейку E24 вводим формулу =J17/(K17*L17)^(1/2). Шаг 48. В ячейку M3 вводим формулу =(A3-($E$26+$E$27*B3))^2. 19 Шаг 49. В ячейки M4:M16 эта формула копируется. Шаг 50. В ячейку M17 вводим формулу =СУММ(M3:M16). Шаг 51. В ячейку E25 вводим формулу =1-M17/L17. Шаг 52. В ячейку B29 вводим число 5,12 11 =df и 1222 =−= ndf в табл. 46 из приложения 1). Шаг 53. В ячейку B30 вводим формулу =E25*(B18-2)/(1-E25). Шаг 54. В ячейку B31 вводим формулу =M17/(B18-2). Шаг 55. В ячейку B32 вводим формулу =((B31*C17)/(B18*K17))^(1/2). Шаг 56. В ячейку B33 вводим формулу =(B31/K17)^(1/2). Шаг 57. В ячейку C30 вводим формулу =ЕСЛИ(B30>B29;"Уравнение значимо";"Уравнение не значимо"). Шаг 58. В ячейку D31 вводим число 1,8125 Шаг 59. В ячейку D32 вводим формулу =ABS(E26)/B32. Шаг 60. В ячейку D33 вводим формулу =ABS(E27)/B33. Шаг 61. В ячейку F32 вводим формулу =ЕСЛИ(D32>$D$31;"значим";"не значим"). Шаг 62. В ячейку F33 вводим формулу =ЕСЛИ(D33>$D$31;"значим";"не значим"). При этом согласно критерию Фишера – Снедекора, уравнение линейной регрессии значимо и коэффициент этого уравнения согласно критерия Стьюдента тоже значим. Расчёты для квадратичной аппроксимации представлены на рисунке 4. 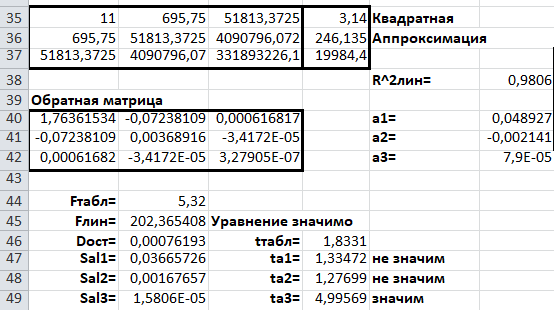 Рис.4. Фрагмент рабочего листа MS Excel для квадратичной аппроксимации Шаг 63. В ячейку A35 вводим формулу =$B$18. Шаг 64. Шаг 86. В ячейку A36 вводим формулу =B17. Шаг 65. Шаг 88. В ячейку A37 вводим формулу =C17. Шаг 66. В ячейку B35 вводим формулу =B17. Шаг 67 В ячейку B36 вводим формулу =C17. Шаг 68 В ячейку B37 вводим формулу =E17. Шаг 69. В ячейку C35 вводим формулу =C17. Шаг 70. В ячейку C36 вводим формулу =E17. Шаг 71. В ячейку C37 вводим формулу =F17. Шаг 72. В ячейку D35 вводим формулу =A17. Шаг 73. В ячейку D36 вводим формулу =D17. Шаг 74. В ячейку D37 вводим формулу =G17. Шаг 75. Выделяем ячейки A40:C42 и вводим формулу {=МОБР(A35:C37)}. Шаг 76. Выделяем ячейки F40:F42 и вводим формулу { =МУМНОЖ(A40:C42;D35:D37)}. Шаг 77. В ячейку N3 вводим формулу =(A3-($F$40+$F$41*B3+$F$42*B3^2))^2. Шаг 78. В ячейки N4:N16 эта формула копируется. 21 Шаг 79. В ячейку N17 вводим формулу =СУММ(N3:N16). Шаг 80. В ячейку F38 вводим формулу =1-N17/L17. Шаг 81. В ячейку B44 вводим число 5,32 Шаг 82. В ячейку B45 вводим формулу =F38*(B18-3)/(2*(1-F38)). Шаг 83. В ячейку B46 вводим формулу =N17/(B18-3) Шаг 84. В ячейку B47 вводим формулу =((N17/($B$18-3))*A40)^(1/2). Шаг 85. В ячейку B48 вводим формулу =((N17/($B$18-3))*B41)^(1/2). Шаг 86. В ячейку B49 вводим формулу =((N17/($B$18-3))*C42)^(1/2). Шаг 87. В ячейку C45 вводим формулу =ЕСЛИ(B45>B44;"Уравнение значимо";"Уравнение не значимо"). Шаг 88. В ячейку C45 вводим формулу Шаг 89. В ячейку D46 вводим число 1,8331 Шаг 90. В ячейку D47 вводим формулу =ABS(F40)/B47. Шаг 91. В ячейку D48 вводим формулу =ABS(F41)/B48. Шаг 92. В ячейку D49 вводим формулу =ABS(F42)/B49. Шаг 93. В ячейку F47 вводим формулу =ЕСЛИ(D47>$D$46;"значим";"не значим"). Шаг 94. В ячейку F48 вводим формулу =ЕСЛИ(D48>$D$46;"значим";"не значим"). Шаг 95. В ячейку F49 вводим формулу =ЕСЛИ(D49>$D$46;"значим";"не значим"). Согласно критерию Фишера – Снедекора, уравнение квадратичной регрессии (24) значимо. Два коэффициента этого уравнения 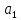 и и 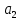 согласно критерию Стьюдента не значимы, а третий коэффициент согласно критерию Стьюдента не значимы, а третий коэффициент 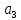 , - значим. , - значим.Расчёты для экспоненциальной аппроксимации представлены на рисунке 5. 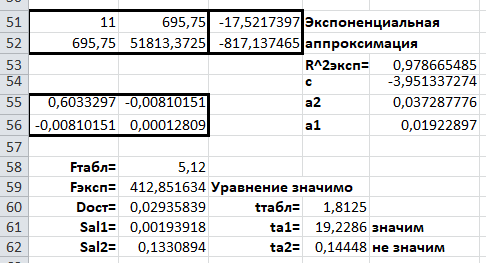 Рис.5. Фрагмент рабочего листа MS Excel для экспоненциальной аппроксимации Шаг 92. В ячейку А51 вводим формулу =$B$18. Шаг 93. В ячейку В51 водим формулу =В17. Шаг 94. В ячейку А52 вводим формулу =В17. Шаг 95. В ячейку В52 вводим формулу =С17. Шаг 96 В ячейку С51 вводим формулу =Н17. Шаг 97. В ячейку С51 вводим формулу =I17. Шаг 98. Выделяем ячейку А55:В56 и вводим формулу {=МОБР(А51:В52)}. Шаг 99. Выделяем ячейку Е54:Е55 и вводим формулу {=МУМНОЖ(А55:В56;С51:С52)}. Шаг 100. В ячейку Е56 вводим формулу =EXP(Е54). Шаг 101. В ячейку Е53 вводим формулу =1-P17/O17. Шаг 102. В ячейку В58 вводим формулу =В29. Шаг 103. В ячейку В59 вводим формулу =E53*(B18-2)/(1-E56). Шаг 104. В ячейку В60 вводим формулу =Р17/(В18-2)). Шаг 105. В ячейку В61 вводим формулу =(P17/(($B$18-2)*K17))^(1/2) Шаг 106. В ячейку В62 вводим формулу =((P17*C17)/(($B$18-2)*$B$18*K17))^(1/2). Шаг 107. В ячейку С59 вводим формулу =ЕСЛИ(В59<В59;”значим”;”не значим”). Шаг 108. В ячейку D60 вводим формулу =D31. Шаг 109. В ячейку D61 вводим формулу =ABS(E55)/B61. Шаг 110. В ячейку D62 вводим формулу =ABS(E56)/B62. Шаг 111. В ячейку F61 вводим формулу =ЕСЛИ(D58<$D$60;”значим”;”не значим”). Шаг 112. В ячейку F62 вводим формулу =ЕСЛИ(D62<$D$60;”значим”;”не значим”). Согласно критерию Фишера – Снедекора, уравнение экспоненциальной регрессии значимо. Первый коэффициент этого уравнения, согласно критерию Стьюдента, значим, второй - нет. Таким образом уравнения аппроксимаций имеют вид: Для линейной: y = 0,0061x - 0,0996 Для квадратичной: y = 8E-05x2 - 0,0021x + 0,0489 Для экспоненциальной: y = 0,0192e0,0373x |
